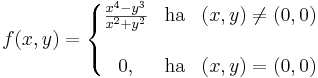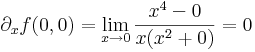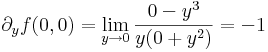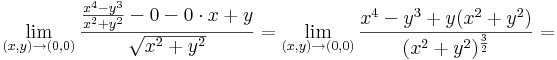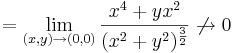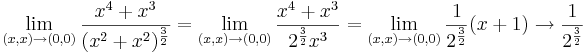Matematika A2a 2008/11. gyakorlat
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) (→Totális és folytonos parciális deriválhatóság) |
||
| 8. sor: | 8. sor: | ||
0, & \mathrm{ha} & (x,y)=(0,0) | 0, & \mathrm{ha} & (x,y)=(0,0) | ||
\end{matrix}\right.</math> | \end{matrix}\right.</math> | ||
| − | függvény az origóban? | + | függvény az origóban? Folyt. diff.-e, létezik-e a gradiens, létezik-e a Jacobi-mátrix ott? |
:<math>\partial_xf(0,0)=\lim\limits_{x\to 0}\frac{x^4-0}{x(x^2+0)}=0</math> | :<math>\partial_xf(0,0)=\lim\limits_{x\to 0}\frac{x^4-0}{x(x^2+0)}=0</math> | ||
| 19. sor: | 19. sor: | ||
ugyanis | ugyanis | ||
:<math>\lim\limits_{(x,x)\to (0,0)}\frac{x^4+x^3}{(x^2+x^2)^{\frac{3}{2}}}=\lim\limits_{(x,x)\to (0,0)}\frac{x^4+x^3}{2^{\frac{3}{2}}x^3}=\lim\limits_{(x,x)\to (0,0)}\frac{1}{2^{\frac{3}{2}}}(x+1)\to \frac{1}{2^{\frac{3}{2}}}</math> | :<math>\lim\limits_{(x,x)\to (0,0)}\frac{x^4+x^3}{(x^2+x^2)^{\frac{3}{2}}}=\lim\limits_{(x,x)\to (0,0)}\frac{x^4+x^3}{2^{\frac{3}{2}}x^3}=\lim\limits_{(x,x)\to (0,0)}\frac{1}{2^{\frac{3}{2}}}(x+1)\to \frac{1}{2^{\frac{3}{2}}}</math> | ||
| + | Tehát nem folyt diff, mert ha az lenne, akkor deriválható is lenne (egy környzetben létezik a derivált!). Jacobi van, gradiens nincs, mert az a differenciál leképezés skalárinvariánssa lenne ( az az ''m'' vektor, melyet az ''Ax''=''m''<math>\cdot</math>''x'' definiál, de nincs alkalmas ''A'', így nincs alkalmas ''m''). | ||
<center> | <center> | ||
{| class="wikitable" style="text-align:center" | {| class="wikitable" style="text-align:center" | ||
A lap 2009. május 14., 21:32-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Totális és folytonos parciális deriválhatóság
Deriválható-e az
függvény az origóban? Folyt. diff.-e, létezik-e a gradiens, létezik-e a Jacobi-mátrix ott?
A deriválhatóság:
ugyanis
Tehát nem folyt diff, mert ha az lenne, akkor deriválható is lenne (egy környzetben létezik a derivált!). Jacobi van, gradiens nincs, mert az a differenciál leképezés skalárinvariánssa lenne ( az az m vektor, melyet az Ax=m x definiál, de nincs alkalmas A, így nincs alkalmas m).
x definiál, de nincs alkalmas A, így nincs alkalmas m).
| 10. gyakorlat | 12. gyakorlat |