Matematika A2a 2008/2. gyakorlat
Mozo (vitalap | szerkesztései) (→Határérték) |
Mozo (vitalap | szerkesztései) (→Határérték) |
||
| 132. sor: | 132. sor: | ||
'''8.''' HF. Hol létezik határértéke az | '''8.''' HF. Hol létezik határértéke az | ||
:<math>f(x,y)=\dfrac{xy^3}{x^2+y^6}</math> | :<math>f(x,y)=\dfrac{xy^3}{x^2+y^6}</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
függvénynek? | függvénynek? | ||
A lap jelenlegi, 2017. február 19., 18:53-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Tartalomjegyzék |
Kétváltozós függvények szemléltetése
a) 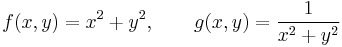
b) 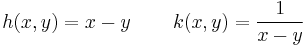
Ábrázoljuk őket a wolfram alfán:
[wolframalpha 3D Plots|http://www.wolframalpha.com/examples/PlottingAndGraphics.html]
Ezek (x,y,z) koordinátarendszerbeli z=f(x,y) felülettel ábrázolva hengerszimmetrikusak, érdemes az
polárkoordináta transzformációval átírni, ebben 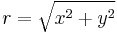 a z-tengelytől mért távolság, és az első és második (majd a második és harmadik síknegyedben):
a z-tengelytől mért távolság, és az első és második (majd a második és harmadik síknegyedben): 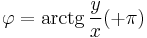
Innen: 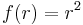 z körül körbeforgatott parabola (forgási paraboloid)
z körül körbeforgatott parabola (forgási paraboloid)
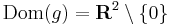 és
és 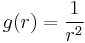 másodfokú hiperbola körbeforgatva.
másodfokú hiperbola körbeforgatva.
Mindkettő szintvonalai körök.
b) h(x,y)=z=x-y egy sík egyenlete, szintvonalai: c=x-y, y=x-c egyenesek.
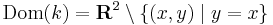 szintén egyenesek a szintvonalak:
szintén egyenesek a szintvonalak: 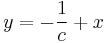 .
.
Határérték
Def. Tegyük fel, hogy az 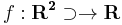 függvény értelmezési tartományának (x0,y0) torlódási pontja. Azt mondjuk, hogy f-nek létezik határértéke az (x0,y0) pontban, és ez az A szám, ha
függvény értelmezési tartományának (x0,y0) torlódási pontja. Azt mondjuk, hogy f-nek létezik határértéke az (x0,y0) pontban, és ez az A szám, ha
- minden ε>0-ra létezik δ>0, hogy
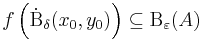
Ilyenkor 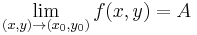 -t vagy
-t vagy 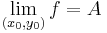 -t írunk.
-t írunk.
Rendőrelv. Legyen 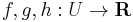 és
és 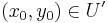 . Ha van olyan δ>0, hogy minden
. Ha van olyan δ>0, hogy minden 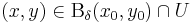 -ra
-ra
és 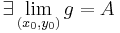 és
és 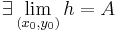 , akkor
, akkor
Határérték nem létezésének jellemzése. Tegyük fel, hogy az 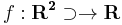 függvény értelmezési tartományának (x0,y0) torlódási pontja. f-nek nem létezik véges határértéke az (x0,y0) pontban, pontosan akkor, ha léteznek olyan
függvény értelmezési tartományának (x0,y0) torlódási pontja. f-nek nem létezik véges határértéke az (x0,y0) pontban, pontosan akkor, ha léteznek olyan 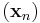 és
és 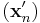 sorozatok, hogy
sorozatok, hogy 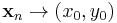 és
és 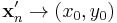 , de
, de 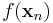 vagy
vagy 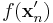 nem konvergensek, vagy ha igen, akkor
nem konvergensek, vagy ha igen, akkor 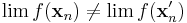 .
.
Folytonosság. Legyen 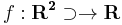 és
és 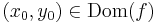 . Azt mondjuk, hogy f folytonos az (x0,y0) pontban, ha
. Azt mondjuk, hogy f folytonos az (x0,y0) pontban, ha
- minden ε>0-ra létezik δ>0, hogy
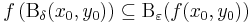
Ha 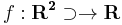 olyan, hogy
olyan, hogy 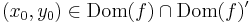 , akkor
, akkor 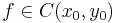 pontosan akkor, ha
pontosan akkor, ha 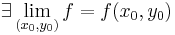 .
.
1. Hol létezik határértéke az
függvénynek? ("A félév függvénye.")
- Megoldás. Világos, hogy a polárkoordináta transzformációval az r kiesik és csak φ-től függ. Ezért érdemes a (0,0) pontot több irnyból, sugárirányba megközelíteni, általánosan az y = mx egyenes mentén:
- Vagyis m=0-ra ez 0-t, m=1-re ez 1/2-et ad. Eszerint nincs a (0,0)-ban határérték, mert van két különböző határértékű függvényértéksorozat, miközben a sorozatokkal a (0,0)-ba tartunk.
- Megoldás. Világos, hogy a polárkoordináta transzformációval az r kiesik és csak φ-től függ. Ezért érdemes a (0,0) pontot több irnyból, sugárirányba megközelíteni, általánosan az y = mx egyenes mentén:
2. Hol létezik határértéke az
függvénynek?
MO.: Mindenütt folytonos, ahol értelmezve van, de nincs hatérértéke másutt, ugyanis:
Polárkoordinátákra áttérve:
ami független r-től, tehát pl a (0,0)-beli határérték attól függ, hogy hogy közelítünk a 0-hoz.
3. Hol létezik határértéke az
függvénynek?
4. Hol létezik határértéke az
függvénynek? (Használjuk az ![|f(x,y)|\leq g(r)\xrightarrow[r\to 0]\, 0](/upload/math/8/3/d/83d45d97d88d983b42cddea534631489.png) , akkor
, akkor ![f(x,y)\xrightarrow[(x,y)\to (0,0)]\,0](/upload/math/e/e/1/ee1b25786ab71d9147e70c5bd1ed4996.png) "rendőrelvet", ahol
"rendőrelvet", ahol 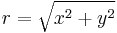 , vagy vegyük észre a "félév függvényét".)
, vagy vegyük észre a "félév függvényét".)
- 1. megoldás (polártranszf.). x = r
 cos(φ), y = r
cos(φ), y = r sin(φ):
sin(φ):
- Ami 0-hoz tartó szor korlátos, amennyiben (x,y)
 (0,0) ( (x,y) tart 0 esetén r tart a 0-hoz, a trigonometrikusak megmindenhogy nézve korlátosak), azaz a határérték 0.
(0,0) ( (x,y) tart 0 esetén r tart a 0-hoz, a trigonometrikusak megmindenhogy nézve korlátosak), azaz a határérték 0.
- 2. megoldás (mértani-négyzetes közepek). |x||y|
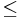 (x2 + y2)/2. Emiatt:
(x2 + y2)/2. Emiatt:
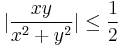
- Ha (x,y)
 (0,0), akkor persze |x|
(0,0), akkor persze |x|  0 és a többi tényező szorzata korlátos (éspedig -1/2 és 1/2 közötti), hiszen a hányados kisebb egyenlő 1. Ezért a határérték 0.
0 és a többi tényező szorzata korlátos (éspedig -1/2 és 1/2 közötti), hiszen a hányados kisebb egyenlő 1. Ezért a határérték 0.
- 1. megoldás (polártranszf.). x = r
5. Hol létezik határértéke az
függvénynek? (Használjuk az "x2 = y4" trükköt! 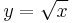 )
)
6. Mi a határértéke rögzített φ-re?
függvénynek?
7. Hol létezik határértéke az
függvénynek? (Vegyük észre a "félév függvényét", vagy írjuk fel a számtani és mértani közép közötti egyenlőtlenséget a nevező tagjaira.)
8. HF. Hol létezik határértéke az
függvénynek?
IMSc Kiegészítés
Sorozatok konvergenciája normált térben
Azt mondjuk, hogy az (an) sorozat konvergens az (E, ||.||) normált térben és határértéke a u ∈ E pont, ha
Komponenssorozatok Rm-ben
(an):Z+  Rm akkor és csak akkor konvergens, ha komponenssorozatai konvergensek.
Rm akkor és csak akkor konvergens, ha komponenssorozatai konvergensek.
Ugyanis, ha konvergens, akkor a maximumnormában is konvergens, azaz ε > 0-hoz létezik N természetes szám, hogy minden n > N természetes számra
amiből következik, hogy minden n> N-re egyenként:
azaz mindegyik komponenessorozata konvergens.
Megfordítva. Tegyük fel, hogy tetszőleges ε > 0-ra léteznek { Ni} (i=1...m) természetes számok, hogy:
ha tehát N= max{Ni}, akkor minden n > N-re
azaz
-
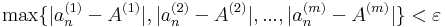 ,
,
azaz a sorozat a maximumnormában konvergál az A = ( A(1) , A(2), ... , A(m)) koordinátájú ponthoz, így az euklideszi normában is.
Példák
1. R2-ben.
Két hasznos dologot jegyezzünk meg:
Tétel Rm-ben minden norma ekvivalens, azaz ugyanazokat a nyílt halmazokat határozza meg. (Tehát, mindegy melyiket használjuk, a nyílt, zárt halmazok topológiai fogalmak (innen pedig a konvergencia is) ugyanaz lesz.
2. B[a,b]-ben.
Legyen B[a,b] a korlátos és zárt [a,b] intervallumon értelmetezett korlátos függvények sorozata. Ebben a térben a távolságot a szuprémumnormából származtatjuk:
azaz gyakorlatilag a "legnagyobb függvényérték különbség". Ekkor egy pont, azaz egy függvény ε sugarú környezete egy 2ε vastag szimmetrikus sáv a függvény grafikonja körül.
2.1. B[-1000,+1000]-ben az
sorozat (függvénysorozat) konvergens a szuprémumnormában. Ezt az előadás alapján úgy fog nevezni, hogy egyenletesen konvergens.
2. B[-2,+2]-ben a páratlan gyökkitevőjű gyökfüggvények függvénysorozata
nem konvergens a szuprémumnormában(!). Az előadáson azt mondjuk majd, hogy nem egyenletesen konvergens. Viszont mint függvénysorozat pontonként konvergens lesz és a szignumfüggvényhez mint hatérfüggvényhez tart.
3. 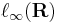 Ez a korlátos sorozatok tere. Itt a
Ez a korlátos sorozatok tere. Itt a
sorozatnak nincs konvergens részsorozata. Ez azért van, mert a sorozat bármely két különböző tagjának különbsége 1, így akárhogy is veszünk egy részsorozatát, az nem lesz Cauchy-sorozat, tehát konvergens sem lehet.
| 1. gyakorlat | 3. gyakorlat |
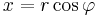
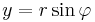
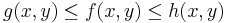
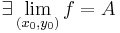
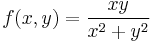
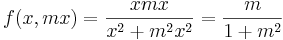
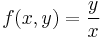
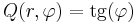
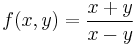
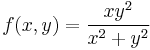
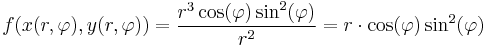
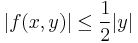
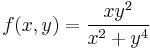
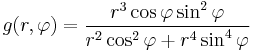
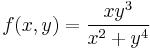
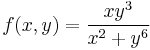

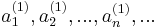
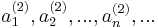

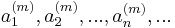
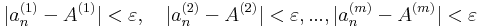
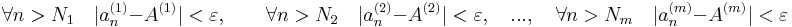
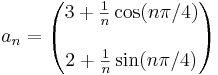
![||f-g||_\infty=\sup \mathrm{Ran}(|f-g|)\}=\sup\{|f(x)-g(x)|\;:\; x\in [a,b]\}](/upload/math/7/f/3/7f3273f1aaf2cf0fabc0567f1390c248.png)
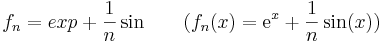
![f_n=\sqrt[2n+1]{.\;}\quad\quad (f_n(x)=\sqrt[2n+1]{x})](/upload/math/6/8/1/68142b19ef9f58a8e151b2ea4973d681.png)