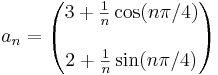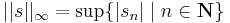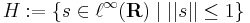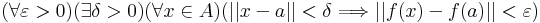Matematika A2a 2008/2. gyakorlat

A MathWikiből
(Változatok közti eltérés)
(→Sorozatok konvergenciája normált térben)
1. sor: 1. sor:
 
:''Ez az szócikk a [[Matematika A2a 2008]] alszócikke.''
 
:''Ez az szócikk a [[Matematika A2a 2008]] alszócikke.''
  
−
==Sorozatok konvergenciája normált térben==  
+
==Sorozatok konvergenciája normált térben==
 +
Azt mondjuk, hogy az (<math>a_n</math>) sorozat '''konvergens''' az (''E'', ||.||) normált térben és határértéke a ''u'' &isin; ''E'' pont, ha
 +
:<math>\forall \varepsilon >0\quad \exists N_{\varepsilon} \in\mathbf{Z}^+\quad\forall n\in\mathbf{Z}^+\quad\quad n>N_\varepsilon\quad\Rightarrow\quad a_n\in B_\varepsilon^{||.||}(u)</math>
 +
===Példák===
 +
'''1.''' '''R'''<sup>2</sup>-ben.
 +
:<math>a_n=\left(\begin{matrix}3+\frac{1}{n}\cos(n\pi/4)\\ \\2+\frac{1}{n}\sin(n\pi/4)\end{matrix}\right)</math>
  
 
==Bolzano-Weierstrass-tételkör==
 
==Bolzano-Weierstrass-tételkör==

A lap 2008. február 17., 17:13-kori változata

Ez az szócikk a Matematika A2a 2008 alszócikke.

Tartalomjegyzék

Sorozatok konvergenciája normált térben

Azt mondjuk, hogy az (an) sorozat konvergens az (E, ||.||) normált térben és határértéke a u ∈ E pont, ha

\forall \varepsilon >0\quad \exists N_{\varepsilon} \in\mathbf{Z}^+\quad\forall n\in\mathbf{Z}^+\quad\quad n>N_\varepsilon\quad\Rightarrow\quad a_n\in B_\varepsilon^{||.||}(u)

Példák

1. R2-ben.

a_n=\left(\begin{matrix}3+\frac{1}{n}\cos(n\pi/4)\\ \\2+\frac{1}{n}\sin(n\pi/4)\end{matrix}\right)

Bolzano-Weierstrass-tételkör

Kompakt egy K halmaz, ha minden nyílt halmazrendszerből, melynek uniója lefedi K-t kiválasztható véges sok nyílt halmaz is, melyek véges uniója még mindig lefedi K-t.

Heine-Borel-tétel. Korlátos és zárt halmaz kompakt.

Sorozatkompakt egy K halmaz, ha minden benne haladó sorozatból kiválasztható K-beli határértékű konvergens részsorozat.

Bolzano-Weierstrass-tétel. Korlátos és zárt halmaz sorozatkompakt.

Rn-ben tehát a kompaktság ugyanaz, mint a sorozatkompaktság.

Bolzano-Weierstrass-féle kiválasztási tétel. Korlátos sorozatnak van konvergens részsorozata.

Ha még azt a tényt is hozzávesszük, hogy egy H halmaz pontosan akkor zárt, ha minden benne haladó konvergens sorozatnak a határértéke is benne van, akkor világos, hogy mi a kapcsolat a két utóbbi tétel között.

Rn véges dimenziószáma nagyon lényegesen hozzájárul a fenti tételek fennállásához. Általában (Haussdorf-térben) kompakt halmaz korlátos és zárt. Ám, van olyan végtelen dimenziós normált tér, melyben zárt és korlátos halmaz nem kompakt. Legyen ugyanis 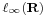\mbox{ }_{\ell_{\infty}(\mathbf{R})} a korlátos sorozatok tere. A téren a norma a suprémum:

||s||_{\infty}=\sup\{|s_n|\mid n\in\mathbf{N}\}

Ekkor a

H:=\{s\in\ell^{\infty}(\mathbf{R})\mid ||s||\leq 1\}

"gömb" nem kompakt. Hasonló furcsaságokat jelentkeznek a p-edik hatványon szummálható sorozatok 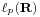\mbox{ }_{\ell_{p}(\mathbf{R})} terében is. Számunkra esetleg a véges sorösszeggel rendelkező 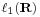\mbox{ }_{\ell_{1}(\mathbf{R})} tér bír jelentőséggel.

Folytonosság

Azt mondjuk, hogy az Rn egy A részhalmazán értelezett és Rm-be ható f leképezés folytonos az értelmezési tartománya egy a ∈ A pontjában

(\forall\varepsilon>0)(\exists\delta>0)(\forall x\in A)(||x-a||<\delta\Longrightarrow||f(x)-f(a)||<\varepsilon)

Itt ||x-a|| az x-a Rn-beli euklideszi normája, ||f(x)-f(a)|| pedig az f(x)-f(a) Rm-beli euklideszi normája.

1. feladat: Igazoljuk, hogy az
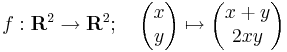
f:\mathbf{R}^2\rightarrow\mathbf{R}^2;\quad\begin{pmatrix}x\\y\end{pmatrix}\mapsto\begin{pmatrix}x+y\\2xy\end{pmatrix}

leképezés folytonos a 0 pontban.

megoldás
A lap eredeti címe: „http://wiki.math.bme.hu/index.php?title=Matematika_A2a_2008/2._gyakorlat&oldid=3189”
Személyes eszközök