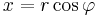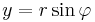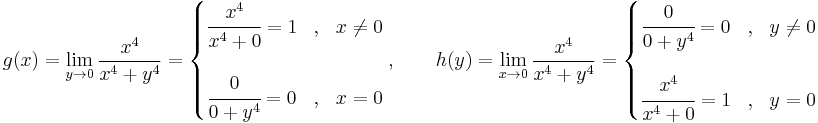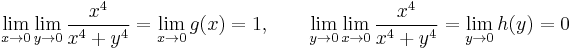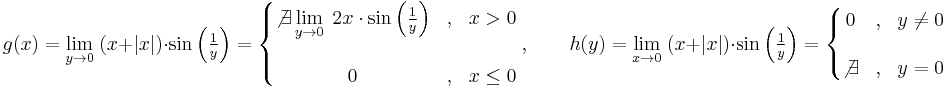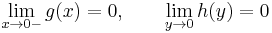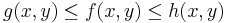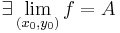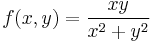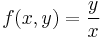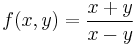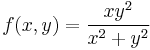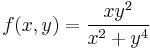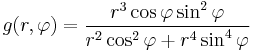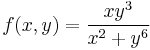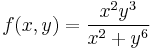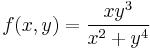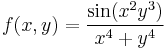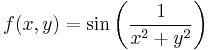Matematika A2a 2008/2. gyakorlat
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Kétváltozós függvények szemléltetése
a) 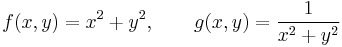
b) 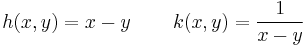
Ezek (x,y,z) koordinátarendszerbeli z=f(x,y) felülettel ábrázolva hengerszimmetrikusak, érdemes az
polárkoordináta transzformációval átírni, ebben 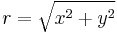 a z-tengelytől mért távolság, és az első és második (majd a második és harmadik síknegyedben):
a z-tengelytől mért távolság, és az első és második (majd a második és harmadik síknegyedben): 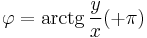
Innen: 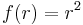 z körül körbeforgatott parabola (forgási paraboloid)
z körül körbeforgatott parabola (forgási paraboloid)
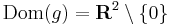 és
és 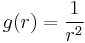 másodfokú hiperbola körbeforgatva.
másodfokú hiperbola körbeforgatva.
Mindkettő szintvonalai körök.
b) h(x,y)=z=x-y egy sík egyenlete, szintvonalai: c=x-y, y=x-c egyenesek.
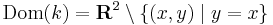 szintén egyenesek a szintvonalak:
szintén egyenesek a szintvonalak: 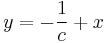 .
.
Iterált határérték
a) 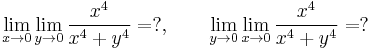
b*) 
c) HF 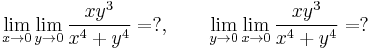
MO.
a)
b)
Tehát g csak a nemnegatívokon értelmezett és ott 0:
*Feladat. a) Ha az iterált határértékek léteznek, de nem egyenlők, akkor a határérték nem létezik. b) Van olyan, hogy az iterált határérték nem létezik, de a határérték igen. c) Van olyan, hogy az iterált határértékek léteznek és egyenlők, de a határérték nem létezik.
Határérték
Def. Tegyük fel, hogy az 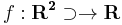 függvény értelmezési tartományának (x0,y0) torlódási pontja. Azt mondjuk, hogy f-nek létezik határértéke az (x0,y0) pontban, és ez az A szám, ha
függvény értelmezési tartományának (x0,y0) torlódási pontja. Azt mondjuk, hogy f-nek létezik határértéke az (x0,y0) pontban, és ez az A szám, ha
- minden ε>0-ra létezik δ>0, hogy
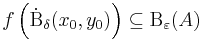
Ilyenkor 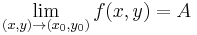 -t vagy
-t vagy 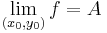 -t írunk.
-t írunk.
Rendőrelv. Legyen 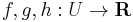 és
és 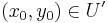 . Ha van olyan δ>0, hogy minden
. Ha van olyan δ>0, hogy minden 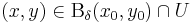 -ra
-ra
és 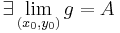 és
és 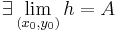 , akkor
, akkor
Határérték nem létezésének jellemzése. Tegyük fel, hogy az 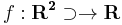 függvény értelmezési tartományának (x0,y0) torlódási pontja. f-nek nem létezik véges határértéke az (x0,y0) pontban, pontosan akkor, ha léteznek olyan
függvény értelmezési tartományának (x0,y0) torlódási pontja. f-nek nem létezik véges határértéke az (x0,y0) pontban, pontosan akkor, ha léteznek olyan 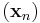 és
és 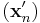 sorozatok, hogy
sorozatok, hogy 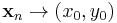 és
és 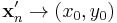 , de
, de 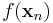 vagy
vagy 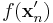 nem konvergensek, vagy ha igen, akkor
nem konvergensek, vagy ha igen, akkor 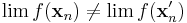 .
.
Folytonosság. Legyen 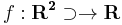 és
és 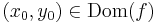 . Azt mondjuk, hogy f folytonos az (x0,y0) pontban, ha
. Azt mondjuk, hogy f folytonos az (x0,y0) pontban, ha
- minden ε>0-ra létezik δ>0, hogy
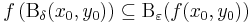
Ha 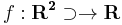 olyan, hogy
olyan, hogy 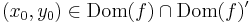 , akkor
, akkor 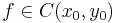 pontosan akkor, ha
pontosan akkor, ha 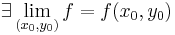 .
.
1. Hol létezik határértéke az
függvénynek? ("A félév függvénye.")
2. Hol létezik határértéke az
függvénynek?
3. Hol létezik határértéke az
függvénynek?
4. Hol létezik határértéke az
függvénynek? (Használjuk az ![|f(x,y)|\leq g(r)\xrightarrow[r\to 0]\, 0](/upload/math/8/3/d/83d45d97d88d983b42cddea534631489.png) , akkor
, akkor ![f(x,y)\xrightarrow[(x,y)\to (0,0)]\,0](/upload/math/e/e/1/ee1b25786ab71d9147e70c5bd1ed4996.png) "rendőrelvet", ahol
"rendőrelvet", ahol 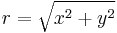 , vagy vegyük észre a "félév függvényét".)
, vagy vegyük észre a "félév függvényét".)
5. Hol létezik határértéke az
függvénynek? (Használjuk az "x2 = x4" trükköt!)
6. Mik az iterált határértékei a (0,0) pontban a
függvénynek?
7. HF. Hol létezik határértéke az
függvénynek?
8. HF. Hol létezik határértéke az
függvénynek?
9. Hol létezik határértéke az
függvénynek? (Vegyük észre a "félév függvényét", vagy írjuk fel a számtani és mértani közép közötti egyenlőtlenséget a nevező tagjaira.)
10. Hol létezik határértéke az
függvénynek? (Használjuk az ![\frac{\sin \vartheta}{\vartheta}\xrightarrow[\vartheta\to 0]\,1](/upload/math/3/3/8/338651eec220434dd235b495979ac806.png) határértéket.)
határértéket.)
11. Hol létezik határértéke az
függvénynek?
| 1. gyakorlat | 3. gyakorlat |