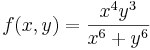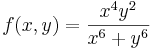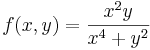Matematika A2a 2008/3. gyakorlat
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) |
||
| 1. sor: | 1. sor: | ||
:''Ez az szócikk a [[Matematika A2a 2008]] alszócikke.'' | :''Ez az szócikk a [[Matematika A2a 2008]] alszócikke.'' | ||
Ezen a konkrét gyakorlaton konkrét függvények konkrét folytonosságát és konkrét határértékét vizsgáljuk meg konkrét módon. | Ezen a konkrét gyakorlaton konkrét függvények konkrét folytonosságát és konkrét határértékét vizsgáljuk meg konkrét módon. | ||
| + | '''Definíció''' Legyen ''D'' ⊆ '''R'''<sup>N</sup>, | ||
| + | f: ''D'' <math>\to</math> '''R'''<sup>M</sup>, ''A'' ∈ '''R'''<sub>M</sub>, ''u'' ∈ '''R'''<sup>N</sup>; torlódási pontja ''D''-nek. Azt mondjuk, hogy az f függvény határértéke az ''u'' pontban az ''A'', ha | ||
| + | ∀ε>0 ∃δ>0 ∀x∈''D'' x ∈ B<sub>δ</sub>(u) <math> \Rightarrow</math> B<sub>ε</sub>(A) | ||
| + | |||
==Határértékfeladatok== | ==Határértékfeladatok== | ||
Van-e folytonos kiterjesztése az alábbi függvényeknek? | Van-e folytonos kiterjesztése az alábbi függvényeknek? | ||
A lap 2009. február 20., 15:48-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Ezen a konkrét gyakorlaton konkrét függvények konkrét folytonosságát és konkrét határértékét vizsgáljuk meg konkrét módon.
Definíció Legyen D ⊆ RN,
f: D  RM, A ∈ RM, u ∈ RN; torlódási pontja D-nek. Azt mondjuk, hogy az f függvény határértéke az u pontban az A, ha
∀ε>0 ∃δ>0 ∀x∈D x ∈ Bδ(u)
RM, A ∈ RM, u ∈ RN; torlódási pontja D-nek. Azt mondjuk, hogy az f függvény határértéke az u pontban az A, ha
∀ε>0 ∃δ>0 ∀x∈D x ∈ Bδ(u) 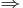 Bε(A)
Bε(A)
Tartalomjegyzék |
Határértékfeladatok
Van-e folytonos kiterjesztése az alábbi függvényeknek?
1.
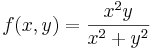
- 1. megoldás (polártranszf.). x = r
 cos(φ), y = r
cos(φ), y = r sin(φ):
sin(φ):
- Ami 0-hoz tartó szor korlátos, amennyiben (x,y)
 (0,0) ( (x,y) tart 0 esetén r tart a 0-hoz, a trigonometrikusak megmindenhogy nézve korlátosak), azaz a határértkék 0.
(0,0) ( (x,y) tart 0 esetén r tart a 0-hoz, a trigonometrikusak megmindenhogy nézve korlátosak), azaz a határértkék 0.
- 2. megoldás (mértani-négyzetes közepek). |x||y|
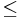 (x2 + y2)/2. Továbbá x2 = |x||x| és y = |y|
(x2 + y2)/2. Továbbá x2 = |x||x| és y = |y| sgn(y), így
sgn(y), így
- Ha (x,y)
 (0,0), akkor persze |x|
(0,0), akkor persze |x|  0 és a többi tényező szorzata korlátos éspedig -1/2 és 1/2 közötti, hiszen a hányados kisebb egyenlő 1. Ezért a határérték 0.
0 és a többi tényező szorzata korlátos éspedig -1/2 és 1/2 közötti, hiszen a hányados kisebb egyenlő 1. Ezért a határérték 0.
- 1. megoldás (polártranszf.). x = r
2.
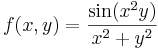
- Megoldás.
- Innen pedig a sin(α)/α és az előző határérték miatt tart a 0-hoz.
- Megoldás.
3.
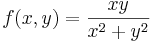
- Megoldás. Világos, hogy a polárkoordináta transzformációval az r kiesik és csak φ-től függ. Ezért érdemes a (0,0) pontot több irnyból, sugárirányba megközelíteni, általánosan az y = mx egyenes mentén:
- Vagyis m=0-ra ez 0-t, m=1-re ez 1/2-et ad. Eszerint nincs a (0,0)-ban határérték, mert van két különböző határértékű függvényértéksorozat, miközben a sorozatokkal a (0,0)-ba tartunk.
- Megoldás. Világos, hogy a polárkoordináta transzformációval az r kiesik és csak φ-től függ. Ezért érdemes a (0,0) pontot több irnyból, sugárirányba megközelíteni, általánosan az y = mx egyenes mentén:
4.
5.
6.
7.
8.
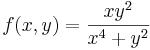
- (Először az x szorzó nélküli tényező korlátosságát igazoljuk!)
9.
| 2. gyakorlat | pótló gyakorlat |
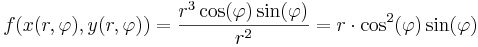
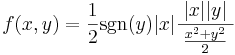
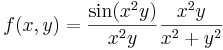
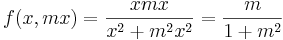
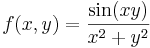
![f(x,y)=\frac{x^2y}{\sqrt[5]{x^2+y^2}}](/upload/math/3/8/6/38613f6a1f08dc2512f6baea3466a691.png)