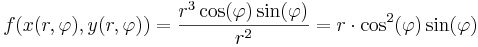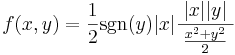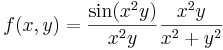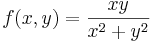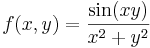Matematika A2a 2008/3. gyakorlat
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→1.) |
Mozo (vitalap | szerkesztései) (→2.) |
||
| 14. sor: | 14. sor: | ||
===2.=== | ===2.=== | ||
:<math>f(x,y)=\frac{\sin(x^2y)}{x^2+y^2}</math> | :<math>f(x,y)=\frac{\sin(x^2y)}{x^2+y^2}</math> | ||
| + | ::'''Megoldás.''' | ||
| + | :::<math>f(x,y)=\frac{\sin(x^2y)}{x^2y}\frac{x^2y}{x^2+y^2}</math> | ||
| + | ::Innen pedig a sin(φ)/φ és az előző határérték miatt tart a 0-hoz. | ||
| + | |||
===3.=== | ===3.=== | ||
:<math>f(x,y)=\frac{xy}{x^2+y^2}</math> | :<math>f(x,y)=\frac{xy}{x^2+y^2}</math> | ||
===2.=== | ===2.=== | ||
:<math>f(x,y)=\frac{\sin(xy)}{x^2+y^2}</math> | :<math>f(x,y)=\frac{\sin(xy)}{x^2+y^2}</math> | ||
A lap 2008. február 22., 23:42-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Ezen a gyakorlaton konkrét függvények folytonosságát és határértékét vizsgáljuk meg.
Tartalomjegyzék |
Határértékfeladatok
Van-e folytonos kiterjesztése az alábbi függvényeknek?
1.
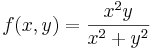
- 1. megoldás (polártranszf.). x = r
cos(φ), y = rsin(φ):
- Ami 0-hoz tartó szor korlátos, amennyiben (x,y)
(0,0), azaz a határértkék 0.
- 2. megoldás (mértani-négyzetes közepek). |x||y|
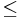(x2 + y2)/2. Továbbá x2 = |x||x| és y = |y|sgn(y), így
- Ha (x,y) (0,0), akkor persze |x| 0 és a többi tényező szorzata korlátos éspedig -1/2 és 1/2 közötti, hiszen a hányados kisebb egyenlő 1. Ezért a határérték 0.
- 1. megoldás (polártranszf.). x = r
2.
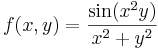
- Megoldás.
- Innen pedig a sin(φ)/φ és az előző határérték miatt tart a 0-hoz.
- Megoldás.
