Matematika A2a 2008/4. gyakorlat
Mozo (vitalap | szerkesztései) (→Lineáris leképezések) |
Mozo (vitalap | szerkesztései) |
||
| 1. sor: | 1. sor: | ||
:''Ez az szócikk a [[Matematika A2a 2008]] alszócikke.'' | :''Ez az szócikk a [[Matematika A2a 2008]] alszócikke.'' | ||
| + | ==Parciális deriváltak== | ||
| + | |||
| + | '''Definíció.''' Legyen ''f'': '''R'''<sup>n</sup> <math>\supset\!\to</math> '''R''', ''u'' ∈ int Dom(''f''). Azt mondjuk, hogy f parciálisan differenciálható az ''u'' pontban a ''x''<sub>i</sub> változó szerint, ha az | ||
| + | :<math>f(u_1,...,.,...,u_n): x_i\mapsto f(u_1,...x_i,...,u_n)\,</math> | ||
| + | egyváltozós valós függvény differenciálható az u<sub>i</sub> pontban. Ekkor a fenti függvény <math>u_i</math>-beli deriváltját | ||
| + | :<math>\partial_if(u),\quad f'_{x_i}(u),\quad f_{x_i}(u),\quad\left.\frac{\partial f}{\partial x_i}\right|_{x=u}</math> | ||
| + | jelöli. | ||
| + | |||
| + | Példa: | ||
| + | :<math>\frac{\partial x^2\cdot\sin(y)}{\partial x}=2x\cdot \sin(y)</math> | ||
| + | :<math>\frac{\partial x^2\cdot\sin(y)}{\partial y}=x^2\cdot \cos(y)</math> | ||
| + | :<math>\frac{\partial x^2\cdot\sin(y)}{\partial z}=0</math> | ||
| + | |||
| + | :<math>\frac{\partial \sin(\mathrm{sh}(x)y^2)}{\partial x}=\cos(\mathrm{sh}(x)y^2)\cdot \mathrm{ch}(x)y^2</math> | ||
| + | |||
| + | '''Feladat.''' Parciálisan deriválható-e az | ||
| + | :<math>f(x,y)=\sqrt{x^2+y^2}</math> | ||
| + | a (0,0)-ban? | ||
| + | |||
| + | '''Feladat.''' Parciálisan deriválható-e az | ||
| + | :<math>f(x,y)=\left\{\begin{matrix} | ||
| + | 0,& \mbox{ ha }(x,y)=(0,0)\\ | ||
| + | (x^2+y)\sin\frac{1}{|x|+|y|},& \mbox{ ha }(x,y)\ne(0,0) | ||
| + | \end{matrix}\right.</math> | ||
| + | a (0,0)-ban? | ||
| + | |||
==Lineáris leképezések== | ==Lineáris leképezések== | ||
A lap 2013. szeptember 29., 10:14-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Tartalomjegyzék |
Parciális deriváltak
Definíció. Legyen f: Rn 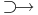 R, u ∈ int Dom(f). Azt mondjuk, hogy f parciálisan differenciálható az u pontban a xi változó szerint, ha az
R, u ∈ int Dom(f). Azt mondjuk, hogy f parciálisan differenciálható az u pontban a xi változó szerint, ha az
egyváltozós valós függvény differenciálható az ui pontban. Ekkor a fenti függvény ui-beli deriváltját
jelöli.
Példa:
Feladat. Parciálisan deriválható-e az
a (0,0)-ban?
Feladat. Parciálisan deriválható-e az
a (0,0)-ban?
Lineáris leképezések
A V1 és V2 vektorterek között ható A leképezést akkor nevezünk lineárisnak, ha teljesül minden λ, μ ∈ R és v, u ∈ V1
A definícióból rögtön következik, hogy a nulla vektor képe nulla:
viszont más elem a V2 nem feltétlenül vétetik föl.
Véges dimenziós terek közti lineáris leképezés a bázis választásával egyértelműen jellemezhető az alábbi mátrixszal.
ahol B = (b1,b2,…,bn) a V1 egy bázisa, C az V2 bázisa, a mátrix oszlopai pedig a B elemeinek 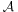 általi képvektoraiból, mint oszlopvektorokból áll. Ha
általi képvektoraiból, mint oszlopvektorokból áll. Ha 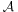 V
V  V típusú, akkor csak
V típusú, akkor csak ![\mbox{ }_{[\mathcal{A}]_B}](/upload/math/1/5/6/156d0043945fe751a951df3818cbfb93.png) -t szokás írni, ha pedig pusztán
-t szokás írni, ha pedig pusztán ![\mbox{ }_{[\mathcal{A}]}](/upload/math/a/b/0/ab06c27145a3fa90b92cfb08c9e0d4fe.png) -t írnak, akkor az azt jelenti, hogy a Rn sztenderd bázisáról van szó, azaz a
-t írnak, akkor az azt jelenti, hogy a Rn sztenderd bázisáról van szó, azaz a
vektorrendszerről.
Példák
1. Forgatás az origo körül φ szöggel:
Világos, hogy ez invertálható leképezés és az inverze a -φ szögű forgatás.
2. Tükrözés a φ szőgű egyenesre.
Világos, hogy ez is invertálható és inverze saját maga.
Ezek ortogonális transzformációk, azaz a transzponáltjuk az inverzük. Speciálisan a tükrözés szimmetrikus leképezés, mert mátrixa szimmetrikus. Sőt, ezek alkotják a síkon az összes ortogonális transzformációt.
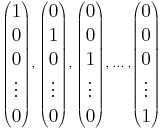
3. Deriváló operáció. Legyen V a legfeljebb másodfokú polinomfüggvények tere. Ekkor a
lineáris leképezés:
Bázis V-ben: {1, x, x2}, ezért a mátrixa:
Világos, hogy a leképezés képzere nem a teljes V, hanem annak egy altere (a legfeljebb elsőfokú polinomfüggvények tere) és nem csak a 0 polinom képe 0, hanem minden konstans polinomé.
Lineáris leképezések folytonossága
Megjegyzés. A normált terek között ható A lineáris leképezés folytonos, ha a 0-ban folytonos.
Ugyanis, legyen az A: N1  N2 lineáris leképezés és tegyük fel, hogy 0-ban folytonos, azaz minden ε>0-ra létezik δ>0, hogy minden x ∈ Bδ(0)-ra Ax ∈ Bε(0).
N2 lineáris leképezés és tegyük fel, hogy 0-ban folytonos, azaz minden ε>0-ra létezik δ>0, hogy minden x ∈ Bδ(0)-ra Ax ∈ Bε(0).
Most ha ε > 0 tetszőleges és x1 és x2 N1-beliek is tetszőlegesek, akkor
amennyiben x1-x2 ∈ Bδ(0), ahol δ a 0-beli folytonosság által az ε-hoz tartozó δ.
Tétel. A : Rn  Rm lineáris leképzés folytonos, sőt:
Rm lineáris leképzés folytonos, sőt:
Megjegyzés. Ez azt is jelenti, hogy egy ilyen leképezés Lipschitz-függvény. Az f: Rn ⊃ Rm függvényt Lipschitz-függvénynek nevezük, ha létezik L nemnegatív szám, hogy minden x1 és x2 Dom(f)-belire:
Rm függvényt Lipschitz-függvénynek nevezük, ha létezik L nemnegatív szám, hogy minden x1 és x2 Dom(f)-belire:
Világos, hogy ez lineáris leképezésre ekvivalens a tételbeli megfogalmazással.
Ha lipschitzes, akkor pedig folytonos, mert ekkor δ=ε/(L+1)-gyel
Bizonyítás. Vegyük az A sztenderd bázis beli mátrixát. Ekkor A(x)=A x. Így A minden Ai sorára
x. Így A minden Ai sorára
ahol Li rögzített i mellett a {|Ai,j|} j=1...n számok maximuma. Ha most vesszük L = max {Li}-t is, akkor
is teljesül, azaz a kép maximumnormája felülbecsülhető L-szer a vektor norma-1 szerinti normájával. A normák ekvivalenciája miat pedig alkalmas L-re minden normára igaz.
Operátornorma
A lineáris leképezések Lin(Rn,Rm) tere normált tér, ugyanis vegyük a következő számot:
Ez létezik, mivel x  ||Ax|| folytonos a kompakt 0 középpontú, egységsugarú gömbfelületen.
||Ax|| folytonos a kompakt 0 középpontú, egységsugarú gömbfelületen.
Differenciálhatóság
A többváltozós differenciálhatóságot az egyváltozós alábbi átfogalmazásából általánosítjuk:
Definíció. Legyen f: Rn  Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn
Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn  Rm lineáris leképezés, hogy
Rm lineáris leképezés, hogy
Ekkor A egyértelmű és az f leképezés u-bent beli differenciáljának nevezzük és df(u)-val vagy Df(u)-val jelöljük. Ezt a fogalmat néha teljes differenciálnak, totális differenciálnak vagy Fréchet-deriváltnak is mondjuk.
Megjegyzés. A fenti határérték 0 volta egyenértékű a következő kijelentéssel. Létezik A: Rn  Rm lineáris leképezés és ε: Dom(f)
Rm lineáris leképezés és ε: Dom(f)  Rm függvény, melyre:
Rm függvény, melyre:
- ε folytonos u-ban és ε(u)=0, továbbá
minden x ∈ Dom(f)-re:
Megjegyzés. Azt, hogy A egyértelmű, a következőkkel bizonyíthatjuk. Legyen A és B is a mondott tulajdonságú, azaz létezzenek ε és η az u-ban eltűnő és ott folytonos Dom(f)-en értelmezett függvények, melyekre teljesül, hogy minden x ∈ Dom(f)-re
ezeket kivonva egymásból és használva minden x-re:
így minden x = u + ty értékre is az azonosan nullát kapjuk, ha t pozitív szám, y pedig rögzített nemnulla vektor, azaz minden t-re
az azonosan 0 függény határértéke t 0 esetén szintén nulla:
0 esetén szintén nulla:
hiszen t-t kiemelhetünk és egyszerűsíthetünk és t 0 esetén
ε és η nullává válik.
Ez viszont pont azt jelenti, hogy a két lineéris operátor azonosan egyenlő.
0 esetén
ε és η nullává válik.
Ez viszont pont azt jelenti, hogy a két lineéris operátor azonosan egyenlő.
Jacobi-mátrix
A df(u) lineáris leképezés (e1,e2,...,en) szetenderd bázisbeli mátrixa legyen: [df(u)] = A. Vizsgáljuk mibe viszi a bázisokat df(u) leképezés!
Írjuk fel a definíciót, de az e1 egységvektor mentén tartsunk u-hoz: x = u + te1. Ekkor
ami azért hasznos, mert a
alakból kiemelhetó t:
azaz
vagyis f koordinátafüggvényeinek az első változó szerinti parciális deriváltja az u pontban. A többi oszlopvektor ugyanígy:
amelyet Jacobi-mátrixnak nevezünk.
Következmény. Tehát. ha f totálisan differenciálható, akkor parciálisan is differenciálható és a differenciál sztenderd bázisbeli mátrixa a Jacobi-mátrix.
Azaz:
- teljes differenciálhatóság
 parciális differenciálhatóság
parciális differenciálhatóság
de ez fordítva már nem igaz:
- parciális differenciálhatóság
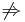 teljes differenciálhatóság
teljes differenciálhatóság
Erre vonatkozik a két alábbi példa.
| pótló gyakorlat | 5. gyakorlat |
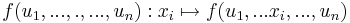
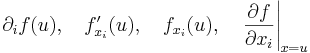
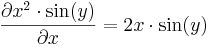
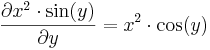
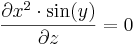
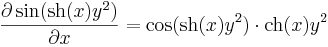
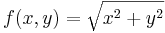
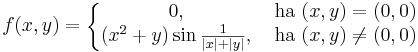

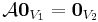
![[\mathcal{A}]_{B,C} = \begin{bmatrix}
\begin{matrix}\vert \\ \vert \\ \mathcal{A}\mathbf{b}_1 \\ \vert \\ \vert \end{matrix}& \begin{matrix}\vert \\ \vert \\ \mathcal{A}\mathbf{b}_2 \\ \vert \\ \vert \end{matrix} & ... & \begin{matrix}\vert \\ \vert \\ \mathcal{A}\mathbf{b}_n \\ \vert \\ \vert \end{matrix}
\end{bmatrix}](/upload/math/e/2/1/e218d5327c820937af47e217f5212ec7.png)
![[\mathcal{F}_\varphi]=\begin{bmatrix}\cos\varphi & -\sin\varphi \\ \sin\varphi & \cos\varphi \end{bmatrix}](/upload/math/1/b/d/1bd899a86970ed93aad1b307d1af4e0b.png)
![[\mathcal{T}_\varphi]=\begin{bmatrix}\cos(2\varphi) & \sin(2\varphi) \\ \sin(2\varphi) & -\cos(2\varphi) \end{bmatrix}](/upload/math/4/f/3/4f3d3c1c23cacad098bf0349140e0d0f.png)
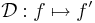
![[\mathcal{D}]=
\begin{bmatrix}
0 & 1 & 0 \\
0 & 0 & 2\\
0 & 0 & 0
\end{bmatrix}](/upload/math/a/7/a/a7ad5c2aa1f95e6c92807ec3550700c1.png)
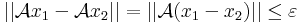
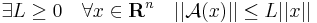
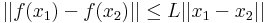
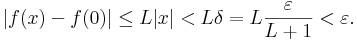
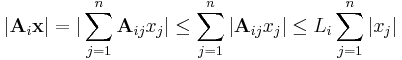
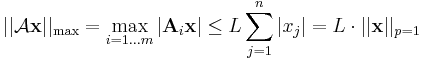
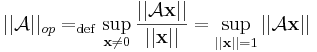
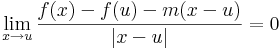

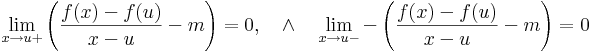
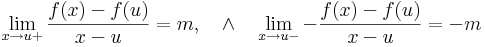
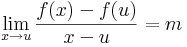
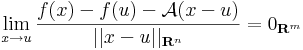
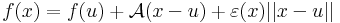
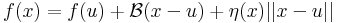
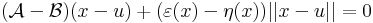
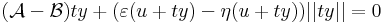
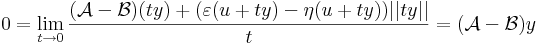
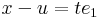
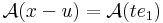
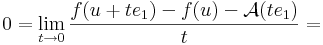
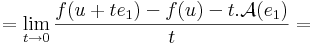
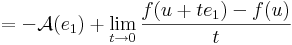
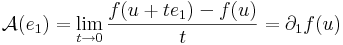
![[\mathrm{d}f(u)]=\mathbf{J}^f(u)=\begin{bmatrix}
\partial_1 f_1(u) & \partial_2 f_1(u) & \dots & \partial_n f_1(u)\\
\partial_1 f_2(u) & \partial_2 f_2(u) & \dots & \partial_n f_2(u)\\
\vdots & \vdots & \ddots & \vdots \\
\partial_1 f_m(u) & \partial_2 f_m(u) & \dots & \partial_n f_m(u)\\
\end{bmatrix}](/upload/math/b/c/8/bc8c1cf3c3d6f5032a7858552cc82a3a.png)