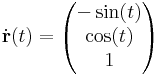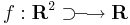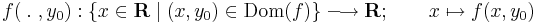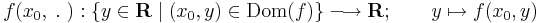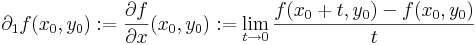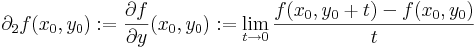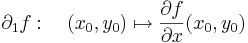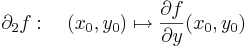Matematika A2a 2008/4. gyakorlat
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Deriváltfogalmak Rn-ben
A többdimenziós terekben több természetes általánosítására lelhetünk az egyváltozós függvények deriváltfogalmának. A következőkben konkrét esetekt nézünk.
Görbék
A görbék lényegében egyváltozós vektorértékű függvények: r: I R3; t
R3; t  r(t). Ezekre a deriváltat definiáló határérték válzatlan alakban írható:
r(t). Ezekre a deriváltat definiáló határérték válzatlan alakban írható:
feltéve, hogy ez a határérték egyáltalán létezik az R3 normájában. A geometriai jelentésből az is következik, hogy a fenti határérték ugyanúgy a szelők határértékét, azaz az érintőt adják, mint az egyváltozós függvények esetén. Ekkor t jelentése: idő. A komponensenkénti határértékképzés miatt világos, hogy
Ezt még a görbe idő szerinti paraméterezésének is nevezzük, melynek fenti deriváltja a sebességet adja és vessző helyett ponttal is jelöljük a deriváltat:
Példa.
egy spirál paraméterezése. A deriváltja:
amiből látszik, hogy az [xy] síkra vett vetülete egy egyenletes körmozgás, a z tengelyre eső vetülete pedig egy egyenesvonalú egyenletes mozgás.
Felületek
Ha adott az
kétváltozós függvény, akkor adott (x0,y0) ∈ Dom(f) pont körül ebből származtathatunk két egyváltozós függvényt:
Ezeket parciális függvényeknek nevezzük, és ha differenciálhatóak rendre az x0 és az y0 pontokban, akkor a deriváltjuk a parciális deriváltak:
Geometriailag ezek a (x0,y0) pontban állított [x,z] síkkal illetve az [yz] síkkal vett metszetgörbék, mint egyváltozós függvények deriváltjai. A parciális deriváltfüggvényeket már mint kétváltozós függvényekként definiáljuk:
Példa.
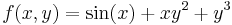 , akkor
, akkor 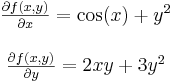
| pótló gyakorlat | 5. gyakorlat |
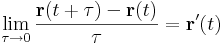
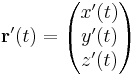
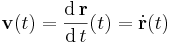
![\mathbf{r}:[0,4\pi]\longrightarrow\mathbf{R}^3;\quad \mathbf{r}(t)=\begin{pmatrix}\cos(t)\\\sin(t)\\t\end{pmatrix}](/upload/math/1/1/4/114aa7c0e95ad98aaef1d6f051ffcc2b.png)