|
|
| (egy szerkesztő 24 közbeeső változata nincs mutatva) |
| 1. sor: |
1. sor: |
| − | :''Ez az szócikk a [[Matematika A2a 2008]] alszócikke.''
| + | ==Differenciálhatóság== |
| − | ==Másodrendű parciális deriváltak== | + | A többváltozós differenciálhatóságot az egyváltozós alábbi átfogalmazásából általánosítjuk: |
| − | Ha ''f'' a ''H'' ⊆ '''R'''<sup>2</sup> halmazon értelmezett '''R'''-be képező, az ''u'' ∈ ''H''-ban differenciálható függvény és a
| + | |
| − | :<math>\mathrm{grad}\,f</math> | + | |
| − | gradiensfüggvény szintén differenciálható ''u''-ban, akkor ''f''-et ''u''-ban kétszer differenciálhatónak nevezzük és az ''f'' függény ''u''-beli '''másodrendű differenciálja''':
| + | |
| − | :<math>\mathrm{d}^2f(u):=\mathrm{d}(\mathrm{grad}\,f)(u)</math>
| + | |
| − | Ennek Jacobi-mátrixa akkor is létezik, ha csak azt feltételezzük, hogy a parciális deriváltak léteznek az ''u'' egykörnyezetében, és ott differenciálhatóak. Ekkor a szóban forgó Jacobi-mátrix kvadratikus és
| + | |
| − | :<math>H^f(u)=\begin{bmatrix}
| + | |
| − | \cfrac{\partial^2 f(u)}{\partial x^2} & \cfrac{\partial^2 f(u)}{\partial y\partial x}\\\\
| + | |
| − | \cfrac{\partial^2 f(u)}{\partial x\partial y} & \cfrac{\partial^2 f(u)}{\partial y^2}
| + | |
| − | \end{bmatrix}</math>
| + | |
| − | alakú, amit '''Hesse-féle mátrix'''nak nevezünk.
| + | |
| | | | |
| − | A vegyes másodrendű parciális deriváltakra vonatkozik a Young-tétel:
| + | :<math>\lim\limits_{x\to u}\frac{f(x)-f(u)-m(x-u)}{|x-u|}=0</math> |
| | + | :<math>\lim\limits_{x\to u+}\frac{f(x)-f(u)-m(x-u)}{x-u}=0\quad\wedge\quad\lim\limits_{x\to u-}\frac{f(x)-f(u)-m(x-u)}{-(x-u)}=0</math> |
| | + | :<math>\lim\limits_{x\to u+}\left(\frac{f(x)-f(u)}{x-u}-m\right)=0,\quad\wedge\quad\lim\limits_{x\to u-}-\left(\frac{f(x)-f(u)}{x-u}-m\right)=0</math> |
| | + | :<math>\lim\limits_{x\to u+}\frac{f(x)-f(u)}{x-u}=m,\quad\wedge\quad\lim\limits_{x\to u-}-\frac{f(x)-f(u)}{x-u}=-m</math> |
| | + | :<math>\lim\limits_{x\to u}\frac{f(x)-f(u)}{x-u}=m</math> |
| | | | |
| − | '''Tétel''' (''Young'') Kétszer differenciálható függvény vegyes másodrendű parciális deriváltjai egyenlők.
| |
| | | | |
| − | (A tétel egy gyenge verziójának könnyen átlátható szemléletes bizonyítása megtalálható itt: [[User:Mozo/egyéb#Young-tétel]].) | + | '''Definíció.''' Legyen ''f'': '''R'''<sup>n</sup> <math>\supset\!\longrightarrow</math> '''R'''<sup>m</sup> és ''u'' ∈ int Dom(f). Azt mondjuk, hogy ''f'' '''differenciálható''' az ''u'' pontban, ha létezik olyan ''A'': '''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképezés, hogy |
| | + | :<math>\lim\limits_{x\to u}\frac{f(x)-f(u)-\mathcal{A}(x-u)}{||x-u||_{\mathbf{R}^n}}=0_{\mathbf{R}^m}</math> |
| | + | Ekkor ''A'' egyértelmű és az ''f'' leképezés ''u''-bent beli '''differenciál'''jának nevezzük és d''f''(''u'')-val vagy D''f''(u)-val jelöljük. Ezt a fogalmat néha ''teljes differenciál''nak, ''totális differenciál''nak vagy ''Fréchet-derivált''nak is mondjuk. |
| | | | |
| − | A Young-tétel értelmében a Hesse-mátrix szimmetrikus illetve a d<sup>2</sup>''f''(u) szimmetrikus tenzor | + | '''Megjegyzés.''' A fenti határérték 0 volta egyenértékű a következő kijelentéssel. Létezik ''A''': ''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképezés és ε: Dom(''f'') <math>\to</math> '''R'''<sup>m</sup> függvény, melyre: |
| − | :<math>H^f(u)=(H^f(u))^{\mathrm{T}}=\begin{bmatrix} | + | : ε folytonos u-ban és ε(u)=0, továbbá |
| − | \partial_{11} f(u) & \partial_{12} f(u)\\\\ | + | minden ''x'' ∈ Dom(''f'')-re: |
| − | \partial_{12} f(u) & \partial_{22} f(u)\\ | + | : <math>f(x)=f(u)+\mathcal{A}(x-u)+\varepsilon(x)||x-u||</math> |
| − | \end{bmatrix}</math> | + | '''Megjegyzés.''' Azt, hogy ''A'' egyértelmű, a következőkkel bizonyíthatjuk. Legyen ''A'' és ''B'' is a mondott tulajdonságú, azaz létezzenek ε és η az ''u''-ban eltűnő és ott folytonos Dom(''f'')-en értelmezett függvények, melyekre teljesül, hogy minden ''x'' ∈ Dom(''f'')-re |
| | + | :<math>f(x)=f(u)+\mathcal{A}(x-u)+\varepsilon(x)||x-u||</math> |
| | + | :<math>f(x)=f(u)+\mathcal{B}(x-u)+\eta(x)||x-u||</math> |
| | + | ezeket kivonva egymásból és használva '''minden''' ''x''-re: |
| | + | :<math>(\mathcal{A}-\mathcal{B})(x-u)+(\varepsilon(x)-\eta(x))||x-u||=0</math> |
| | + | így minden x = u + ty értékre is az azonosan nullát kapjuk, ha t pozitív szám, y pedig rögzített nemnulla vektor, azaz minden t-re |
| | + | :<math>(\mathcal{A}-\mathcal{B})ty+(\varepsilon(u+ty)-\eta(u+ty))||ty||=0</math> |
| | + | az azonosan 0 függény határértéke t<math>\to</math> 0 esetén szintén nulla: |
| | + | :<math> 0=\lim\limits_{t\to 0}\frac{(\mathcal{A}-\mathcal{B})(ty)+(\varepsilon(u+ty)-\eta(u+ty))||ty||}{t}=(\mathcal{A}-\mathcal{B})y</math> |
| | + | hiszen t-t kiemelhetünk és egyszerűsíthetünk és t<math>\to</math> 0 esetén |
| | + | ε és η nullává válik. |
| | + | Ez viszont pont azt jelenti, hogy a két lineéris operátor azonosan egyenlő. |
| | | | |
| − | Általában a deriváltmátrixok nem szimmetrikusak, ez egy különleges tulajdonsága a második differenciálnak. Sőt, általában az a kérdés, hogy mi a deriválttenzor szimmetrikus és antiszimmetrikus része.
| + | ==Jacobi-mátrix== |
| | + | A d''f''(''u'') lineáris leképezés (<math>e_1</math>,<math>e_2</math>,...,<math>e_n</math>) szetenderd bázisbeli mátrixa legyen: [d''f''(''u'')] = '''A'''. Vizsgáljuk mibe viszi a bázisokat d''f''(''u'') leképezés! |
| | | | |
| − | '''Megjegyzés.''' Elvileg a
| + | Írjuk fel a definíciót, de az <math>e_1</math> egységvektor mentén tartsunk ''u''-hoz: ''x'' = ''u'' + ''t''<math>e_1</math>. Ekkor |
| − | :<math>\{x\in \mathbf{R}^2\mid f\in\mathrm{Diff}(x)\}\rightarrow\mathrm{Lin}(\mathbf{R}^2;\mathbf{R});\quad x\mapsto \mathrm{d}f(x)</math>
| + | :<math>x-u=te_1\,</math> |
| − | leképezésnek kellett volna a differenciálját venni az ''u'' pontban, és ezt tekinteni a differenciálnak. Ám ez nem '''R'''<sup>m</sup>-be, hanem egy általánosabb normált térbe, a '''R'''<sup>2</sup> <math>\to</math> '''R''' lináris leképezések terébe képez (az ún. kétváltozós lineáris funkcionálok terébe). Ebben a norma az operátornorma (az operátor minimális Lipschitz-konstansa), és a tér véges dimenziós. A differenciálhatóság pontosan ugyanúgy értelmezhető, mint a többváltozs esetben. Ekkor az ''f'' függvény ''u''-beli másodrendű differenciálja az
| + | ami azért hasznos, mert a |
| − | :<math>\mathrm{d}(\mathrm{d}f(.))(u)=\mathcal{A}:\mathbf{R}^2\rightarrow\mathrm{Lin(\mathbf{R}^2;\mathbf{R})} </math> | + | :<math>\mathcal{A}(x-u)=\mathcal{A}(te_1)\,</math> |
| − | lineáris leképezés, melyre teljesül a
| + | alakból kiemelhetó t: |
| − | :<math>\lim\limits_{x\to u}\frac{\mathrm{d}f(x)-\mathrm{d}f(u)-\mathcal{A}(x-u)}{||x-u||}=0_{\mathrm{Lin(\mathbf{R}^2;\mathbf{R})}}</math> | + | :<math>0=\lim\limits_{t\to 0}\frac{f(u+te_1)-f(u)-\mathcal{A}(te_1)}{t}=</math> |
| − | A bázisvektorokon ''A'' a következőt veszi fel:
| + | :::<math>=\lim\limits_{t\to 0}\frac{f(u+te_1)-f(u)-t.\mathcal{A}(e_1)}{t}=</math> |
| − | :<math>\lim\limits_{t\to 0}\frac{\mathrm{d}f(u+te_1)-\mathrm{d}f(u)}{t}=\mathcal{A}(e_1)</math> | + | :::<math>=-\mathcal{A}(e_1)+\lim\limits_{t\to 0}\frac{f(u+te_1)-f(u)}{t}</math> |
| − | ennek a mátrixa a sztenderd bázisban
| + | azaz |
| − | :<math>\lim\limits_{t\to 0}\frac{[\partial_1 f(u+te_1)\quad\partial_2 f(u+te_1)]-[\partial_1 f(u)\quad\partial_2 f(u)]}{t}=[\mathcal{A}(e_1)]</math> | + | :<math>\mathcal{A}(e_1)=\lim\limits_{t\to 0}\frac{f(u+te_1)-f(u)}{t}=\partial_1 f(u)</math> |
| − | ami a kivonás és az osztást komponensenként elvégezve az parciális deriváltak első változó szerinti parciális deriváltjait adja:
| + | vagyis ''f'' koordinátafüggvényeinek az első változó szerinti parciális deriváltja az ''u'' pontban. A többi oszlopvektor ugyanígy: |
| − | :<math>[\mathcal{A}(e_1)]=[\partial_1(\partial_1 f)(u)\quad \partial_1(\partial_2 f)(u)]=[\partial_{11} f(u)\quad \partial_{12}f(u)]</math> | + | |
| − | Az 1 bázisvektoron felvett érték tehát az a lineáris operártor, melyet a fenti sorvektorral való szorzás határoz meg. A másik bázisvektoron szintén felríható ez a mátrix, így világos, hogy d(df(.))(u) jellemezhető a d<sup>2</sup>f(u) mátrixával, így azonosítható vele.
| + | |
| | | | |
| − | ==A differenciálás tulajdonságai==
| + | :<math>[\mathrm{d}f(u)]=\mathbf{J}^f(u)=\begin{bmatrix} |
| − | ===Lineáris és affin függvény deriváltja===
| + | \partial_1 f_1(u) & \partial_2 f_1(u) & \dots & \partial_n f_1(u)\\ |
| − | Az ''A'' : '''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképezés differenciálható és differenciálja minden pontban saját maga.
| + | \partial_1 f_2(u) & \partial_2 f_2(u) & \dots & \partial_n f_2(u)\\ |
| | + | \vdots & \vdots & \ddots & \vdots \\ |
| | + | \partial_1 f_m(u) & \partial_2 f_m(u) & \dots & \partial_n f_m(u)\\ |
| | + | \end{bmatrix}</math> |
| | + | amelyet '''Jacobi-mátrix'''nak nevezünk. |
| | | | |
| − | ''Ugyanis, '' legyen ''u'' ∈ '''R'''<sup>n</sup>. Ekkor | + | '''Következmény.''' Tehát. ha f totálisan differenciálható, akkor parciálisan is differenciálható és a differenciál sztenderd bázisbeli mátrixa a Jacobi-mátrix. |
| | | | |
| − | :<math>\lim\limits_{x\to u}\frac{\mathcal{A}(x)-\mathcal{A}(u)-\mathcal{A}(x-u)}{||x-u||}=\lim\limits_{x\to u}0=0</math> | + | Azaz: |
| | + | :'''teljes''' differenciálhatóság <math>\Longrightarrow</math> '''parciális''' differenciálhatóság |
| | + | de ez fordítva már nem igaz: |
| | + | : '''parciális''' differenciálhatóság <math>\not\Rightarrow</math> '''teljes''' differenciálhatóság |
| | + | Erre vonatkozik a két alábbi példa. |
| | | | |
| − | c konstans függény esetén az d''c''(''u'') <math>\equiv</math> 0 alkalmas differenciálnak, mert
| |
| − | :<math>\lim\limits_{x\to u}\frac{c-c-0\cdot(x-u)}{||x-u||}=\lim\limits_{x\to u}0=0</math>
| |
| − | így világos, hogy c + ''A'' alakú affin függvények is differenciálhatóak, és differenciáljuk minden pontban az az ''A'' lineáris leképezés, melynek eltolásából az affin származik. Ezt szintén behelyettesítéssel ellenőrizhetjük.
| |
| | | | |
| − | Tehát minden ''u'' ∈ '''R'''<sup>n</sup>-re
| |
| − | :<math>\mathrm{d}\mathcal{A}(u)=\mathcal{A},\quad\quad\mathrm{d}c(u)\equiv 0,\quad\quad\mathrm{d}(b+\mathcal{A}\circ(id-a))(u)=\mathcal{A}</math>
| |
| | | | |
| − | ====Példa====
| |
| − |
| |
| − | Az ''A'': '''x''' <math>\mapsto</math> 2<math>x_1</math> + 3<math>x_2</math> - 4<math>x_3</math> lineáris leképezés differenciálja az '''u''' pontban az '''u'''-tól független
| |
| − | :<math>(\mathrm{d}\mathcal{A}(\mathbf{u}))(x_1,x_2,x_3)=2x_1+3x_2-4x_3\,</math>
| |
| − | és Jacobi-mátrixa a konstans
| |
| − | :<math>\mathbf{J}^\mathcal{A}(\mathbf{u})=\begin{bmatrix}2 & 3 & -4\end{bmatrix}</math>
| |
| − | mátrix.
| |
| − |
| |
| − | Világos, hogy a
| |
| − | :<math>\mathrm{pr}_i:(x_1,x_2,...,x_i,...,x_n)\mapsto x_i</math>
| |
| − | koordináta vagy projekciófüggvény lineáris, differenciálja minden '''u''' pontban saját maga és ennek mátrixa:
| |
| − | :<math>[\mathrm{grad}\,\mathrm{pr_i}]=\mathbf{J}^{\mathrm{pr}_i}(\mathbf{u})=\begin{bmatrix}0 & 0 & ... & 1 & ...& 0\end{bmatrix}</math>
| |
| − | ahol az 1 az i-edik helyen áll. Másként
| |
| − | :<math>\partial_kx_i=\delta_{ki}</math>
| |
| − | ahol
| |
| − | :<math>\delta_{ij}=\left\{\begin{matrix}1, \mbox{ ha }i=j\\0, \mbox{ ha }i\ne j \end{matrix}\right.</math>
| |
| − | azaz a Kronecker-féle δ szimbólum.
| |
| − |
| |
| − | ===Függvények lineáris kombinációja===
| |
| − | Ha ''f'' és ''g'' a ''H'' ⊆ '''R'''<sup>n</sup> halmazon értelmezett '''R'''<sup>m</sup>-be képező, az ''u'' ∈ ''H''-ban differenciálható függvények, akkor minden λ számra
| |
| − | :<math>\lambda.f\,</math> is differenciálható ''u''-ban és <math>\mathrm{d}(\lambda.f)(u)=\lambda.\mathrm{d}f(u)\,</math> és
| |
| − | :<math>f+g\,</math> is differenciálható ''u''-ban és <math>\mathrm{d}(f+g)(u)=\mathrm{d}f(u)+\mathrm{d}g(u)\,</math>
| |
| − | ''Ugyanis,'' a mondott differenciálokkal és a
| |
| − | :<math>\varepsilon_{\lambda.f}=\lambda.\varepsilon_{f}\,</math>
| |
| − | :<math>\varepsilon_{f+g}=\varepsilon_{f}+\varepsilon_{g}\,</math>
| |
| − | választással, ezek az ''u''-ban folytonosak lesznek és a lineáris résszekel együtt ezek előállítják a skalárszoros és összegfüggvények megváltozásait.
| |
| − | ===Függvénykompozíció differenciálja===
| |
| − | '''Tétel. ''' Legyen ''g'': '''R'''<sup>n</sup> ⊃<math>\to</math> '''R'''<sup>m</sup>, az ''u''-ban differenciálható, ''f'': '''R'''<sup>m</sup> ⊃<math>\to</math> '''R'''<sup>k</sup> a ''g''(''u'')-ban differenciálható függvény, ''u'' ∈ int Dom(''f'' <math>\circ</math> ''g''). Ekkor az
| |
| − | :<math>f\circ g</math> differenciálható ''u''-ban és
| |
| − | :<math> \mathrm{d}(f\circ g)(u)=\mathrm{d}f(g(u))\circ\mathrm{d}g(u)</math>
| |
| − |
| |
| − | ''Bizonyítás. '' Alkalmas ε, ''A'' és η ''B'' párral, minden ''x'' ∈ Dom(''f'' <math>\circ</math> ''g'')-re:
| |
| − | :<math>f(g(x))=f(g(u))+\mathcal{A}(g(x)-g(u))+\varepsilon(g(x))||g(x)-g(u)||)=</math>
| |
| − | ::<math>=f(g(u))+\mathcal{A}(\mathcal{B}(x-u)+\eta(x)||x-u||)+\varepsilon(g(x))||g(x)-g(u)||)=</math>
| |
| − | ::<math>=f(g(u))+(\mathcal{A}\circ\mathcal{B})(x-u)+\mathcal{A}(\eta(x)||x-u||)+\varepsilon(g(x))||g(x)-g(u)||)=</math>
| |
| − | ::<math>=f(g(u))+(\mathcal{A}\circ\mathcal{B})(x-u)+(\mathcal{A}(\eta(x))+\varepsilon(g(x))||\mathcal{B}\frac{x-u}{||x-u||}+\eta(x)||)||x-u||</math>
| |
| − | Innen leolvasható a differenciál és a másodrendben eltűnő mennyiség vektortényezője, az
| |
| − | :<math>\varepsilon_{f\circ g}(x)=\mathcal{A}(\eta(x))+\varepsilon(g(x))||\mathcal{B}\frac{x-u}{||x-u||}+\eta(x)||</math>
| |
| − | melyben az első tag a 0-hoz tart, mivel a lineáris leképezés a 0-ban folytonos, és η a 0-hoz tart az ''u''-ban. A második tag nulla szor korlátos alakú, hiszen a lineáris leképezés Lipschitz-tuladonsága folytán ''B'' minden egységvektoron korlátos értéket vesz fel.
| |
| − |
| |
| − | Ennek a tételnek a legegyszerűbb, de már vektorokat tartalmazó formáját írja át "fogyasztható" formába az alábbi
| |
| − |
| |
| − | '''Következmény.''' Ha ''g'': '''R'''<sup>n</sup> ⊃<math>\to</math> '''R''', az ''u''-ban differenciálható, ''f'': '''R''' ⊃<math>\to</math> '''R''' a ''g''(''u'')-ban differenciálható függvény, ''u'' ∈ int Dom(''f'' <math>\circ</math> ''g''), akkor
| |
| − | :<math>f\circ g</math> differenciálható ''u''-ban és
| |
| − | :<math> \mathrm{grad}(f\circ g)(u)=f'(g(u)).\mathrm{grad}\,g(u)</math>
| |
| − | Ahol . a skalárral való szorzást jelöli.
| |
| − |
| |
| − | ====1. Példa====
| |
| − | :<math>\Phi(\mathbf{r})=|\mathbf{r}|=\sqrt{\mathbf{r}^2}</math>
| |
| − | Először a gradienst számítjuk ki. Mivel a gyökfüggvény nem differenciálható a 0-ban, ezért a differenciál csak nemnulla '''r'''-re számítható ki. 0-ban a függvény tényleg nem differenciálható, mert a parciális deriváltak nem léteznek.
| |
| − | :<math>\Phi=\sqrt{.}\circ (.)^2\,</math>
| |
| − | és
| |
| − | :<math>\sqrt{.}\,'=\frac{1}{2\sqrt{.}}</math> illetve <math>\mathrm{grad}\, \mathbf{r}^2=2\mathbf{r}\,</math>
| |
| − | Ezért
| |
| − | :<math>\mathrm{grad}\,\Phi(\mathbf{r})=\sqrt{.}'(\mathbf{r}^2). \mathrm{grad}\,\mathbf{r}^2=\frac{1}{2\sqrt{\mathbf{r}^2}}\cdot 2\mathbf{r}=\frac{\mathbf{r}}{|\mathbf{r}|}</math>
| |
| − | Ha valakinek a differenciál leképezés kell, akkor pedig:
| |
| − | :<math>\mathrm{d}\sqrt{v}:y\mapsto \frac{1}{2\sqrt{v}}\cdot y </math>
| |
| − | :<math>v=\mathbf{r}^2\,</math>
| |
| − | :<math>\mathrm{d}\mathbf{r}^2:\mathbf{x}\mapsto 2\mathbf{r}\cdot \mathbf{x}</math>
| |
| − | Ezek kompozíciója:
| |
| − | :<math>\mathrm{d}\Phi(\mathbf{r}):\mathbf{x}\mapsto \frac{1}{2\sqrt{\mathbf{r}^2}}.2\mathbf{r}\cdot\mathbf{x}=\frac{\mathbf{r}}{|\mathbf{r}|}\cdot\mathbf{x}</math>
| |
| − | Szemléleti okokból lényeges, hogy itt . a skalárral való szorzás, <math>\cdot</math> a skaláris szorzás.
| |
| − |
| |
| − | ====2. Példa====
| |
| − | :<math>\Psi(\mathbf{r})=|\mathbf{r}|^{\alpha}</math>
| |
| − | :<math>\mathrm{d}\Psi(\mathbf{r}):\mathbf{x}\mapsto \alpha|\mathbf{r}|^{\alpha-1}.\frac{\mathbf{r}}{|\mathbf{r}|}\cdot\mathbf{x}</math>
| |
| − | illetve a gradiens:
| |
| − | :<math>\mathrm{grad}\,|\mathbf{r}|^\alpha=\alpha|\mathbf{r}|^{\alpha-1}.\frac{\mathbf{r}}{|\mathbf{r}|}</math>
| |
| − |
| |
| − | ===Folytonosság mint szükséges feltétel===
| |
| − | Ha ''f'' differenciálható ''u''-ban, akkor ott folytonos is, ugyanis minden ''x''-re:
| |
| − | :<math>f(x)=f(u)+(\mathrm{d}f(u))(x-u)+\varepsilon(x)||x-u||</math>
| |
| − | amely tagjai mind folytonosak ''u''-ban.
| |
| − |
| |
| − | ===Skalárfüggvények szorzata===
| |
| − | λ, μ: ''H'' <math>\to</math> '''R''', ahol ''H'' ⊆ '''R'''<sup>n</sup> és az ''u'' ∈ ''H''-ban mindketten differenciálhatók, akkor λμ is és
| |
| − | :<math>[\mathrm{d}(\lambda\mu)(u)]_{1j}=\partial_j(\lambda\mu)=\mu\partial_j\lambda+\lambda\partial_j\mu=[\mu(u).\mathrm{grad}\,\lambda(u)+\lambda(u).\mathrm{grad}\,\mu(u)]_{j}</math>
| |
| − | azaz
| |
| − | :<math>\mathrm{grad}(\lambda\mu)(u)=\mu(u).\mathrm{grad}\,\lambda(u)+\lambda(u).\mathrm{grad}\,\mu(u)</math>
| |
| − | ====Példa====
| |
| − | Számoljuk ki '''r'''<sup>2</sup> deriváltját a szorzat szabálya szerint.
| |
| − |
| |
| − | Egyrészt, ha '''r''' ≠ '''0''', akkor
| |
| − | :<math>\mathrm{grad}\,\mathbf{r}^2=\mathrm{grad}\,|\mathbf{r}|\cdot|\mathbf{r}|=2|\mathbf{r}|.\mathrm{grad}|\mathbf{r}|=2|\mathbf{r}|.\frac{\mathbf{r}}{|\mathbf{r}| } =2\mathbf{r}\,</math>
| |
| − |
| |
| − | Másrészt, ha '''r''' = '''0''', akkor
| |
| − | :<math> \mathbf{r}^2=0+\mathbf{0}\cdot\mathbf{r}+|\mathbf{r}|\cdot |\mathbf{r}|\,</math>
| |
| − | minden '''r'''-re fennáll, így grad('''id'''<sup>2</sup>)('''0''') = '''0''' alkalmas az ε('''r''')=|'''r'''|-rel, tehát '''r'''<sup>2</sup> differenciálható 0-ban is.
| |
| | | | |
| | <center> | | <center> |
| 150. sor: |
70. sor: |
| | |} | | |} |
| | </center> | | </center> |
| | + | |
| | + | [[Kategória:Matematika A2]] |
A többváltozós differenciálhatóságot az egyváltozós alábbi átfogalmazásából általánosítjuk:
így minden x = u + ty értékre is az azonosan nullát kapjuk, ha t pozitív szám, y pedig rögzített nemnulla vektor, azaz minden t-re
Erre vonatkozik a két alábbi példa.
 Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn
Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn  Rm lineáris leképezés, hogy
Rm lineáris leképezés, hogy
 Rm lineáris leképezés és ε: Dom(f)
Rm lineáris leképezés és ε: Dom(f)  Rm függvény, melyre:
Rm függvény, melyre:
 0 esetén szintén nulla:
0 esetén szintén nulla:
 0 esetén
ε és η nullává válik.
Ez viszont pont azt jelenti, hogy a két lineéris operátor azonosan egyenlő.
0 esetén
ε és η nullává válik.
Ez viszont pont azt jelenti, hogy a két lineéris operátor azonosan egyenlő.
 parciális differenciálhatóság
parciális differenciálhatóság
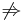 teljes differenciálhatóság
teljes differenciálhatóság
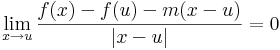

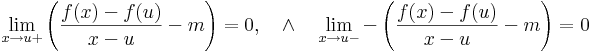
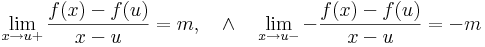
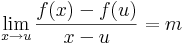
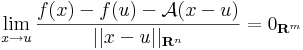
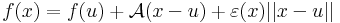
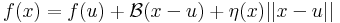
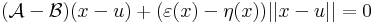
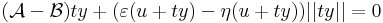
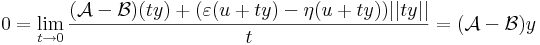
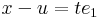
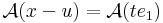
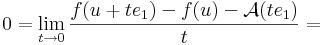
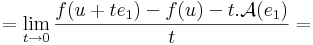
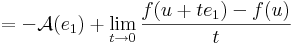
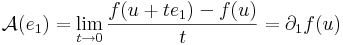
![[\mathrm{d}f(u)]=\mathbf{J}^f(u)=\begin{bmatrix}
\partial_1 f_1(u) & \partial_2 f_1(u) & \dots & \partial_n f_1(u)\\
\partial_1 f_2(u) & \partial_2 f_2(u) & \dots & \partial_n f_2(u)\\
\vdots & \vdots & \ddots & \vdots \\
\partial_1 f_m(u) & \partial_2 f_m(u) & \dots & \partial_n f_m(u)\\
\end{bmatrix}](/upload/math/b/c/8/bc8c1cf3c3d6f5032a7858552cc82a3a.png)