|
|
| (egy szerkesztő 2 közbeeső változata nincs mutatva) |
| 62. sor: |
62. sor: |
| | | | |
| | | | |
| − | ==Folytonosság és totális differenciálhatóság==
| |
| − | Tekintsük az
| |
| − | :<math>g(x,y)=\left\{\begin{matrix}\begin{pmatrix}\frac{xy}{x^2+y^2}\\ x+y\end{pmatrix}& \mbox{, ha }&(x,y)\ne (0,0)\\
| |
| − | \begin{pmatrix}0\\ 0\end{pmatrix}&\mbox{, ha }&(x,y)=(0,0)\end{matrix}\right.</math>
| |
| − | Ekkor
| |
| − | :<math>J^g(0,0)=\begin{pmatrix}0 & 0\\
| |
| − | 1 & 1\end{pmatrix}</math>
| |
| − | Viszont g nem totálisan diffható, mert a (t,t) mentén a (0,0)-ba tartva:
| |
| − | :<math>\lim\limits_{t\to 0}\frac{g(t,t)-g(0,0)-J^g(0,0)\cdot(t,t)}{\sqrt{2}|t|}=\lim\limits_{t\to 0}\frac{(\frac{1}{2},2t)-(0,t)}{\sqrt{2}|t|}=\lim\limits_{t\to 0}\frac{(\frac{1}{2},t)}{\sqrt{2}|t|}=\lim\limits_{t\to 0}(\frac{1}{\sqrt{2}2|t|},\frac{t}{\sqrt{2}|t|})</math>
| |
| − | ami nem létezik.
| |
| − |
| |
| − | '''Megjegyzés.''' Itt persze g nem folytonos, és itt is igaz az, hogy ha totálisan differenciálható egy függvény, akkor folytonos is:
| |
| − |
| |
| − | '''Tétel.''' Ha ''f'' differenciálható ''u''-ban, akkor ott folytonos is, ugyanis minden ''x''-re:
| |
| − | :<math>f(x)=f(u)+(\mathrm{d}f(u))(x-u)+\varepsilon(x)||x-u||</math>
| |
| − | amely tagjai mind folytonosak ''u''-ban.
| |
| − |
| |
| − | ==Iránymenti deriválhatóság és differenciálhatóság==
| |
| − | '''Példa.'''
| |
| − | :<math>f(x,y)=\left\{\begin{matrix}\frac{xy}{\sqrt{x^2+y^2}}& \mbox{, ha }&(x,y)\ne (0,0)\\
| |
| − | 0&\mbox{, ha }&(x,y)=(0,0)\end{matrix}\right.</math>
| |
| − |
| |
| − | Ekkor
| |
| − | :<math>\mathrm{J}^f(0,0)=[0, 0]\,</math>
| |
| − |
| |
| − | Ha tehát differenciálható, akkor az '''iránymenti derivált'''ak (Gateau-deriváltak) is léteznek (e egységvektor):
| |
| − |
| |
| − | :<math>\partial_ef(u)=\lim\limits_{t\to 0}\frac{f(u+te)-f(u)}{t}=\mathrm{J}^f(0,0)\cdot e=e\cdot\mathrm{grad}\,f(u)</math>
| |
| − |
| |
| − | Ám, polárkoordinátákra áttérve:
| |
| − | :<math>f(x(r,\varphi),y(r,\varphi))=\frac{r^2\cos\varphi\sin\varphi}{r}=r\cos\varphi\sin\varphi=r\cdot \frac{1}{2}\sin 2\varphi</math>
| |
| − | φ = π/4-et és π + π/4-et véve a vetületfüggvény a
| |
| − | :<math>t\mapsto\frac{1}{2}|t|</math>,
| |
| − | ami nem differenciálható a 0-ban.
| |
| − |
| |
| − | '''Megjegyzés.''' Persze abból, hogy az összes iránymenti derivált létezik, abból nem következik, hogy a függvény totálisan deriválható:
| |
| − | ==Folytonos parciális differenciálhatóság==
| |
| − |
| |
| − | Megfordításról a következő esetben beszélhetünk.
| |
| − |
| |
| − | '''Tétel.''' Ha az ''f'':'''R'''<sup>n</sup> ⊃<math>\to</math> '''R'''<sup>m</sup> függvény minden parciális deriváltfüggvénye létezik az ''u'' egy környezetében és ''u''-ban a parciális deriváltak folytonosak, akkor ''u''-ban ''f'' differenciálható. (Sőt, folytonosan differenciálható.)
| |
| − |
| |
| − | ''Bizonyítás.'' Elegendő az m = 1 esetet vizsgálni. Továbbá a bizonyítás elve nem változik, ha csak az n = 2 esetet tekintjük. Legyen x az u mondott környezetéből vett pont, és x = (<math>x_1</math>,<math>x_2</math>), v=(<math>u_1</math>,<math>x_2</math>), u=(<math>u_1</math>,<math>u_2</math>) Ekkor az [x,v] szakaszon ∂<sub>1</sub>f-hez a Lagrange-féle középértéktétel miatt létezik olyan ξ(<math>x_1</math>)∈[<math>x_1</math>,<math>u_1</math>] szám, és a [v,u] szakaszon ∂<sub>2</sub>f-hez ζ(<math>x_2</math>)∈[<math>x_2</math>,<math>u_2</math>] szám, hogy
| |
| − | :<math>f(x)-f(u)=f(x)-f(v)+f(v)-f(u)=\,</math>
| |
| − | :<math>=\partial_1 f(\xi(x_1),x_2)(x_1-u_1)+\partial_2 f(u_1,\zeta(x_2))(x_2-u_2)=</math>
| |
| − | :<math>=\partial_1f(u)(x_1-u_1)+\partial_2f(u)(x_2-u_2)+</math>
| |
| − | :<math>+(\partial_1 f(\xi(x_1),x_2)-\partial_1f(u))(x_1-u_1)+(\partial_2 f(u_1,\zeta(x_2))-\partial_2f(u))(x_2-u_2)</math>
| |
| − | itt az
| |
| − | :<math>\varepsilon_1(x)=\partial_1 f(\xi(x_1),x_2)-\partial_1f(u)</math> és <math>\varepsilon_2(x)=\partial_2 f(x_1,\zeta(x_2))-\partial_2f(u)</math>
| |
| − | függvények folytonosak ''u''-ban (még ha a ξ, ζ függvények nem is azok), és értékük az ''u''-ban 0. Világos, hogy ez azt jelenti, hogy f differenciálható ''u''-ban.
| |
| − |
| |
| − | Világos, hogy a parciális deriváltak folytonossága szükséges a fenti tételben. Az alábbi példában léteznek a parciális deriváltfüggvények az ''u'' egy környzetében, de az ''u''-ban nem folytonosak.
| |
| − | ====Nem differenciálható, nem folytonosan parciálisan differenciálható függvény====
| |
| − |
| |
| − | :<math>f(x,y)=\left\{\begin{matrix}\frac{xy}{\sqrt{x^2+y^2}}& \mbox{, ha }&(x,y)\ne (0,0)\\
| |
| − | 0&\mbox{, ha }&(x,y)=(0,0)\end{matrix}\right.</math>
| |
| − | parciális deriváltfüggvényei léteznek:
| |
| − | :<math>\frac{\partial f(x,y)}{\partial x}=\frac{y}{\sqrt{x^2+y^2}}-\frac{x^2y}{\sqrt{(x^2+y^2)^3}}</math>
| |
| − | a másik hasonlóan. A 0-ban 0 mindkettő, de az (0,1/n) mentén a 0-ba tartva az 1-hez tart, ami nem 0.
| |
| − |
| |
| − | :<math>f(x,y)=\left\{\begin{matrix}
| |
| − | 0,& \mbox{ ha }(x,y)=(0,0)\\
| |
| − | \frac{xy(x^2-y^2)}{x^2+y^2},& \mbox{ ha }(x,y)\ne(0,0)
| |
| − | \end{matrix}\right.</math>
| |
| − | A Young-tételnél beláttuk, hogy ekkor a 0-ban nem egyenlő a két vegyes parciális derivált. Most már azt is tudjuk miért. A függvény gradiense nem differenciálható totálisan a 0-ban. Ehhez elevenítsük föl, hogy
| |
| − |
| |
| − | :<math>J^g(0,0)=H^f(0,0)=\begin{bmatrix}
| |
| − | 0 & -1\\
| |
| − | 1 & 0
| |
| − | \end{bmatrix}</math>
| |
| − | ami a 90˚-os forgatás.
| |
| − |
| |
| − | Számoljuk ki g értékét a (x,x) alakú pontokban:
| |
| − |
| |
| − | :<math>\partial_1f(x,x)=\lim\limits_{t\to 0}\frac{f(x+t,x)-f(0,0)}{t}=\lim\limits_{t\to 0}\frac{(x+t)x((x+t)^2-x^2)}{t((x+t)^2+x^2)}=</math>
| |
| − | :<math>\lim\limits_{t\to 0}\frac{(x+t)x(2tx+t^2)}{t(2x^2+2tx+t^2)}=\lim\limits_{t\to 0}\frac{(x+t)x(2x+t)}{2x^2+2tx+t^2}=\lim\limits_{t\to 0}=x</math>
| |
| − | :<math>\partial_2f(x,x)=\lim\limits_{t\to 0}\frac{f(x,x+t)-f(0,0)}{t}=\lim\limits_{t\to 0}\frac{x(x+t)(x^2-(x+t)^2)}{t(x^2+(x+t)^2)}=</math>
| |
| − | :<math>\lim\limits_{t\to 0}\frac{x(x+t)(-2tx-t^2)}{t(2x^2+2tx+t^2)}=-x</math>
| |
| − |
| |
| − | Tehát g(t,t)=(t,-t), és emiatt
| |
| − |
| |
| − | :<math>\lim\limits_{t\to 0}\frac{g(t,t)-g(0,0)-J^g(0,0)\cdot (t,t)}{|t|}=\lim\limits_{t\to 0}\frac{(t,-t)-(-t,t)}{|t|}=\lim\limits_{t\to 0}\frac{(2t,-2t)}{|t|}=\lim\limits_{t\to 0}(2\mathrm{sgn}(t),-2\mathrm{sgn}(t))\ne (0,0)\,</math>
| |
| − | márpedig ha g minden parciális deriváltja folytonos lenne a (0,0)-ban, akkor g totálisan is deriválható lenne.
| |
| − |
| |
| − | ====Differenciálható, de nem folytonosan parciálisan differenciálható====
| |
| − | A differenciálhatóság azonban nem elég ahhoz, hogy a parciális deriváltak folytonosak legyenek.
| |
| − |
| |
| − | Az
| |
| − | :<math>f(x,y)=\left\{\begin{matrix}(x^2+y^2)\sin\cfrac{1}{x^2+y^2}, & \mbox{ha} & (x,y)\ne (0,0)\\\\
| |
| − | 0, & \mbox{ha} & (x,y) =(0,0)
| |
| − | \end{matrix}\right.
| |
| − | </math>
| |
| − | differenciálható, hiszen ez az
| |
| − | :<math>f(\mathbf{r})=\left\{\begin{matrix} \mathbf{r}^2\cdot\sin(|\mathbf{r}|^{-2}) & \mbox{ha} & \mathbf{r}\ne \mathbf{0}\\\\
| |
| − | \mathbf{0}, & \mbox{ha} & \mathbf{r}= \mathbf{0}\end{matrix}\right.
| |
| − | </math>
| |
| − | függvény és '''r''' ≠ '''0'''-ban:
| |
| − | :<math>\mathrm{grad}(f)=\sin(|\mathbf{r}|^{-2}).\mathrm{grad}\,\mathbf{r}^2+\mathbf{r}^2.\mathrm{grad}\,\sin(|\mathbf{r}|^{-2})=</math>
| |
| − | :<math>=\sin(|\mathbf{r}|^{-2}).2\mathbf{r}+\mathbf{r}^2\cdot\cos(|\mathbf{r}|^{-2})\cdot(-2)|\mathbf{r}|^{-3}.\frac{\mathbf{r}}{|\mathbf{r}|}</math>
| |
| − | és grad f nem korlátos. Ez persze a parciális deriváltakon is megátszik: azok sem korlátosak.
| |
| − |
| |
| − | ==Egyváltozós illetve valós értékű függvény deriváltja==
| |
| − |
| |
| − | Ha f:'''R'''<sup>n</sup> <math>\supset\!\to</math> '''R''', akkor a definíciót még így is ki szokás mondani:
| |
| − |
| |
| − | f diffható ''r''<sub>0</sub>-ban, ha létezik ''m'' vektor, hogy
| |
| − | :<math>\lim\limits_{r\to r_0}\frac{f(r)-f(r_0)-m\cdot(r-r_0)}{|r-r_0|}=0</math>
| |
| − |
| |
| − | Ekkor az m a '''gradiensvektor''', melynek sztenderd bázisbeli koordinátamátrixa a Jacobi mátrix:
| |
| − | :<math>\mathrm{grad}\,f(r_0)=[\partial_1f(r_0),...,\partial_nf(r_0)]</math>
| |
| − |
| |
| − | Ha f:'''R''' <math>\supset\!\to</math> '''R'''<sup>n</sup>, akkor a definíciót még így is ki szokás mondani:
| |
| − | :<math>\exists\,f'(t_0)=\lim\limits_{t\to t_0}\frac{f(t)-f(t_0)}{t-t_0}\,</math>
| |
| − | és ekkor f'(<math>t_0</math>) a <math>t_0</math>-beli '''deriváltvektor''' (ha t az idő és r=f(t) a hely, akkor ez a sebeségvektor).
| |
| − |
| |
| − | Ha f:'''R'''<sup>n</sup> <math>\supset\!\to</math> '''R'''<sup>n</sup>, akkor a differenciált '''deriválttenzor'''nak is nevezik.
| |
| − |
| |
| − |
| |
| − | '''Példa.'''
| |
| − |
| |
| − | Mi az
| |
| − | :<math>f(r)=r^2\,</math>,
| |
| − | skalárfüggvény gradiense?
| |
| − |
| |
| − | Válasszuk le a lineáris részét!
| |
| − |
| |
| − | :<math>r^2-r_0^2=(r-r_0)(r+r_0)=(r-r_0)(2r_0+r-r_0)=2r_0\cdot(r-r_0)+(r-r_0)^2\,</math>
| |
| − | Itt az első tag a lineáris, a második a magasabbfokú. Tehát:
| |
| − | :<math>\mathrm{grad}\,r^2=2r\,</math>
| |
| − |
| |
| − | ==Lineáris és affin függvény deriváltja==
| |
| − | '''Tétel.''' Az ''A'' : '''R'''<sup>n</sup> <math>\to</math> '''R'''<sup>m</sup> lineáris leképezés differenciálható és differenciálja minden pontban saját maga:
| |
| − | :<math>\mathrm{d}\mathcal{A}(u)=\mathcal{A}\,</math>
| |
| − |
| |
| − | ''Ugyanis, '' legyen ''u'' ∈ '''R'''<sup>n</sup>. Ekkor
| |
| − |
| |
| − | :<math>\lim\limits_{x\to u}\frac{\mathcal{A}(x)-\mathcal{A}(u)-\mathcal{A}(x-u)}{||x-u||}=\lim\limits_{x\to u}0=0</math>
| |
| − |
| |
| − | '''Tétel.''' Az azonosan '''c''' konstans függény esetén az d''c''(''u'') <math>\equiv</math> 0 alkalmas differenciálnak, mert
| |
| − | :<math>\lim\limits_{x\to u}\frac{c-c-0\cdot(x-u)}{||x-u||}=\lim\limits_{x\to u}0=0</math>
| |
| − |
| |
| − |
| |
| − | '''Tétel.''' Ha ''f'' és ''g'' a ''H'' ⊆ '''R'''<sup>n</sup> halmazon értelmezett '''R'''<sup>m</sup>-be képező, az ''u'' ∈ ''H''-ban differenciálható függvények, akkor minden λ számra
| |
| − | :<math>\lambda.f\,</math> is differenciálható ''u''-ban és <math>\mathrm{d}(\lambda.f)(u)=\lambda.\mathrm{d}f(u)\,</math> és
| |
| − | :<math>f+g\,</math> is differenciálható ''u''-ban és <math>\mathrm{d}(f+g)(u)=\mathrm{d}f(u)+\mathrm{d}g(u)\,</math>
| |
| − | ''Ugyanis,'' a mondott differenciálokkal és a
| |
| − | :<math>\varepsilon_{\lambda.f}=\lambda.\varepsilon_{f}\,</math>
| |
| − | :<math>\varepsilon_{f+g}=\varepsilon_{f}+\varepsilon_{g}\,</math>
| |
| − | választással, ezek az ''u''-ban folytonosak lesznek és a lineáris résszekel együtt ezek előállítják a skalárszoros és összegfüggvények megváltozásait.
| |
| − |
| |
| − | '''Következmény.''' Tehát minden ''u'' ∈ '''R'''<sup>n</sup>-re az '''affin''' c+''A'' diffható és
| |
| − | :<math>\mathrm{d}(c+\mathcal{A})(u)=\mathcal{A}</math>
| |
| − |
| |
| − | ===Példa===
| |
| − |
| |
| − | Az ''A'': '''x''' <math>\mapsto</math> 2<math>x_1</math> + 3<math>x_2</math> - 4<math>x_3</math> lineáris leképezés differenciálja az '''u''' pontban az '''u'''-tól független
| |
| − | :<math>(\mathrm{d}\mathcal{A}(\mathbf{u}))(x_1,x_2,x_3)=2x_1+3x_2-4x_3\,</math>
| |
| − | és Jacobi-mátrixa a konstans
| |
| − | :<math>\mathbf{J}^\mathcal{A}(\mathbf{u})=\begin{bmatrix}2 & 3 & -4\end{bmatrix}</math>
| |
| − | mátrix.
| |
| − |
| |
| − | Világos, hogy a
| |
| − | :<math>\mathrm{pr}_i:(x_1,x_2,...,x_i,...,x_n)\mapsto x_i</math>
| |
| − | koordináta vagy projekciófüggvény lineáris, differenciálja minden '''u''' pontban saját maga és ennek mátrixa:
| |
| − | :<math>[\mathrm{grad}\,\mathrm{pr_i}]=\mathbf{J}^{\mathrm{pr}_i}(\mathbf{u})=\begin{bmatrix}0 & 0 & ... & 1 & ...& 0\end{bmatrix}</math>
| |
| − | ahol az 1 az i-edik helyen áll. Másként
| |
| − | :<math>\partial_kx_i=\delta_{ki}</math>
| |
| − | ahol
| |
| − | :<math>\delta_{ij}=\left\{\begin{matrix}1, \mbox{ ha }i=j\\0, \mbox{ ha }i\ne j \end{matrix}\right.</math>
| |
| − | azaz a Kronecker-féle δ szimbólum.
| |
| − |
| |
| − |
| |
| − | ==Szélsőérték szükséges feltétele==
| |
| − |
| |
| − | Egyelőre állapodjunk meg abban, hogy gradiensnek nevezzük a következő többváltozós vektorértékű függvényt: ha ''f'': '''R'''<sup>n</sup> <math>\supset\!\to</math> '''R''' parciálisan differenciálható, akkor
| |
| − | :<math>\mathrm{grad}\,f(x)=(\partial_1f(x),...,\partial_nf(x))</math>
| |
| − | mely lényegében az ''f'' elsőrendű parciális deriváltjaiból képezett vektor.
| |
| − |
| |
| − | Később a gradienst egy kissé másképp fogjuk értelmezni és amit most definiáltunk, az a gradiens sztenderd bázisbeli mátrixa lesz (adott pontra vonatkozóan).
| |
| − |
| |
| − |
| |
| − | '''Tétel''' - ''Fermat-tétel'' - Legyen ''f'': '''R'''<sup>n</sup> <math>\supset\!\to</math> '''R''', ''u'' ∈ int Dom(''f''), ''f'' parciálisan differenciálható ''u''-ban.
| |
| − | :Ha ''u''-ban ''f''-nek (lokális) szélsőértéke van, akkor
| |
| − | ::<math>\mathrm{grad}\,f(u)=0_{\mathbf{R}^n}\,</math>
| |
| − | ''U.is:'' minden ''i''-re az ''i''-edik parciális függvénynek szélsőértéke van ''u''<sub>i</sub>-ben, így az egyváltozós Fermat-tétel miatt ezeknek a deriváltja ''u''<sub>i</sub>-ben 0, így a gradiens értéke 0.
| |
| − |
| |
| − | ====Példa====
| |
| − | :<math>f(x,y)=x^2y^2\,</math>
| |
| − | Ennek gradiense:
| |
| − | :<math>\mathrm{grad}\,f(x,y)=(2xy^2,2yx^2)</math>
| |
| − | Az
| |
| − | :<math>\left.
| |
| − | \begin{matrix}
| |
| − | \mathrm{I.} & 2xy^2 & = & 0\\
| |
| − | \mathrm{II.} & 2yx^2 & = & 0\\
| |
| − | \end{matrix}
| |
| − | \right\}</math>
| |
| − | egyenletrendszer megoldásai: ''x'' = 0, ''y'' tetszőleges ill. ''y'' = 0 és ''x'' tetszőleges. A szélsőértékek helyei csak ezek közül kerülhetnek ki és ezek valóban szélsőértékek is, mert ezeken a függvény 0-t vesz fel, ami a lehetséges legkisebb értéke.
| |
| − | :<gnuplot>
| |
| − | set pm3d
| |
| − | set size 0.8,0.8
| |
| − | set xrange [-1:1]
| |
| − | set yrange [-1:1]
| |
| − | set zrange [-2:2]
| |
| − | set view 50,30,1,1
| |
| − | unset xtics
| |
| − | unset ytics
| |
| − | unset ztics
| |
| − | unset key
| |
| − | unset colorbox
| |
| − | splot 5*x*x*y*y
| |
| − | </gnuplot>
| |
| − |
| |
| − | ==Magasabbrendű parciális deriváltak==
| |
| − | Ha ''f'' parciálisan deriválható, akkor ∂<sub>1</sub>''f'' és ∂<sub>2</sub>''f'' szintén kétváltozós függvények (a pontonként a deriváltak, mint függvényértékek értelmezésével) és érdeklődhetünk ezek parciális differenciálhatóságuk iránt. Például:
| |
| − |
| |
| − | :<math>f(x,y)=x^2y^4+x^5-y^3\,</math>
| |
| − |
| |
| − | :<math>\partial_xf(x,y)=xy^4+5x^4</math>
| |
| − | :<math>\partial_yf(x,y)=x^24y^3-3y^2</math>
| |
| − |
| |
| − | :<math>\partial_x(\partial_xf)(x,y)=y^4+20x^3</math>
| |
| − | :<math>\partial_y(\partial_yf)(x,y)=12x^2y^2-6y^2</math>
| |
| − | :<math>\partial_y(\partial_xf)(x,y)=x4y^3</math>
| |
| − | :<math>\partial_x(\partial_yf)(x,y)=4xy^3</math>
| |
| − |
| |
| − | És valóban:
| |
| − |
| |
| − | '''Tétel.''' (Young-tétel) Ha a másodrendű parciláis deriváltak léteznek az ''u'' egy környezetében és folytonosak az ''u'' pontban, akkor az ''u''-beli vegyes másodrendű parciláis deriváltak egyenlőek:
| |
| − | :<math>\partial_x(\partial_y f)(u)=\partial_y(\partial_x f)(u)</math>
| |
| − |
| |
| − | Azaz az alábbi, úgy nevezett Hesse-mátrix szimmetrikus:
| |
| − | :<math>H^f(u)=\begin{bmatrix}
| |
| − | \cfrac{\partial^2 f(u)}{\partial x^2} & \cfrac{\partial^2 f(u)}{\partial y\partial x}\\\\
| |
| − | \cfrac{\partial^2 f(u)}{\partial x\partial y} & \cfrac{\partial^2 f(u)}{\partial y^2}
| |
| − | \end{bmatrix}</math>
| |
| − |
| |
| − | '''Feladat.''' Az a kitétel, hogy az ''u''-ban a másodrenrű parciláis deriváltak folytonosak, nem hagyható el, ugyanis. Legyen
| |
| − | :<math>f(x,y)=\left\{\begin{matrix}
| |
| − | 0,& \mbox{ ha }(x,y)=(0,0)\\
| |
| − | \frac{xy(x^2-y^2)}{x^2+y^2},& \mbox{ ha }(x,y)\ne(0,0)
| |
| − | \end{matrix}\right.</math>
| |
| − | Ekkor a 0-ban nem egyenlő a két vegyes parciális derivált.
| |
| − |
| |
| − | Tekintsük a parciális deriváltakat:
| |
| − | :<math>\partial_x(\partial_yf)(0,0)=\lim\limits_{x\to 0}\frac{(\partial_yf)(x,0)-(\partial_yf)(0,0)}{x}</math>
| |
| − | :<math>\partial_y(\partial_xf)(0,0)=\lim\limits_{y\to 0}\frac{(\partial_xf)(0,y)-(\partial_xf)(0,0)}{y}</math>
| |
| − | :<math>\partial_x(\partial_xf)(0,0)=\lim\limits_{x\to 0}\frac{(\partial_xf)(x,0)-(\partial_xf)(0,0)}{x}</math>
| |
| − | :<math>\partial_y(\partial_yf)(0,0)=\lim\limits_{y\to 0}\frac{(\partial_yf)(0,y)-(\partial_yf)(0,0)}{y}</math>
| |
| − | Ehhez tehát elegendő kiszámítani a következő föggvényeket: y <math>\mapsto</math> (∂<sub>x</sub>f)(0,y), x <math>\mapsto</math> (∂<sub>y</sub>f)(x,0). Ehhez a parciális deriváltak:
| |
| − | :<math>\partial_xf(0,y)=\lim\limits_{t\to 0}\frac{f(t,y)-f(0,0)}{t}=\left\{\begin{matrix}
| |
| − | 0,& \mbox{ ha }y=0\\
| |
| − | -y,& \mbox{ ha }y\ne 0
| |
| − | \end{matrix}\right.</math>
| |
| − | :<math>\partial_yf(x,0)=\lim\limits_{t\to 0}\frac{f(x,t)-f(0,0)}{t}=\left\{\begin{matrix}
| |
| − | 0,& \mbox{ ha }x=0\\
| |
| − | x,& \mbox{ ha }x\ne 0
| |
| − | \end{matrix}\right.</math>
| |
| − | :<math>\partial_yf(0,y)=\lim\limits_{t\to 0}\frac{f(0,y+t)-f(0,0)}{t}=0</math>
| |
| − | :<math>\partial_xf(x,0)=\lim\limits_{t\to 0}\frac{f(x+t,0)-f(0,0)}{t}=0</math>
| |
| − |
| |
| − | Megjegyezzük, hogy a g=(∂<sub>x</sub>f,∂<sub>y</sub>f) függvény (0,0)-beli parciális deriváltjai nem lehetnek folytonosak, mert ott a függvény nem totálisan diffható. Ugyanis a g Jacobi-mátrixa:
| |
| − | :<math>J^g(0,0)=H^f(0,0)=\begin{bmatrix}
| |
| − | 0 & -1\\
| |
| − | 1 & 0
| |
| − | \end{bmatrix}</math>
| |
| − | ami a 90˚-os forgatás. Ekkor a g-t a (t,0) vektorral közelítve a 0-ba:
| |
| − | :<math>\lim\limits_{t\to 0}\frac{g(t,0)-g(0,0)-J^g(0,0)\cdot (t,0)}{|t|}=\lim\limits_{t\to 0}\frac{(0,-t)}{|t|}\ne (0,0)\,</math>
| |
| − | márpedig ha g minden parciális deriváltja folytonos lenne a (0,0)-ban, akkor g totálisan is deriválható lenne.
| |
| − |
| |
| − | ==Többváltozós függvény szélsőértéke==
| |
| − |
| |
| − |
| |
| − | ===Másodikderivált próba===
| |
| − | Kétszer differenciálható függvényre vonatkozóan megfogalmazhatjuk a lokális maximum és minimum létezésének elégséges feltételét. Csak a kétváltozós függvényekkel foglalkozunk. Tegyük fel, hogy grad ''f''(u) = 0 és H<sup>f</sup>(u) az ''f'' Hesse-mátrixa
| |
| − | # ha det H<sup>f</sup>(u) > 0 és ∂<sub>11</sub>''f''(''u'') < 0, akkor ''f''-nek ''u''-ban '''maximuma''' van
| |
| − | # ha det H<sup>f</sup>(u) > 0 és ∂<sub>11</sub>''f''(''u'') > 0, akkor ''f''-nek ''u''-ban '''minimuma''' van
| |
| − | # ha det H<sup>f</sup>(u) < 0, akkor ''f''-nek biztosan nincs szélsőértéke, ún. '''nyeregpont'''ja van
| |
| − | # ha det H<sup>f</sup>(u) = 0, akkor a próba nem járt sikerrel, azaz további vizsgálatokat igényel annak eldöntése, hogy ''u'' szélsőérték hely-e.
| |
| − |
| |
| − | ''Megjegyzések.'' Mivel kétváltozós esetben
| |
| − | :<math>\mathrm{det}\,\mathrm{H}^f(u)=\partial_{11}f(u)\cdot \partial_{22}f(u)-(\partial_{12}f(u))^2</math>
| |
| − | ezért olyan eset nem létezik, hogy det H<sup>f</sup>(u) > 0 és ∂<sub>11</sub>''f''(''u'') = 0.
| |
| − |
| |
| − | Világos, hogy a másodikderivált tipikusan azoknál a függvényeknél jár sikerrel, melyeket egy másodfokú függvény közelít a legjobban (aszimptotikusan másodfokúak). Ha a függvény ennél magasabb fokú, akkor a második deriváltak eltűnnek és a Hesse-mártix elfajul (vagy legalább is tipikusan elfajul).
| |
| − |
| |
| − | Ha tehát
| |
| − | :<math>\mathrm{H}^{f}(u)=\begin{pmatrix}
| |
| − | A & B \\
| |
| − | B & C
| |
| − | \end{pmatrix}</math>, akkor <math>\mathrm{det\,H}^{f}(u)=AC - B^2 </math>,
| |
| − | és így a tipikus példák a következők.
| |
| − |
| |
| − | ====Példák====
| |
| − |
| |
| − | '''1.''' Ha B kicsi, azaz az AC-hez képest kis abszolútrétékű szám, akkor a szélsőérték irányába mozdul el a feladat.
| |
| − | :<math>f(x,y)=x^2+xy+y^2\,</math>
| |
| − |
| |
| − | Ekkor grad ''f'' = ( 2x + y , 2y + x ) és
| |
| − | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix}
| |
| − | 2 & 1 \\
| |
| − | 1 & 2
| |
| − | \end{pmatrix}</math>
| |
| − | azaz 4 - 1 = 3 > 0 és 2 > 0 miatt minimum.
| |
| − | :<gnuplot>
| |
| − | set pm3d
| |
| − | set size 0.8,0.8
| |
| − | set xrange [-1:1]
| |
| − | set yrange [-1:1]
| |
| − | set zrange [-2:2]
| |
| − | set view 50,30,1,1
| |
| − | unset xtics
| |
| − | unset ytics
| |
| − | unset ztics
| |
| − | unset key
| |
| − | unset colorbox
| |
| − | splot x*x+x*y+y*y
| |
| − | </gnuplot>
| |
| − |
| |
| − | '''2.''' Ha |B| nagy (azaz AC-hez képest nagy), akkor a bizonyosan nemszélsőérték irányába.
| |
| − | :<math>f(x,y)=x^2-3xy+y^2\,</math>
| |
| − |
| |
| − | Ekkor grad ''f'' = ( 2x + -3y , 2y + -3x ) és
| |
| − | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix}
| |
| − | 2 & -3 \\
| |
| − | -3 & 2
| |
| − | \end{pmatrix}</math>
| |
| − | azaz 4 - 9 = -5 < 0 miatt nincs szélsőérték: nyeregpont.
| |
| − | :<gnuplot>
| |
| − | set pm3d
| |
| − | set size 0.8,0.8
| |
| − | set xrange [-1:1]
| |
| − | set yrange [-1:1]
| |
| − | set zrange [-2:2]
| |
| − | set view 50,30,1,1
| |
| − | unset xtics
| |
| − | unset ytics
| |
| − | unset ztics
| |
| − | unset key
| |
| − | unset colorbox
| |
| − | splot x*x -3*x*y+y*y
| |
| − | </gnuplot>
| |
| − |
| |
| − | '''3.''' Negatív A és C-re és kis B-re:
| |
| − | :<math>f(x,y)=-x^2+xy-y^2\,</math>
| |
| − |
| |
| − | Ekkor grad ''f'' = ( -2x + 3y , -2y + 3x ) és
| |
| − | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix}
| |
| − | -2 & 1 \\
| |
| − | 1 & -2
| |
| − | \end{pmatrix}</math>
| |
| − | azaz 4 - 1 = 3 > 0 és -2 < 0 miatt maximum.
| |
| − | :<gnuplot>
| |
| − | set pm3d
| |
| − | set size 0.8,0.8
| |
| − | set xrange [-1:1]
| |
| − | set yrange [-1:1]
| |
| − | set zrange [-2:2]
| |
| − | set view 50,30,1,1
| |
| − | unset xtics
| |
| − | unset ytics
| |
| − | unset ztics
| |
| − | unset key
| |
| − | unset colorbox
| |
| − | splot -x*x +x*y-y*y
| |
| − | </gnuplot>
| |
| − |
| |
| − | '''4.''' Ha A és C előjele ellenkező, akkor rögtön következik, hogy nincs sz.é.
| |
| − | :<math>f(x,y)=x^2+xy-y^2\,</math>
| |
| − |
| |
| − | Ekkor grad ''f'' = ( 2x + y , -2y + x ) és
| |
| − | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix}
| |
| − | 2 & 1 \\
| |
| − | 1 & -2
| |
| − | \end{pmatrix}</math>
| |
| − | azaz -4 - 1 = -5 < 0 azaz nyeregpont.
| |
| − | :<gnuplot>
| |
| − | set pm3d
| |
| − | set size 0.8,0.8
| |
| − | set xrange [-1:1]
| |
| − | set yrange [-1:1]
| |
| − | set zrange [-2:2]
| |
| − | set view 50,30,1,1
| |
| − | unset xtics
| |
| − | unset ytics
| |
| − | unset ztics
| |
| − | unset key
| |
| − | unset colorbox
| |
| − | splot x*x +x*y-y*y
| |
| − | </gnuplot>
| |
| − |
| |
| − | '''5.''' Atipikus eset, ha AC = B<sup>2</sup>. Ekkor nem jár sikerrel a próba:
| |
| − | :<math>f(x,y)=x^2+2xy+y^2\,</math>
| |
| − |
| |
| − | Ekkor grad ''f'' = ( 2x + 2y , 2y + 2x ) és
| |
| − | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix}
| |
| − | 2 & 2 \\
| |
| − | 2 & 2
| |
| − | \end{pmatrix}</math>
| |
| − | azaz 4 - 4 = 0, azaz határozatlan eset.
| |
| − | De tudjuk, hogy
| |
| − | :<math>f(x,y)=(x+y)^2\,</math>
| |
| − | ami pontosan akkor minimális, ha x = -y, azaz ezeken a helyeken van szélsőérték.
| |
| − | :<gnuplot>
| |
| − | set pm3d
| |
| − | set size 0.8,0.8
| |
| − | set xrange [-1:1]
| |
| − | set yrange [-1:1]
| |
| − | set zrange [-2:2]
| |
| − | set view 50,30,1,1
| |
| − | unset xtics
| |
| − | unset ytics
| |
| − | unset ztics
| |
| − | unset key
| |
| − | unset colorbox
| |
| − | splot (x+y)*(x+y)
| |
| − | </gnuplot>
| |
| | | | |
| | | | |
A többváltozós differenciálhatóságot az egyváltozós alábbi átfogalmazásából általánosítjuk:
így minden x = u + ty értékre is az azonosan nullát kapjuk, ha t pozitív szám, y pedig rögzített nemnulla vektor, azaz minden t-re
Erre vonatkozik a két alábbi példa.
 Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn
Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn  Rm lineáris leképezés, hogy
Rm lineáris leképezés, hogy
 Rm lineáris leképezés és ε: Dom(f)
Rm lineáris leképezés és ε: Dom(f)  Rm függvény, melyre:
Rm függvény, melyre:
 0 esetén szintén nulla:
0 esetén szintén nulla:
 0 esetén
ε és η nullává válik.
Ez viszont pont azt jelenti, hogy a két lineéris operátor azonosan egyenlő.
0 esetén
ε és η nullává válik.
Ez viszont pont azt jelenti, hogy a két lineéris operátor azonosan egyenlő.
 parciális differenciálhatóság
parciális differenciálhatóság
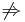 teljes differenciálhatóság
teljes differenciálhatóság
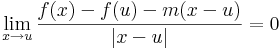

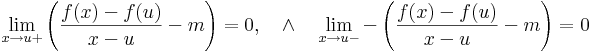
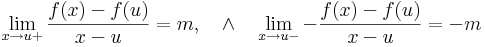
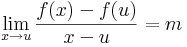
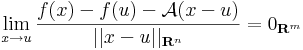
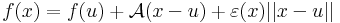
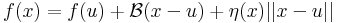
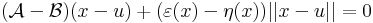
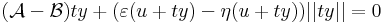
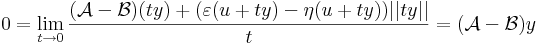
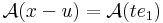
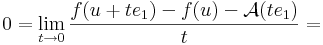
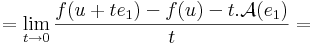
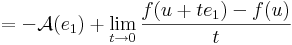
![[\mathrm{d}f(u)]=\mathbf{J}^f(u)=\begin{bmatrix}
\partial_1 f_1(u) & \partial_2 f_1(u) & \dots & \partial_n f_1(u)\\
\partial_1 f_2(u) & \partial_2 f_2(u) & \dots & \partial_n f_2(u)\\
\vdots & \vdots & \ddots & \vdots \\
\partial_1 f_m(u) & \partial_2 f_m(u) & \dots & \partial_n f_m(u)\\
\end{bmatrix}](/upload/math/b/c/8/bc8c1cf3c3d6f5032a7858552cc82a3a.png)