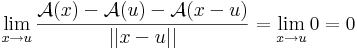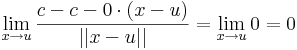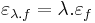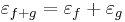Matematika A2a 2008/5. gyakorlat
Mozo (vitalap | szerkesztései) a (→Lineáris és affin függvény deriváltja) |
Mozo (vitalap | szerkesztései) (→A differenciálás tulajdonságai) |
||
| 17. sor: | 17. sor: | ||
===Függvények lineáris kombinációja=== | ===Függvények lineáris kombinációja=== | ||
| + | Ha ''f'' és ''g'' a ''H'' ⊆ '''R'''<sup>n</sup> halmazon értelmezett '''R'''<sup>m</sup>-be képező, az ''u'' ∈ ''H''-ban differenciálható függvények, akkor minden λ számra | ||
| + | :<math>\lambda.f\,</math> is differenciálható ''u''-ban és <math>\mathrm{d}(\lambda.f)(u)=\lambda.\mathrm{d}f(u)\,</math> és | ||
| + | :<math>f+g\,</math> is differenciálható ''u''-ban és <math>\mathrm{d}(f+g)(u)=\mathrm{d}f(u)+\mathrm{d}g(u)\,</math> | ||
| + | ''Ugyanis,'' a mondott differenciálokkal és a | ||
| + | :<math>\varepsilon_{\lambda.f}=\lambda.\varepsilon_{f}\,</math> | ||
| + | :<math>\varepsilon_{f+g}=\varepsilon_{f}+\varepsilon_{g}\,</math> | ||
| + | választással, ezek az ''u''-ban folytonosak lesznek és a lineáris résszekel együtt ezek előállítják a skalárszoros és összegfüggvények megváltozásait. | ||
| + | |||
| + | |||
A lap 2008. március 15., 13:31-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
A differenciálás tulajdonságai
Lineáris és affin függvény deriváltja
Az A : Rn  Rm lineáris leképezés differenciálható és differenciálja minden pontban saját maga.
Rm lineáris leképezés differenciálható és differenciálja minden pontban saját maga.
Ugyanis, legyen u ∈ Rn. Ekkor
c konstans függény esetén az dc(u)  0 alkalmas differenciálnak, mert
0 alkalmas differenciálnak, mert
így világos, hogy c + A alakú affin függvények is differenciálhatóak, és differenciáljuk minden pontban az az A lineáris leképezés, melynek eltolásából az affin származik. Ezt szintén behelyettesítéssel ellenőrizhetjük.
Tehát minden u ∈ Rn-re
Függvények lineáris kombinációja
Ha f és g a H ⊆ Rn halmazon értelmezett Rm-be képező, az u ∈ H-ban differenciálható függvények, akkor minden λ számra
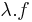 is differenciálható u-ban és
is differenciálható u-ban és 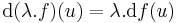 és
és
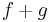 is differenciálható u-ban és
is differenciálható u-ban és 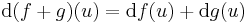
Ugyanis, a mondott differenciálokkal és a
választással, ezek az u-ban folytonosak lesznek és a lineáris résszekel együtt ezek előállítják a skalárszoros és összegfüggvények megváltozásait.
| 4. gyakorlat | 6. gyakorlat |