Matematika A2a 2008/5. gyakorlat
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Tartalomjegyzék |
A differenciálás tulajdonságai
Lineáris és affin függvény deriváltja
Az A : Rn  Rm lineáris leképezés differenciálható és differenciálja minden pontban saját maga.
Rm lineáris leképezés differenciálható és differenciálja minden pontban saját maga.
Ugyanis, legyen u ∈ Rn. Ekkor
c konstans függény esetén az dc(u)  0 alkalmas differenciálnak, mert
0 alkalmas differenciálnak, mert
így világos, hogy c + A alakú affin függvények is differenciálhatóak, és differenciáljuk minden pontban az az A lineáris leképezés, melynek eltolásából az affin származik. Ezt szintén behelyettesítéssel ellenőrizhetjük.
Tehát minden u ∈ Rn-re
Példa.
Az A: x  2x1 + 3x2 - 4x3 lineáris leképezés differenciálja az u pontban az u-tól független
2x1 + 3x2 - 4x3 lineáris leképezés differenciálja az u pontban az u-tól független
és Jacobi-mátrixa a konstans
mátrix.
Világos, hogy a
koordináta vagy projekciófüggvény lineáris, differenciálja minden u pontban saját maga és ennek mátrixa:
ahol az 1 az i-edik helyen áll. Másként
ahol
azaz a Kronecker-féle δ szimbólum.
Függvények lineáris kombinációja
Ha f és g a H ⊆ Rn halmazon értelmezett Rm-be képező, az u ∈ H-ban differenciálható függvények, akkor minden λ számra
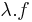 is differenciálható u-ban és
is differenciálható u-ban és 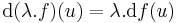 és
és
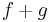 is differenciálható u-ban és
is differenciálható u-ban és 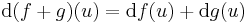
Ugyanis, a mondott differenciálokkal és a
választással, ezek az u-ban folytonosak lesznek és a lineáris résszekel együtt ezek előállítják a skalárszoros és összegfüggvények megváltozásait.
Függvénykompozíció differenciálja
Tétel. Legyen g: Rn ⊃ Rm, az u-ban differenciálható, f: Rm ⊃
Rm, az u-ban differenciálható, f: Rm ⊃ Rk a g(u)-ban differenciálható függvény, u ∈ int Dom(f
Rk a g(u)-ban differenciálható függvény, u ∈ int Dom(f 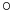 g). Ekkor az
g). Ekkor az
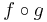 differenciálható u-ban és
differenciálható u-ban és
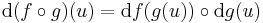
Bizonyítás. Alkalmas ε, A és η B párral, minden x ∈ Dom(f 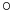 g)-re:
g)-re:
Innen leolvasható a differenciál és a másodrendben eltűnő mennyiség vektortényezője, az
melyben az első tag a 0-hoz tart, mivel a lineáris leképezés a 0-ban folytonos, és η a 0-hoz tart az u-ban. A második tag nulla szor korlátos alakú, hiszen a lineáris leképezés Lipschitz-tuladonsága folytán B minden egységvektoron korlátos értéket vesz fel.
Példa.
Mivel a gyökfüggvény nem differenciálható a 0-ban, ezért a differenciál csak nemnulla r-re számítható ki:
illetve a gradiens:
Szemléleti okokból lényeges, hogy itt . a skalárral való szorzás,  a skaláris szorzás.
a skaláris szorzás.
illetve a gradiens:
Szorzatok differenciálja
Most csak a sokféle szorzat deriváltjának értékét számítjuk ki. Minden esetben igazolható, hogy ha a formulákban szereplő összes derivált létezik, akkor a formula érvényes (sőt, ha a függvények az adott pontban differenciálhatók, akkor a szorzat is differenciálható az adott pontban). Az mátrixelemeket indexesen számítjuk.
Skalárok szorzata
λ, μ: H  R, ahol H ⊆ Rn és az u ∈ H-ban mindketten differenciálhatók, akkor λμ is és
R, ahol H ⊆ Rn és az u ∈ H-ban mindketten differenciálhatók, akkor λμ is és
Skalárral való szorzás
| 4. gyakorlat | 6. gyakorlat |
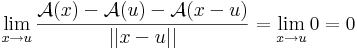
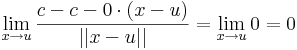

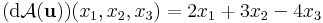
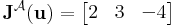
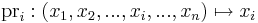
![[\mathrm{grad}\,\mathrm{pr_i}]=\mathbf{J}^{\mathrm{pr}_i}(\mathbf{u})=\begin{bmatrix}0 & 0 & ... & 1 & ...& 0\end{bmatrix}](/upload/math/f/a/5/fa51c1bb60d1e414a5acb5c8e93ae7d2.png)
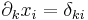
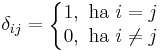
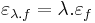
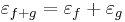
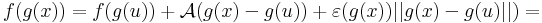
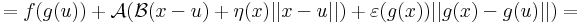
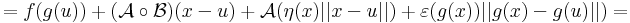
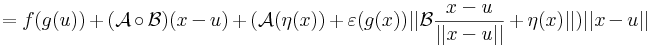
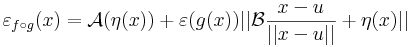
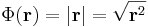
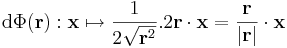
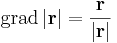
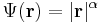
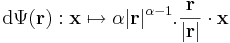
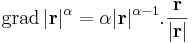
![[\mathrm{d}(\lambda\mu)(u)]_{1j}=\partial_j(\lambda\mu)=\mu\partial_j\lambda+\lambda\partial_j\mu=[\mu(u).\mathrm{grad}\,\lambda(u)+\lambda(u).\mathrm{grad}\,\mu(u)]_{1j}](/upload/math/7/2/8/728e17dabcb211df47d969b4438913c1.png)