Matematika A2a 2008/6. gyakorlat
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) |
||
| (egy szerkesztő egy közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
:''Ez az szócikk a [[Matematika A2a 2008]] alszócikke.'' | :''Ez az szócikk a [[Matematika A2a 2008]] alszócikke.'' | ||
| + | ==Szélsőérték szükséges feltétele== | ||
| + | |||
| + | Egyelőre állapodjunk meg abban, hogy gradiensnek nevezzük a következő többváltozós vektorértékű függvényt: ha ''f'': '''R'''<sup>n</sup> <math>\supset\!\to</math> '''R''' parciálisan differenciálható, akkor | ||
| + | :<math>\mathrm{grad}\,f(x)=(\partial_1f(x),...,\partial_nf(x))</math> | ||
| + | mely lényegében az ''f'' elsőrendű parciális deriváltjaiból képezett vektor. | ||
| + | |||
| + | Később a gradienst egy kissé másképp fogjuk értelmezni és amit most definiáltunk, az a gradiens sztenderd bázisbeli mátrixa lesz (adott pontra vonatkozóan). | ||
| + | |||
| + | |||
| + | '''Tétel''' - ''Fermat-tétel'' - Legyen ''f'': '''R'''<sup>n</sup> <math>\supset\!\to</math> '''R''', ''u'' ∈ int Dom(''f''), ''f'' parciálisan differenciálható ''u''-ban. | ||
| + | :Ha ''u''-ban ''f''-nek (lokális) szélsőértéke van, akkor | ||
| + | ::<math>\mathrm{grad}\,f(u)=0_{\mathbf{R}^n}\,</math> | ||
| + | ''U.is:'' minden ''i''-re az ''i''-edik parciális függvénynek szélsőértéke van ''u''<sub>i</sub>-ben, így az egyváltozós Fermat-tétel miatt ezeknek a deriváltja ''u''<sub>i</sub>-ben 0, így a gradiens értéke 0. | ||
| + | |||
| + | ====Példa==== | ||
| + | :<math>f(x,y)=x^2y^2\,</math> | ||
| + | Ennek gradiense: | ||
| + | :<math>\mathrm{grad}\,f(x,y)=(2xy^2,2yx^2)</math> | ||
| + | Az | ||
| + | :<math>\left. | ||
| + | \begin{matrix} | ||
| + | \mathrm{I.} & 2xy^2 & = & 0\\ | ||
| + | \mathrm{II.} & 2yx^2 & = & 0\\ | ||
| + | \end{matrix} | ||
| + | \right\}</math> | ||
| + | egyenletrendszer megoldásai: ''x'' = 0, ''y'' tetszőleges ill. ''y'' = 0 és ''x'' tetszőleges. A szélsőértékek helyei csak ezek közül kerülhetnek ki és ezek valóban szélsőértékek is, mert ezeken a függvény 0-t vesz fel, ami a lehetséges legkisebb értéke. | ||
| + | :<gnuplot> | ||
| + | set pm3d | ||
| + | set size 0.8,0.8 | ||
| + | set xrange [-1:1] | ||
| + | set yrange [-1:1] | ||
| + | set zrange [-2:2] | ||
| + | set view 50,30,1,1 | ||
| + | unset xtics | ||
| + | unset ytics | ||
| + | unset ztics | ||
| + | unset key | ||
| + | unset colorbox | ||
| + | splot 5*x*x*y*y | ||
| + | </gnuplot> | ||
| + | |||
| + | ==Magasabbrendű parciális deriváltak== | ||
| + | Ha ''f'' parciálisan deriválható, akkor ∂<sub>1</sub>''f'' és ∂<sub>2</sub>''f'' szintén kétváltozós függvények (a pontonként a deriváltak, mint függvényértékek értelmezésével) és érdeklődhetünk ezek parciális differenciálhatóságuk iránt. Például: | ||
| + | |||
| + | :<math>f(x,y)=x^2y^4+x^5-y^3\,</math> | ||
| + | |||
| + | :<math>\partial_xf(x,y)=xy^4+5x^4</math> | ||
| + | :<math>\partial_yf(x,y)=x^24y^3-3y^2</math> | ||
| + | |||
| + | :<math>\partial_x(\partial_xf)(x,y)=y^4+20x^3</math> | ||
| + | :<math>\partial_y(\partial_yf)(x,y)=12x^2y^2-6y^2</math> | ||
| + | :<math>\partial_y(\partial_xf)(x,y)=x4y^3</math> | ||
| + | :<math>\partial_x(\partial_yf)(x,y)=4xy^3</math> | ||
| + | |||
| + | És valóban: | ||
| + | |||
| + | '''Tétel.''' (Young-tétel) Ha a másodrendű parciláis deriváltak léteznek az ''u'' egy környezetében és folytonosak az ''u'' pontban, akkor az ''u''-beli vegyes másodrendű parciláis deriváltak egyenlőek: | ||
| + | :<math>\partial_x(\partial_y f)(u)=\partial_y(\partial_x f)(u)</math> | ||
| + | |||
| + | Azaz az alábbi, úgy nevezett Hesse-mátrix szimmetrikus: | ||
| + | :<math>H^f(u)=\begin{bmatrix} | ||
| + | \cfrac{\partial^2 f(u)}{\partial x^2} & \cfrac{\partial^2 f(u)}{\partial y\partial x}\\\\ | ||
| + | \cfrac{\partial^2 f(u)}{\partial x\partial y} & \cfrac{\partial^2 f(u)}{\partial y^2} | ||
| + | \end{bmatrix}</math> | ||
| + | |||
| + | '''Feladat.''' Az a kitétel, hogy az ''u''-ban a másodrenrű parciláis deriváltak folytonosak, nem hagyható el, ugyanis. Legyen | ||
| + | :<math>f(x,y)=\left\{\begin{matrix} | ||
| + | 0,& \mbox{ ha }(x,y)=(0,0)\\ | ||
| + | \frac{xy(x^2-y^2)}{x^2+y^2},& \mbox{ ha }(x,y)\ne(0,0) | ||
| + | \end{matrix}\right.</math> | ||
| + | Ekkor a 0-ban nem egyenlő a két vegyes parciális derivált. | ||
| + | |||
| + | Tekintsük a parciális deriváltakat: | ||
| + | :<math>\partial_x(\partial_yf)(0,0)=\lim\limits_{x\to 0}\frac{(\partial_yf)(x,0)-(\partial_yf)(0,0)}{x}</math> | ||
| + | :<math>\partial_y(\partial_xf)(0,0)=\lim\limits_{y\to 0}\frac{(\partial_xf)(0,y)-(\partial_xf)(0,0)}{y}</math> | ||
| + | :<math>\partial_x(\partial_xf)(0,0)=\lim\limits_{x\to 0}\frac{(\partial_xf)(x,0)-(\partial_xf)(0,0)}{x}</math> | ||
| + | :<math>\partial_y(\partial_yf)(0,0)=\lim\limits_{y\to 0}\frac{(\partial_yf)(0,y)-(\partial_yf)(0,0)}{y}</math> | ||
| + | Ehhez tehát elegendő kiszámítani a következő föggvényeket: y <math>\mapsto</math> (∂<sub>x</sub>f)(0,y), x <math>\mapsto</math> (∂<sub>y</sub>f)(x,0). Ehhez a parciális deriváltak: | ||
| + | :<math>\partial_xf(0,y)=\lim\limits_{t\to 0}\frac{f(t,y)-f(0,0)}{t}=\left\{\begin{matrix} | ||
| + | 0,& \mbox{ ha }y=0\\ | ||
| + | -y,& \mbox{ ha }y\ne 0 | ||
| + | \end{matrix}\right.</math> | ||
| + | :<math>\partial_yf(x,0)=\lim\limits_{t\to 0}\frac{f(x,t)-f(0,0)}{t}=\left\{\begin{matrix} | ||
| + | 0,& \mbox{ ha }x=0\\ | ||
| + | x,& \mbox{ ha }x\ne 0 | ||
| + | \end{matrix}\right.</math> | ||
| + | :<math>\partial_yf(0,y)=\lim\limits_{t\to 0}\frac{f(0,y+t)-f(0,0)}{t}=0</math> | ||
| + | :<math>\partial_xf(x,0)=\lim\limits_{t\to 0}\frac{f(x+t,0)-f(0,0)}{t}=0</math> | ||
| + | |||
| + | Megjegyezzük, hogy a g=(∂<sub>x</sub>f,∂<sub>y</sub>f) függvény (0,0)-beli parciális deriváltjai nem lehetnek folytonosak, mert ott a függvény nem totálisan diffható. Ugyanis a g Jacobi-mátrixa: | ||
| + | :<math>J^g(0,0)=H^f(0,0)=\begin{bmatrix} | ||
| + | 0 & -1\\ | ||
| + | 1 & 0 | ||
| + | \end{bmatrix}</math> | ||
| + | ami a 90˚-os forgatás. Ekkor a g-t a (t,0) vektorral közelítve a 0-ba: | ||
| + | :<math>\lim\limits_{t\to 0}\frac{g(t,0)-g(0,0)-J^g(0,0)\cdot (t,0)}{|t|}=\lim\limits_{t\to 0}\frac{(0,-t)}{|t|}\ne (0,0)\,</math> | ||
| + | márpedig ha g minden parciális deriváltja folytonos lenne a (0,0)-ban, akkor g totálisan is deriválható lenne. | ||
| + | |||
| + | ==Többváltozós függvény szélsőértéke== | ||
| + | |||
| + | |||
| + | ===Másodikderivált próba=== | ||
| + | Kétszer differenciálható függvényre vonatkozóan megfogalmazhatjuk a lokális maximum és minimum létezésének elégséges feltételét. Csak a kétváltozós függvényekkel foglalkozunk. Tegyük fel, hogy grad ''f''(u) = 0 és H<sup>f</sup>(u) az ''f'' Hesse-mátrixa | ||
| + | # ha det H<sup>f</sup>(u) > 0 és ∂<sub>11</sub>''f''(''u'') < 0, akkor ''f''-nek ''u''-ban '''maximuma''' van | ||
| + | # ha det H<sup>f</sup>(u) > 0 és ∂<sub>11</sub>''f''(''u'') > 0, akkor ''f''-nek ''u''-ban '''minimuma''' van | ||
| + | # ha det H<sup>f</sup>(u) < 0, akkor ''f''-nek biztosan nincs szélsőértéke, ún. '''nyeregpont'''ja van | ||
| + | # ha det H<sup>f</sup>(u) = 0, akkor a próba nem járt sikerrel, azaz további vizsgálatokat igényel annak eldöntése, hogy ''u'' szélsőérték hely-e. | ||
| + | |||
| + | ''Megjegyzések.'' Mivel kétváltozós esetben | ||
| + | :<math>\mathrm{det}\,\mathrm{H}^f(u)=\partial_{11}f(u)\cdot \partial_{22}f(u)-(\partial_{12}f(u))^2</math> | ||
| + | ezért olyan eset nem létezik, hogy det H<sup>f</sup>(u) > 0 és ∂<sub>11</sub>''f''(''u'') = 0. | ||
| + | |||
| + | Világos, hogy a másodikderivált tipikusan azoknál a függvényeknél jár sikerrel, melyeket egy másodfokú függvény közelít a legjobban (aszimptotikusan másodfokúak). Ha a függvény ennél magasabb fokú, akkor a második deriváltak eltűnnek és a Hesse-mártix elfajul (vagy legalább is tipikusan elfajul). | ||
| + | |||
| + | Ha tehát | ||
| + | :<math>\mathrm{H}^{f}(u)=\begin{pmatrix} | ||
| + | A & B \\ | ||
| + | B & C | ||
| + | \end{pmatrix}</math>, akkor <math>\mathrm{det\,H}^{f}(u)=AC - B^2 </math>, | ||
| + | és így a tipikus példák a következők. | ||
| + | |||
| + | ====Példák==== | ||
| + | |||
| + | '''1.''' Ha B kicsi, azaz az AC-hez képest kis abszolútrétékű szám, akkor a szélsőérték irányába mozdul el a feladat. | ||
| + | :<math>f(x,y)=x^2+xy+y^2\,</math> | ||
| + | |||
| + | Ekkor grad ''f'' = ( 2x + y , 2y + x ) és | ||
| + | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix} | ||
| + | 2 & 1 \\ | ||
| + | 1 & 2 | ||
| + | \end{pmatrix}</math> | ||
| + | azaz 4 - 1 = 3 > 0 és 2 > 0 miatt minimum. | ||
| + | :<gnuplot> | ||
| + | set pm3d | ||
| + | set size 0.8,0.8 | ||
| + | set xrange [-1:1] | ||
| + | set yrange [-1:1] | ||
| + | set zrange [-2:2] | ||
| + | set view 50,30,1,1 | ||
| + | unset xtics | ||
| + | unset ytics | ||
| + | unset ztics | ||
| + | unset key | ||
| + | unset colorbox | ||
| + | splot x*x+x*y+y*y | ||
| + | </gnuplot> | ||
| + | |||
| + | '''2.''' Ha |B| nagy (azaz AC-hez képest nagy), akkor a bizonyosan nemszélsőérték irányába. | ||
| + | :<math>f(x,y)=x^2-3xy+y^2\,</math> | ||
| + | |||
| + | Ekkor grad ''f'' = ( 2x + -3y , 2y + -3x ) és | ||
| + | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix} | ||
| + | 2 & -3 \\ | ||
| + | -3 & 2 | ||
| + | \end{pmatrix}</math> | ||
| + | azaz 4 - 9 = -5 < 0 miatt nincs szélsőérték: nyeregpont. | ||
| + | :<gnuplot> | ||
| + | set pm3d | ||
| + | set size 0.8,0.8 | ||
| + | set xrange [-1:1] | ||
| + | set yrange [-1:1] | ||
| + | set zrange [-2:2] | ||
| + | set view 50,30,1,1 | ||
| + | unset xtics | ||
| + | unset ytics | ||
| + | unset ztics | ||
| + | unset key | ||
| + | unset colorbox | ||
| + | splot x*x -3*x*y+y*y | ||
| + | </gnuplot> | ||
| + | |||
| + | '''3.''' Negatív A és C-re és kis B-re: | ||
| + | :<math>f(x,y)=-x^2+xy-y^2\,</math> | ||
| + | |||
| + | Ekkor grad ''f'' = ( -2x + 3y , -2y + 3x ) és | ||
| + | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix} | ||
| + | -2 & 1 \\ | ||
| + | 1 & -2 | ||
| + | \end{pmatrix}</math> | ||
| + | azaz 4 - 1 = 3 > 0 és -2 < 0 miatt maximum. | ||
| + | :<gnuplot> | ||
| + | set pm3d | ||
| + | set size 0.8,0.8 | ||
| + | set xrange [-1:1] | ||
| + | set yrange [-1:1] | ||
| + | set zrange [-2:2] | ||
| + | set view 50,30,1,1 | ||
| + | unset xtics | ||
| + | unset ytics | ||
| + | unset ztics | ||
| + | unset key | ||
| + | unset colorbox | ||
| + | splot -x*x +x*y-y*y | ||
| + | </gnuplot> | ||
| + | |||
| + | '''4.''' Ha A és C előjele ellenkező, akkor rögtön következik, hogy nincs sz.é. | ||
| + | :<math>f(x,y)=x^2+xy-y^2\,</math> | ||
| + | |||
| + | Ekkor grad ''f'' = ( 2x + y , -2y + x ) és | ||
| + | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix} | ||
| + | 2 & 1 \\ | ||
| + | 1 & -2 | ||
| + | \end{pmatrix}</math> | ||
| + | azaz -4 - 1 = -5 < 0 azaz nyeregpont. | ||
| + | :<gnuplot> | ||
| + | set pm3d | ||
| + | set size 0.8,0.8 | ||
| + | set xrange [-1:1] | ||
| + | set yrange [-1:1] | ||
| + | set zrange [-2:2] | ||
| + | set view 50,30,1,1 | ||
| + | unset xtics | ||
| + | unset ytics | ||
| + | unset ztics | ||
| + | unset key | ||
| + | unset colorbox | ||
| + | splot x*x +x*y-y*y | ||
| + | </gnuplot> | ||
| + | |||
| + | '''5.''' Atipikus eset, ha AC = B<sup>2</sup>. Ekkor nem jár sikerrel a próba: | ||
| + | :<math>f(x,y)=x^2+2xy+y^2\,</math> | ||
| + | |||
| + | Ekkor grad ''f'' = ( 2x + 2y , 2y + 2x ) és | ||
| + | :<math>\mathrm{H}^{f}(x,y)=\begin{pmatrix} | ||
| + | 2 & 2 \\ | ||
| + | 2 & 2 | ||
| + | \end{pmatrix}</math> | ||
| + | azaz 4 - 4 = 0, azaz határozatlan eset. | ||
| + | De tudjuk, hogy | ||
| + | :<math>f(x,y)=(x+y)^2\,</math> | ||
| + | ami pontosan akkor minimális, ha x = -y, azaz ezeken a helyeken van szélsőérték. | ||
| + | :<gnuplot> | ||
| + | set pm3d | ||
| + | set size 0.8,0.8 | ||
| + | set xrange [-1:1] | ||
| + | set yrange [-1:1] | ||
| + | set zrange [-2:2] | ||
| + | set view 50,30,1,1 | ||
| + | unset xtics | ||
| + | unset ytics | ||
| + | unset ztics | ||
| + | unset key | ||
| + | unset colorbox | ||
| + | splot (x+y)*(x+y) | ||
| + | </gnuplot> | ||
A lap jelenlegi, 2017. február 19., 19:26-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Tartalomjegyzék |
Szélsőérték szükséges feltétele
Egyelőre állapodjunk meg abban, hogy gradiensnek nevezzük a következő többváltozós vektorértékű függvényt: ha f: Rn 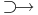 R parciálisan differenciálható, akkor
R parciálisan differenciálható, akkor
mely lényegében az f elsőrendű parciális deriváltjaiból képezett vektor.
Később a gradienst egy kissé másképp fogjuk értelmezni és amit most definiáltunk, az a gradiens sztenderd bázisbeli mátrixa lesz (adott pontra vonatkozóan).
Tétel - Fermat-tétel - Legyen f: Rn 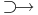 R, u ∈ int Dom(f), f parciálisan differenciálható u-ban.
R, u ∈ int Dom(f), f parciálisan differenciálható u-ban.
- Ha u-ban f-nek (lokális) szélsőértéke van, akkor
U.is: minden i-re az i-edik parciális függvénynek szélsőértéke van ui-ben, így az egyváltozós Fermat-tétel miatt ezeknek a deriváltja ui-ben 0, így a gradiens értéke 0.
Példa
Ennek gradiense:
Az
egyenletrendszer megoldásai: x = 0, y tetszőleges ill. y = 0 és x tetszőleges. A szélsőértékek helyei csak ezek közül kerülhetnek ki és ezek valóban szélsőértékek is, mert ezeken a függvény 0-t vesz fel, ami a lehetséges legkisebb értéke.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot 5*x*x*y*y
Magasabbrendű parciális deriváltak
Ha f parciálisan deriválható, akkor ∂1f és ∂2f szintén kétváltozós függvények (a pontonként a deriváltak, mint függvényértékek értelmezésével) és érdeklődhetünk ezek parciális differenciálhatóságuk iránt. Például:
És valóban:
Tétel. (Young-tétel) Ha a másodrendű parciláis deriváltak léteznek az u egy környezetében és folytonosak az u pontban, akkor az u-beli vegyes másodrendű parciláis deriváltak egyenlőek:
Azaz az alábbi, úgy nevezett Hesse-mátrix szimmetrikus:
Feladat. Az a kitétel, hogy az u-ban a másodrenrű parciláis deriváltak folytonosak, nem hagyható el, ugyanis. Legyen
Ekkor a 0-ban nem egyenlő a két vegyes parciális derivált.
Tekintsük a parciális deriváltakat:
Ehhez tehát elegendő kiszámítani a következő föggvényeket: y  (∂xf)(0,y), x
(∂xf)(0,y), x  (∂yf)(x,0). Ehhez a parciális deriváltak:
(∂yf)(x,0). Ehhez a parciális deriváltak:
Megjegyezzük, hogy a g=(∂xf,∂yf) függvény (0,0)-beli parciális deriváltjai nem lehetnek folytonosak, mert ott a függvény nem totálisan diffható. Ugyanis a g Jacobi-mátrixa:
ami a 90˚-os forgatás. Ekkor a g-t a (t,0) vektorral közelítve a 0-ba:
márpedig ha g minden parciális deriváltja folytonos lenne a (0,0)-ban, akkor g totálisan is deriválható lenne.
Többváltozós függvény szélsőértéke
Másodikderivált próba
Kétszer differenciálható függvényre vonatkozóan megfogalmazhatjuk a lokális maximum és minimum létezésének elégséges feltételét. Csak a kétváltozós függvényekkel foglalkozunk. Tegyük fel, hogy grad f(u) = 0 és Hf(u) az f Hesse-mátrixa
- ha det Hf(u) > 0 és ∂11f(u) < 0, akkor f-nek u-ban maximuma van
- ha det Hf(u) > 0 és ∂11f(u) > 0, akkor f-nek u-ban minimuma van
- ha det Hf(u) < 0, akkor f-nek biztosan nincs szélsőértéke, ún. nyeregpontja van
- ha det Hf(u) = 0, akkor a próba nem járt sikerrel, azaz további vizsgálatokat igényel annak eldöntése, hogy u szélsőérték hely-e.
Megjegyzések. Mivel kétváltozós esetben
ezért olyan eset nem létezik, hogy det Hf(u) > 0 és ∂11f(u) = 0.
Világos, hogy a másodikderivált tipikusan azoknál a függvényeknél jár sikerrel, melyeket egy másodfokú függvény közelít a legjobban (aszimptotikusan másodfokúak). Ha a függvény ennél magasabb fokú, akkor a második deriváltak eltűnnek és a Hesse-mártix elfajul (vagy legalább is tipikusan elfajul).
Ha tehát
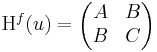 , akkor
, akkor 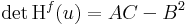 ,
,
és így a tipikus példák a következők.
Példák
1. Ha B kicsi, azaz az AC-hez képest kis abszolútrétékű szám, akkor a szélsőérték irányába mozdul el a feladat.
Ekkor grad f = ( 2x + y , 2y + x ) és
azaz 4 - 1 = 3 > 0 és 2 > 0 miatt minimum.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot x*x+x*y+y*y
2. Ha |B| nagy (azaz AC-hez képest nagy), akkor a bizonyosan nemszélsőérték irányába.
Ekkor grad f = ( 2x + -3y , 2y + -3x ) és
azaz 4 - 9 = -5 < 0 miatt nincs szélsőérték: nyeregpont.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot x*x -3*x*y+y*y
3. Negatív A és C-re és kis B-re:
Ekkor grad f = ( -2x + 3y , -2y + 3x ) és
azaz 4 - 1 = 3 > 0 és -2 < 0 miatt maximum.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot -x*x +x*y-y*y
4. Ha A és C előjele ellenkező, akkor rögtön következik, hogy nincs sz.é.
Ekkor grad f = ( 2x + y , -2y + x ) és
azaz -4 - 1 = -5 < 0 azaz nyeregpont.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot x*x +x*y-y*y
5. Atipikus eset, ha AC = B2. Ekkor nem jár sikerrel a próba:
Ekkor grad f = ( 2x + 2y , 2y + 2x ) és
azaz 4 - 4 = 0, azaz határozatlan eset. De tudjuk, hogy
ami pontosan akkor minimális, ha x = -y, azaz ezeken a helyeken van szélsőérték.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot (x+y)*(x+y)
Kiegészítés
Skalárfüggvények szorzata
λ, μ: H  R, ahol H ⊆ Rn és az u ∈ H-ban mindketten differenciálhatók, akkor λμ is és
R, ahol H ⊆ Rn és az u ∈ H-ban mindketten differenciálhatók, akkor λμ is és
azaz
Példa
Számoljuk ki r2 deriváltját a szorzat szabálya szerint.
Egyrészt, ha r ≠ 0, akkor
Másrészt, ha r = 0, akkor
minden r-re fennáll, így grad(id2)(0) = 0 alkalmas az ε(r)=|r|-rel, tehát r2 differenciálható 0-ban is.
a × ... operátor
Differenciálható-e és ha igen mi a differenciálja, divergenciája, rotációja a
leképezésnek, ahol a előre megadott konstans vektor.
Megoldás
Az a × ..., azaz az
(itt I az identitás leképezés) leképezés lineáris, minthogy a vektoriális szorzás mindkét változójában lineáris (v ∈ Lin(R3;R3)), így differenciálható és differenciálja saját maga:
azaz
minden h és r ∈ R3 vektorra.
Jacobi-mátrixa (a sztenderd bázisbeli mátrixa) tetszőleges (x,y,z) pontban:
Mivel a főátlóbeli elemek mind nullák, ezért ebből rögtön következik, hogy div(a × I)(r) = 0.
azaz rot v (r) = 2a. Az előbb felhasználtuk a kettős vektoriális szorzatra vonatkozó kifejtési tétel indexes alakját, a
ami azt mondja, hogy ha az ijk és klm-ben a nem azonos párok jó sorrendben következnek, akkor az epszolon 1-et, ha rossz sorrendben, akkor -1-et ad.
a  ... operátor
... operátor
Differenciálható-e és ha igen mi a differenciálja
leképezésnek, ahol a előre megadott konstans vektor.
Megoldás
Skalártér lévén Φ gradiensét kell kiszámolnunk. Mivel ez is lineáris leképezés, ezért differenciálható és differenciálja saját maga, azaz a gradiens vektor pont a:
Ezt persze indexes deriválással is kiszámítható:
További példa skalárfüggvényre
Hatérozzuk meg a Φ
(ahol i az x irányú egységvektor, |.| a vektor hossza) függvény szintvonalait, differenciálhatóságát, gradiensét!
Megoldás
Érdemes koordinátás írásmódra áttérni, hiszen az i vektor úgy is a koordinátarendszerhez kapcsolódik. A vektoriális szorzás definíciója miatt
Tehát azok a pontok vannak azonos szintfelületen, melyeknek az [yz] síkra vett vetületük azonos hosszúságú (i × r hossza az i-re merőleges komponense r-nek). Az
- y2 + z2 = 0
egyenlettel megadott pontokban (másként: y = 0 & z = 0 & x tetszőleges) a függvény nem differenciálható, ugyanis a Φ=0 szintfelület elfajúlt módon csak egy egyenes, az x tengely, így a gradiens vektor iránya nem egyértelmű. Ezt azzal is igazolhatjuk, ha vesszük ezekben a pontokban például az y irányú parciális függvényt:
azaz az (x0,0,0) pontokhoz tartozó Φ(x0, . ,0) parciális függvény nem differenciálható a 0-ban.
Máshol a gradiensvektor, a parciális deriváltakat kiszámítva
vagy másként:
Megjegyezzük, hogy ehhez még a függvénykompozíció deriválási szabályával is lejuthattunk volna:
Indexes deriválás
Most csak a sokféle szorzat deriváltjának értékét számítjuk ki. Minden esetben igazolható, hogy ha a formulákban szereplő összes derivált létezik, akkor a formula érvényes (sőt, ha a függvények az adott pontban differenciálhatók, akkor a szorzat is differenciálható az adott pontban). Az mátrixelemeket indexesen számítjuk.
Feltéve például, hogy az f többváltozós skalárfüggvény parciálisan differenciálható, a gradiens elemeit így nyerjük:
1. Példa
Ha f(r) = r2, akkor
de a koordinátafüggvények deriváltjairól tudjuk, hogy azoknak az értékét a Kronecker-delta adja:
azaz
tehát parciálisan differenciálható minden pontban és a Jacobi-mártix elemei a fentiek.
2. Példa
Ha f(r) = ar, akkor
3. Példa
Ha f(r) = |r|α, akkor
itt ne feledjük, hogy k-ra szummázunk és hogy az összetett tényezőben a skaláris szorzat szerepel:
tehát parciálisan differenciálható minden pontban és a Jacobi-mártix elemei a fentiek.
Deriválttenzor és invariánsai
Ha A az f:Rn ⊃ Rn leképezés differenciálja az u pontban, akkor A-t deriválttenzornak nevezzük. Minden tenzor egyértelműen előáll egy szimmetrikus és egy antiszimmetrikus tenzor összegeként:
Rn leképezés differenciálja az u pontban, akkor A-t deriválttenzornak nevezzük. Minden tenzor egyértelműen előáll egy szimmetrikus és egy antiszimmetrikus tenzor összegeként:
Ebből a szimmetrikus rész főátlbeli elemeinek összege minden bázisban ugyanaz a skaláris érték, melyet a tenzor nyomának, illetve a függvény divergenciájának nevezzük:
 illetve
illetve 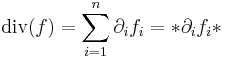
Az utóbbi írásmód a koordinátás alakban az úgy nevezett Einstein-féle jelölési konvenció, amelynek elve, hogy a kétszer stereplő indexekre automatikusan szumma értendő.
Példa
f:R3 ⊃ R3
esetben a tenzor antiszimmetrikus részéhez egyértelműen létezik egy olyan a vektor, hogy minden r-re:
R3
esetben a tenzor antiszimmetrikus részéhez egyértelműen létezik egy olyan a vektor, hogy minden r-re:
mely vektort az f rotációjának nevezzük:
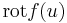 és
és ![[\mathrm{rot}f(u)]_i=\sum\limits_{j,k=1}^3\varepsilon_{ijk}\partial_j f_k=*\varepsilon_{ijk}\partial_j f_k*](/upload/math/b/e/d/bed2ac05c3c84c0a2da64ec31206b3fa.png)
ahol
a Levi-Civita-szimbólum.
Skalárfüggvénnyel való szorzás
λ: H  R, f:H
R, f:H  Rm, ahol H ⊆ Rn és az u ∈ H-ban mindketten differenciálhatók, akkor λ.f is és
Rm, ahol H ⊆ Rn és az u ∈ H-ban mindketten differenciálhatók, akkor λ.f is és
azaz
ahol 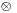 a diadikus szorzat, melynek koordinátamátrixa egy oszlopvektor (balról) és egy sorvektor (jobbról) mátrixszorzatából adódik. Ez ritkán kell teljes egészében, a két invariáns (rot-nál csak 3×3-as esetben) a gyakoribb.
a diadikus szorzat, melynek koordinátamátrixa egy oszlopvektor (balról) és egy sorvektor (jobbról) mátrixszorzatából adódik. Ez ritkán kell teljes egészében, a két invariáns (rot-nál csak 3×3-as esetben) a gyakoribb.
Vektorfüggvények skaláris szorzata
f,g:H  Rm, ahol H ⊆ Rn és az u ∈ H-ban mindketten differenciálhatók, akkor f
Rm, ahol H ⊆ Rn és az u ∈ H-ban mindketten differenciálhatók, akkor f g is és
g is és
azaz
illetve a Jacobi-mátrixszal:
ahol [.]T az oszlopvektor transzponáltját, 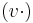 pedig a v vektorral történő skaláris szorzás operátorát jelöli.
pedig a v vektorral történő skaláris szorzás operátorát jelöli.
| 5. gyakorlat | 7. gyakorlat |
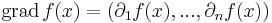
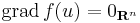
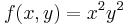
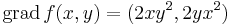
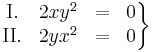
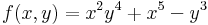
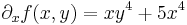
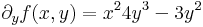
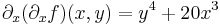
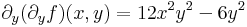
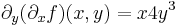
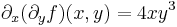
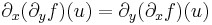
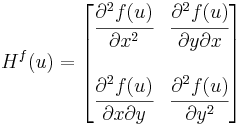
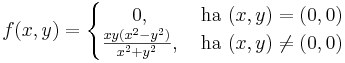
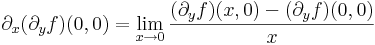
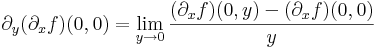
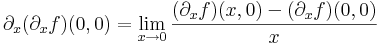
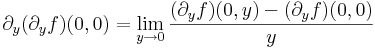
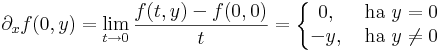
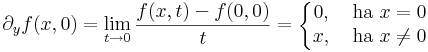
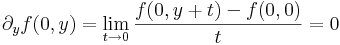
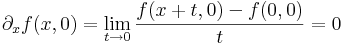
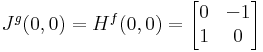
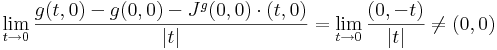
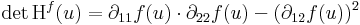
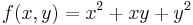
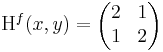
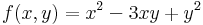
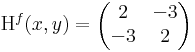
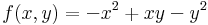
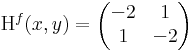
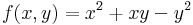
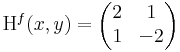
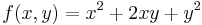
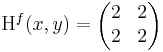
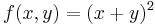
![[\mathrm{d}(\lambda\mu)(u)]_{1j}=\partial_j(\lambda\mu)=\mu\partial_j\lambda+\lambda\partial_j\mu=[\mu(u).\mathrm{grad}\,\lambda(u)+\lambda(u).\mathrm{grad}\,\mu(u)]_{j}](/upload/math/c/0/6/c06d0e7630e5abf100915f67de31ed5d.png)
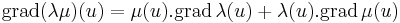
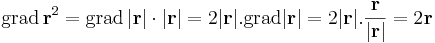
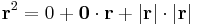
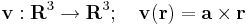
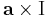
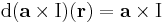
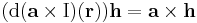
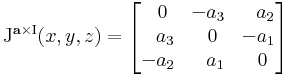
![[\mathrm{rot}\,\mathbf{v}]_i=\varepsilon_{ijk}\partial_j\varepsilon_{klm}a_lx_m=\varepsilon_{ijk}\varepsilon_{klm}a_l\partial_j x_m=\varepsilon_{ijk}\varepsilon_{klm}a_l\delta_{jm}=\varepsilon_{ijk}\varepsilon_{klj}a_l=](/upload/math/6/4/2/642b95a997703a68637ff5897331d591.png)
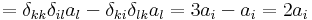
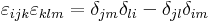
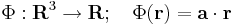
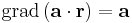
![[\mathrm{grad}\,\Phi]_i=\partial_ia_kx_k=a_k\partial_ix_k=a_k\delta_{ik}=a_i\,](/upload/math/e/6/7/e67c528d00633fe5efe34a67e9c2aef9.png)
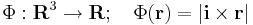
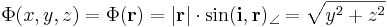
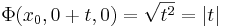
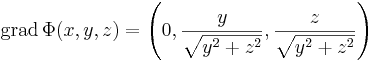
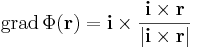
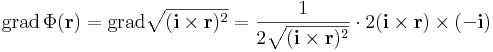
![[\mathrm{grad}\,f]_i=\partial_if\,](/upload/math/f/a/3/fa3c940fa1fad80ffb905f790caa7495.png)
![\mathbf{r}^2=\sum\limits_{k=1}^3 [\mathbf{r}]_k[\mathbf{r}]_k=\sum\limits_{k=1}^3 x_kx_k=[\mathrm{Einstein\;konv.}]\;x_kx_k](/upload/math/d/8/b/d8b7a2ddcfd984008eedaf9f2fc25505.png)
![[\mathrm{grad}\,f]_i=\partial_ix_kx_k\,=x_k\partial_ix_k+x_k\partial_ix_k\,](/upload/math/9/c/7/9c7478f0fc6c90cb7d94d0f617d8d49a.png)
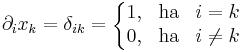
![[\mathrm{grad}\,f]_i=2x_k\delta_{ik}=2x_i=[2\mathbf{r}]_i\,](/upload/math/d/7/8/d784a387f1c950a3e0e038cc56a61cbd.png)
![[\mathrm{grad}\,f]_i=\partial_ia_kx_k\,=a_k\partial_ix_k=a_k\delta_{ik}\,=a_i=[\mathbf{a}]_i](/upload/math/a/5/7/a57f9bc5e37f361c19f92eee518f6f06.png)
![[\mathrm{grad}\,f]_i=\partial_i(x_kx_k)^{\alpha/2}\,=\partial_i(x_k)^{\alpha}=\frac{\alpha}{2}(x_kx_k)^{\frac{\alpha}{2}-1}2\delta_{ik}x_k\,](/upload/math/7/1/8/71892bcadec17b766681f84d469b9ff3.png)
![[\mathrm{grad}\,f]_i=\alpha(x_kx_k)^{\frac{\alpha}{2}-1}x_i\,=\left[\alpha|\mathbf{r}|^\alpha\frac{\mathbf{r}}{\mathbf{r}^2}\right]_i=\left[\alpha|\mathbf{r}|^{\alpha-1}\frac{\mathbf{r}}{|\mathbf{r}|}\right]_i](/upload/math/0/d/e/0ded0710fdc3c526de84bc11a3747b26.png)
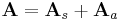
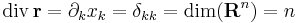
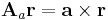
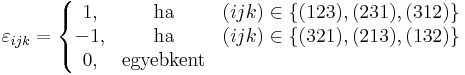
![[\mathrm{d}(\lambda.f)(u)]_{ij}=\partial_j(\lambda.f)=\partial_j\lambda f_i=f_i\partial_j\lambda+\lambda \partial_jf_i](/upload/math/3/f/f/3ff67b8cf3567d0fa54ce6ef1b76ee50.png)
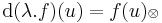
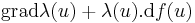
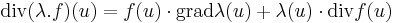
![[\mathrm{rot}(\lambda.f)(u)]_i=\varepsilon_{ijk}\partial_j\lambda f_k=\varepsilon_{ijk}(\partial_j\lambda)f_k+\lambda\varepsilon_{ijk}\partial_jf_k=](/upload/math/1/5/f/15f80c722939d5d24dd53873f04b0f4c.png)
![=[\mathrm{grad}\lambda(u)\times f(u)+\lambda(u).\mathrm{rot}f(u)]_i](/upload/math/3/3/c/33c3ed5ec40fd5cce155b403e1e0596f.png)
![[\mathrm{d}(f\cdot g)(u)]_{1j}=\partial_j(f\cdot g)=\partial_j f_kg_k=f_k\partial_j g_k+g_k \partial_j f_k](/upload/math/a/b/e/abe7bd7e0906b512cebfb33fda537ad4.png)
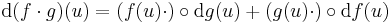
![\mathbf{J}^{f\cdot g}(u)=[f(u)]^\mathrm{T}\cdot \mathbf{J}^g(u) +
[g(u)]^\mathrm{T}\cdot \mathbf{J}^f(u)](/upload/math/0/4/8/048559240cdb9844693361f4d89d42b3.png)