Matematika A2a 2008/6. gyakorlat
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Differenciálhatóság
A többváltozós differenciálhatóságot az egyváltozós alábbi átfogalmazásából általánosítjuk:
Definíció. Legyen f: Rn  Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn
Rm és u ∈ int Dom(f). Azt mondjuk, hogy f differenciálható az u pontban, ha létezik olyan A: Rn  Rm lineáris leképezés, hogy
Rm lineáris leképezés, hogy
Ekkor A egyértelmű és az f leképezés u-bent beli differenciáljának vagy n×n-es esetben deriválttenzorának nevezzük és df(u)-val vagy Df(u)-val jelöljük. Ezt a fogalmat néha teljes differenciálnak, totális differenciálnak vagy Fréchet-deriváltnak is mondjuk.
Megjegyzés. A fenti határérték 0 volta egyenértékű a következő kijelentéssel. Létezik A: Rn  Rm lineáris leképezés és ε: Dom(f)
Rm lineáris leképezés és ε: Dom(f)  Rm függvény, melyre:
Rm függvény, melyre:
- ε folytonos u-ban és ε(u)=0, továbbá
minden x ∈ Dom(f)-re:
Megjegyzés. Azt, hogy A egyértelmű, a következőkkel bizonyíthatjuk. Legyen A és B is a mondott tulajdonságú, azaz létezzenek ε és η az u-ban eltűnő és ott folytonos Dom(f)-en értelmezett függvények, melyekre teljesül, hogy minden x ∈ Dom(f)-re
ezeket kivonva egymásból és használva minden x-re:
így minden x = u + ty értékre is az azonosan nullát kapjuk, ha t pozitív szám, y pedig rögzített nemnulla vektor, azaz minden t-re
az azonosan 0 függény határértéke t 0 esetén szintén nulla:
0 esetén szintén nulla:
hiszen t-t kiemelhetünk és egyszerűsíthetünk és t 0 esetén
ε és η nullává válik.
Ez viszont pont azt jelenti, hogy a két lineéris operátor azonosan egyenlő.
0 esetén
ε és η nullává válik.
Ez viszont pont azt jelenti, hogy a két lineéris operátor azonosan egyenlő.
Jacobi-mátrix
A df(u) lineáris leképezés (e1,e2,...,en) szetenderd bázisbeli mátrixa legyen: [df(u)] = A. Vizsgáljuk mibe viszi a bázisokat df(u) leképezés!
Írjuk fel a definíciót, de az e1 egységvektor mentén tartsunk u-hoz: x = u + te1. Ekkor
ami azért hasznos, mert a
alakból kiemelhetó t:
azaz
vagyis f koordinátafüggvényeinek az első változó szerinti parciális deriváltja az u pontban. A többi oszlopvektor ugyanígy:
amelyet Jacobi-mátrixnak nevezünk.
Következmény. Tehát. ha f totálisan differenciálható, akkor parciálisan is differenciálható és a differenciál sztenderd bázisbeli mátrixa a Jacobi-mátrix.
Azaz:
- teljes differenciálhatóság
 parciális differenciálhatóság
parciális differenciálhatóság
de ez fordítva már nem igaz:
- parciális differenciálhatóság
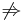 teljes differenciálhatóság
teljes differenciálhatóság
Erre vonatkozik a két alábbi példa.
Folytonosság és totális differenciálhatóság
Tekintsük az
Ekkor
Viszont g nem totálisan diffható, mert a (t,t) mentén a (0,0)-ba tartva:
ami nem létezik.
Megjegyzés. Itt persze g nem folytonos, és itt is igaz az, hogy ha totálisan differenciálható egy függvény, akkor folytonos is:
Tétel. Ha f differenciálható u-ban, akkor ott folytonos is, ugyanis minden x-re:
amely tagjai mind folytonosak u-ban.
Iránymenti deriválhatóság és differenciálhatóság
Példa.
Ekkor
Ha tehát differenciálható, akkor az iránymenti deriváltak (Gateau-deriváltak) is léteznek (e egységvektor):
Ám, polárkoordinátákra áttérve:
φ = π/4-et és π + π/4-et véve a vetületfüggvény a
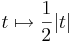 ,
,
ami nem differenciálható a 0-ban.
Lineáris és affin függvény deriváltja
Tétel. Az A : Rn  Rm lineáris leképezés differenciálható és differenciálja minden pontban saját maga:
Rm lineáris leképezés differenciálható és differenciálja minden pontban saját maga:
Ugyanis, legyen u ∈ Rn. Ekkor
Tétel. Az azonosan c konstans függény esetén az dc(u)  0 alkalmas differenciálnak, mert
0 alkalmas differenciálnak, mert
Tehát minden u ∈ Rn-re
Példa
Az A: x  2x1 + 3x2 - 4x3 lineáris leképezés differenciálja az u pontban az u-tól független
2x1 + 3x2 - 4x3 lineáris leképezés differenciálja az u pontban az u-tól független
és Jacobi-mátrixa a konstans
mátrix.
Világos, hogy a
koordináta vagy projekciófüggvény lineáris, differenciálja minden u pontban saját maga és ennek mátrixa:
ahol az 1 az i-edik helyen áll. Másként
ahol
azaz a Kronecker-féle δ szimbólum.
Egyváltozós illetve valós értékű függvény deriváltja
Függvények lineáris kombinációja
Ha f és g a H ⊆ Rn halmazon értelmezett Rm-be képező, az u ∈ H-ban differenciálható függvények, akkor minden λ számra
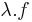 is differenciálható u-ban és
is differenciálható u-ban és 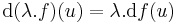 és
és
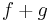 is differenciálható u-ban és
is differenciálható u-ban és 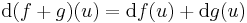
Ugyanis, a mondott differenciálokkal és a
választással, ezek az u-ban folytonosak lesznek és a lineáris résszekel együtt ezek előállítják a skalárszoros és összegfüggvények megváltozásait.
Függvénykompozíció differenciálja
Tétel. Legyen g: Rn ⊃ Rm, az u-ban differenciálható, f: Rm ⊃
Rm, az u-ban differenciálható, f: Rm ⊃ Rk a g(u)-ban differenciálható függvény, u ∈ int Dom(f
Rk a g(u)-ban differenciálható függvény, u ∈ int Dom(f 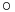 g). Ekkor az
g). Ekkor az
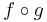 differenciálható u-ban és
differenciálható u-ban és
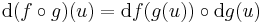
Bizonyítás. Alkalmas ε, A és η B párral, minden x ∈ Dom(f 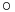 g)-re:
g)-re:
Innen leolvasható a differenciál és a másodrendben eltűnő mennyiség vektortényezője, az
melyben az első tag a 0-hoz tart, mivel a lineáris leképezés a 0-ban folytonos, és η a 0-hoz tart az u-ban. A második tag nulla szor korlátos alakú, hiszen a lineáris leképezés Lipschitz-tuladonsága folytán B minden egységvektoron korlátos értéket vesz fel.
Ennek a tételnek a legegyszerűbb, de már vektorokat tartalmazó formáját írja át "fogyasztható" formába az alábbi
Következmény. Ha g: Rn ⊃ R, az u-ban differenciálható, f: R ⊃
R, az u-ban differenciálható, f: R ⊃ R a g(u)-ban differenciálható függvény, u ∈ int Dom(f
R a g(u)-ban differenciálható függvény, u ∈ int Dom(f 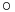 g), akkor
g), akkor
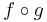 differenciálható u-ban és
differenciálható u-ban és
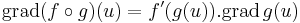
Ahol . a skalárral való szorzást jelöli.
1. Példa
Először a gradienst számítjuk ki. Mivel a gyökfüggvény nem differenciálható a 0-ban, ezért a differenciál csak nemnulla r-re számítható ki. 0-ban a függvény tényleg nem differenciálható, mert a parciális deriváltak nem léteznek.
és
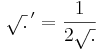 illetve
illetve 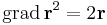
Ezért
Ha valakinek a differenciál leképezés kell, akkor pedig:
Ezek kompozíciója:
Szemléleti okokból lényeges, hogy itt . a skalárral való szorzás,  a skaláris szorzás.
a skaláris szorzás.
2. Példa
illetve a gradiens:
Skalárfüggvények szorzata
λ, μ: H  R, ahol H ⊆ Rn és az u ∈ H-ban mindketten differenciálhatók, akkor λμ is és
R, ahol H ⊆ Rn és az u ∈ H-ban mindketten differenciálhatók, akkor λμ is és
azaz
Példa
Számoljuk ki r2 deriváltját a szorzat szabálya szerint.
Egyrészt, ha r ≠ 0, akkor
Másrészt, ha r = 0, akkor
minden r-re fennáll, így grad(id2)(0) = 0 alkalmas az ε(r)=|r|-rel, tehát r2 differenciálható 0-ban is.
a × ... operátor
Differenciálható-e és ha igen mi a differenciálja, divergenciája, rotációja a
leképezésnek, ahol a előre megadott konstans vektor.
Megoldás
Az a × ..., azaz az
(itt I az identitás leképezés) leképezés lineáris, minthogy a vektoriális szorzás mindkét változójában lineáris (v ∈ Lin(R3;R3)), így differenciálható és differenciálja saját maga:
azaz
minden h és r ∈ R3 vektorra.
Jacobi-mátrixa (a sztenderd bázisbeli mátrixa) tetszőleges (x,y,z) pontban:
Mivel a főátlóbeli elemek mind nullák, ezért ebből rögtön következik, hogy div(a × I)(r) = 0.
azaz rot v (r) = 2a. Az előbb felhasználtuk a kettős vektoriális szorzatra vonatkozó kifejtési tétel indexes alakját, a
ami azt mondja, hogy ha az ijk és klm-ben a nem azonos párok jó sorrendben következnek, akkor az epszolon 1-et, ha rossz sorrendben, akkor -1-et ad.
a  ... operátor
... operátor
Differenciálható-e és ha igen mi a differenciálja
leképezésnek, ahol a előre megadott konstans vektor.
Megoldás
Skalártér lévén Φ gradiensét kell kiszámolnunk. Mivel ez is lineáris leképezés, ezért differenciálható és differenciálja saját maga, azaz a gradiens vektor pont a:
Ezt persze indexes deriválással is kiszámítható:
További példa skalárfüggvényre
Hatérozzuk meg a Φ
(ahol i az x irányú egységvektor, |.| a vektor hossza) függvény szintvonalait, differenciálhatóságát, gradiensét!
Megoldás
Érdemes koordinátás írásmódra áttérni, hiszen az i vektor úgy is a koordinátarendszerhez kapcsolódik. A vektoriális szorzás definíciója miatt
Tehát azok a pontok vannak azonos szintfelületen, melyeknek az [yz] síkra vett vetületük azonos hosszúságú (i × r hossza az i-re merőleges komponense r-nek). Az
- y2 + z2 = 0
egyenlettel megadott pontokban (másként: y = 0 & z = 0 & x tetszőleges) a függvény nem differenciálható, ugyanis a Φ=0 szintfelület elfajúlt módon csak egy egyenes, az x tengely, így a gradiens vektor iránya nem egyértelmű. Ezt azzal is igazolhatjuk, ha vesszük ezekben a pontokban például az y irányú parciális függvényt:
azaz az (x0,0,0) pontokhoz tartozó Φ(x0, . ,0) parciális függvény nem differenciálható a 0-ban.
Máshol a gradiensvektor, a parciális deriváltakat kiszámítva
vagy másként:
Megjegyezzük, hogy ehhez még a függvénykompozíció deriválási szabályával is lejuthattunk volna:
Teljes és parciális differenciálhatóság
Ha az f:Rn ⊃ Rm függvény differenciálható az u pontban, akkor ott minden parciális deriváltja létezik és teljesül [(df(u))ej]i = ∂jfi(u).
Azaz:
Rm függvény differenciálható az u pontban, akkor ott minden parciális deriváltja létezik és teljesül [(df(u))ej]i = ∂jfi(u).
Azaz:
- teljes differenciálhatóság
 parciális differenciálhatóság
parciális differenciálhatóság
de ez fordítva már nem igaz:
- parciális differenciálhatóság
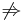 teljes differenciálhatóság
teljes differenciálhatóság
Erre vonatkozik a két alábbi példa.
Nem folytonos függvény létező parciális deriváltakkal
Tekintsük az
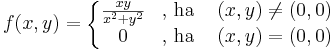
set pm3d
(0,0)-ban a parciális függvények az azonosan 0 függvény, mely persze deriválható a 0-ban, de a függvény még csak nem is folytonos (0,0)-ban, mely szükséges feltétele a teljes differenciálhatóságnak.
További példa
Folytonos parciális differenciálhatóság
Megfordításról a következő esetben beszélhetünk.
Tétel. Ha az f:Rn ⊃ Rm függvény minden parciális deriváltfüggvénye létezik az u egy környezetében és u-ban a parciális deriváltak folytonosak, akkor u-ban f differenciálható. (Sőt, folytonosan differenciálható.)
Rm függvény minden parciális deriváltfüggvénye létezik az u egy környezetében és u-ban a parciális deriváltak folytonosak, akkor u-ban f differenciálható. (Sőt, folytonosan differenciálható.)
Bizonyítás. Elegendő az m = 1 esetet vizsgálni. Továbbá a bizonyítás elve nem változik, ha csak az n = 2 esetet tekintjük. Legyen x az u mondott környezetéből vett pont, és x = (x1,x2), v=(u1,x2), u=(u1,u2) Ekkor az [x,v] szakaszon ∂1f-hez a Lagrange-féle középértéktétel miatt létezik olyan ξ(x1)∈[x1,u1] szám, és a [v,u] szakaszon ∂2f-hez ζ(x2)∈[x2,u2] szám, hogy
itt az
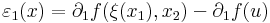 és
és 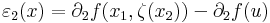
függvények folytonosak u-ban (még ha a ξ, ζ függvények nem is azok), és értékük az u-ban 0. Világos, hogy ez azt jelenti, hogy f differenciálható u-ban.
Világos, hogy a parciális deriváltak folytonossága szükséges a fenti tételben. Az alábbi példában léteznek a parciális deriváltfüggvények az u egy környzetében, de az u-ban nem folytonosak.
Nem differenciálható, nem folytonosan parciálisan differenciálható függvény
parciális deriváltfüggvényei léteznek:
a másik hasonlóan. A 0-ban 0 mindkettő, de az (0,1/n) mentén a 0-ba tartva az 1-hez tart, ami nem 0.
Differenciálható, de nem folytonosan parciálisan differenciálható
A differenciálhatóság azonban nem elég ahhoz, hogy a parciális deriváltak folytonosak legyenek.
Az
differenciálható, hiszen ez az
függvény és r ≠ 0-ban:
és grad f nem korlátos. Ez persze a parciális deriváltakon is megátszik: azok sem korlátosak.
Indexes deriválás
Most csak a sokféle szorzat deriváltjának értékét számítjuk ki. Minden esetben igazolható, hogy ha a formulákban szereplő összes derivált létezik, akkor a formula érvényes (sőt, ha a függvények az adott pontban differenciálhatók, akkor a szorzat is differenciálható az adott pontban). Az mátrixelemeket indexesen számítjuk.
Feltéve például, hogy az f többváltozós skalárfüggvény parciálisan differenciálható, a gradiens elemeit így nyerjük:
1. Példa
Ha f(r) = r2, akkor
de a koordinátafüggvények deriváltjairól tudjuk, hogy azoknak az értékét a Kronecker-delta adja:
azaz
tehát parciálisan differenciálható minden pontban és a Jacobi-mártix elemei a fentiek.
2. Példa
Ha f(r) = ar, akkor
3. Példa
Ha f(r) = |r|α, akkor
itt ne feledjük, hogy k-ra szummázunk és hogy az összetett tényezőben a skaláris szorzat szerepel:
tehát parciálisan differenciálható minden pontban és a Jacobi-mártix elemei a fentiek.
Deriválttenzor és invariánsai
Ha A az f:Rn ⊃ Rn leképezés differenciálja az u pontban, akkor A-t deriválttenzornak nevezzük. Minden tenzor egyértelműen előáll egy szimmetrikus és egy antiszimmetrikus tenzor összegeként:
Rn leképezés differenciálja az u pontban, akkor A-t deriválttenzornak nevezzük. Minden tenzor egyértelműen előáll egy szimmetrikus és egy antiszimmetrikus tenzor összegeként:
Ebből a szimmetrikus rész főátlbeli elemeinek összege minden bázisban ugyanaz a skaláris érték, melyet a tenzor nyomának, illetve a függvény divergenciájának nevezzük:
 illetve
illetve 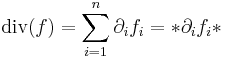
Az utóbbi írásmód a koordinátás alakban az úgy nevezett Einstein-féle jelölési konvenció, amelynek elve, hogy a kétszer stereplő indexekre automatikusan szumma értendő.
Példa
f:R3 ⊃ R3
esetben a tenzor antiszimmetrikus részéhez egyértelműen létezik egy olyan a vektor, hogy minden r-re:
R3
esetben a tenzor antiszimmetrikus részéhez egyértelműen létezik egy olyan a vektor, hogy minden r-re:
mely vektort az f rotációjának nevezzük:
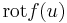 és
és ![[\mathrm{rot}f(u)]_i=\sum\limits_{j,k=1}^3\varepsilon_{ijk}\partial_j f_k=*\varepsilon_{ijk}\partial_j f_k*](/upload/math/b/e/d/bed2ac05c3c84c0a2da64ec31206b3fa.png)
ahol
a Levi-Civita-szimbólum.
Skalárfüggvénnyel való szorzás
λ: H  R, f:H
R, f:H  Rm, ahol H ⊆ Rn és az u ∈ H-ban mindketten differenciálhatók, akkor λ.f is és
Rm, ahol H ⊆ Rn és az u ∈ H-ban mindketten differenciálhatók, akkor λ.f is és
azaz
ahol 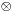 a diadikus szorzat, melynek koordinátamátrixa egy oszlopvektor (balról) és egy sorvektor (jobbról) mátrixszorzatából adódik. Ez ritkán kell teljes egészében, a két invariáns (rot-nál csak 3×3-as esetben) a gyakoribb.
a diadikus szorzat, melynek koordinátamátrixa egy oszlopvektor (balról) és egy sorvektor (jobbról) mátrixszorzatából adódik. Ez ritkán kell teljes egészében, a két invariáns (rot-nál csak 3×3-as esetben) a gyakoribb.
Vektorfüggvények skaláris szorzata
f,g:H  Rm, ahol H ⊆ Rn és az u ∈ H-ban mindketten differenciálhatók, akkor f
Rm, ahol H ⊆ Rn és az u ∈ H-ban mindketten differenciálhatók, akkor f g is és
g is és
azaz
illetve a Jacobi-mátrixszal:
ahol [.]T az oszlopvektor transzponáltját, 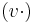 pedig a v vektorral történő skaláris szorzás operátorát jelöli.
pedig a v vektorral történő skaláris szorzás operátorát jelöli.
Házi feladat
-
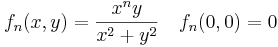 függvényosztály folytonossága parciális és totális deifferenciálhatósága, folytonos parciális és totális differenciálhatósága
függvényosztály folytonossága parciális és totális deifferenciálhatósága, folytonos parciális és totális differenciálhatósága
| 5. gyakorlat | 7. gyakorlat |
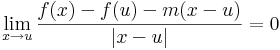

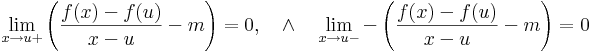
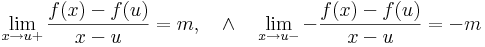
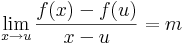
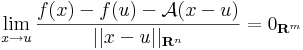
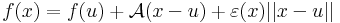
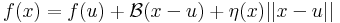
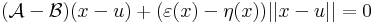
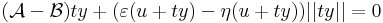
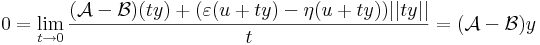
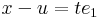
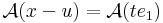
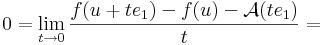
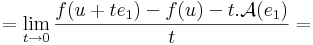
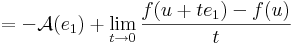
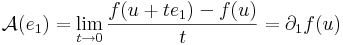
![[\mathrm{d}f(u)]=\mathbf{J}^f(u)=\begin{bmatrix}
\partial_1 f_1(u) & \partial_2 f_1(u) & \dots & \partial_n f_1(u)\\
\partial_1 f_2(u) & \partial_2 f_2(u) & \dots & \partial_n f_2(u)\\
\vdots & \vdots & \ddots & \vdots \\
\partial_1 f_m(u) & \partial_2 f_m(u) & \dots & \partial_n f_m(u)\\
\end{bmatrix}](/upload/math/b/c/8/bc8c1cf3c3d6f5032a7858552cc82a3a.png)
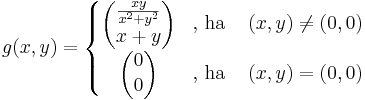
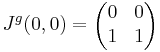
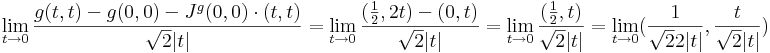
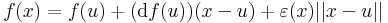
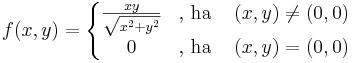
![\mathrm{J}^f(0,0)=[0, 0]\,](/upload/math/5/8/4/5844bda58422be338e9d02beef5b1e3e.png)
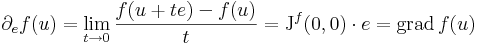
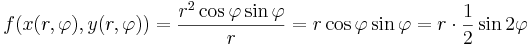
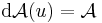
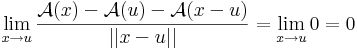
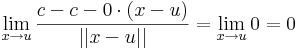

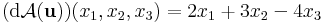
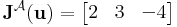
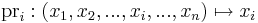
![[\mathrm{grad}\,\mathrm{pr_i}]=\mathbf{J}^{\mathrm{pr}_i}(\mathbf{u})=\begin{bmatrix}0 & 0 & ... & 1 & ...& 0\end{bmatrix}](/upload/math/f/a/5/fa51c1bb60d1e414a5acb5c8e93ae7d2.png)
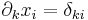
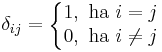
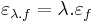
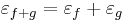
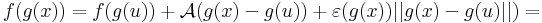
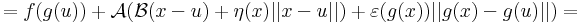
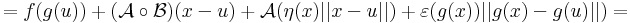
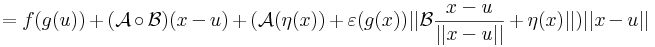
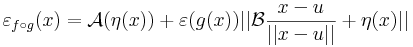
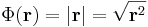
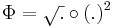
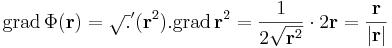
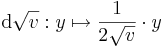
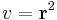
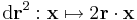
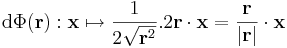
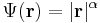
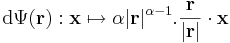
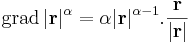
![[\mathrm{d}(\lambda\mu)(u)]_{1j}=\partial_j(\lambda\mu)=\mu\partial_j\lambda+\lambda\partial_j\mu=[\mu(u).\mathrm{grad}\,\lambda(u)+\lambda(u).\mathrm{grad}\,\mu(u)]_{j}](/upload/math/c/0/6/c06d0e7630e5abf100915f67de31ed5d.png)
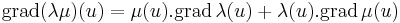
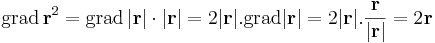
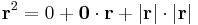
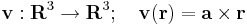
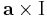
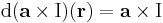
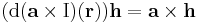
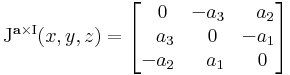
![[\mathrm{rot}\,\mathbf{v}]_i=\varepsilon_{ijk}\partial_j\varepsilon_{klm}a_lx_m=\varepsilon_{ijk}\varepsilon_{klm}a_l\partial_j x_m=\varepsilon_{ijk}\varepsilon_{klm}a_l\delta_{jm}=\varepsilon_{ijk}\varepsilon_{klj}a_l=](/upload/math/6/4/2/642b95a997703a68637ff5897331d591.png)
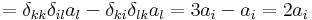
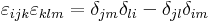
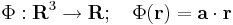
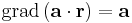
![[\mathrm{grad}\,\Phi]_i=\partial_ia_kx_k=a_k\partial_ix_k=a_k\delta_{ik}=a_i\,](/upload/math/e/6/7/e67c528d00633fe5efe34a67e9c2aef9.png)
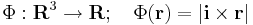
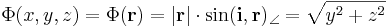
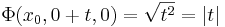
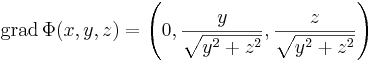
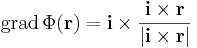
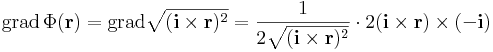
![f(x,y)=\sqrt[3]{x^3+y^3}](/upload/math/0/1/e/01ea4c71d858e4427120d46ec42ac8ea.png)
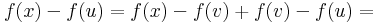
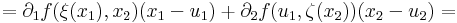
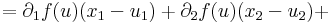
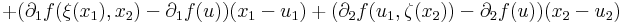
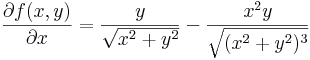
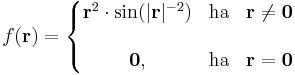
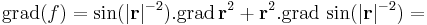
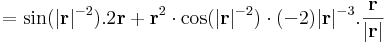
![[\mathrm{grad}\,f]_i=\partial_if\,](/upload/math/f/a/3/fa3c940fa1fad80ffb905f790caa7495.png)
![\mathbf{r}^2=\sum\limits_{k=1}^3 [\mathbf{r}]_k[\mathbf{r}]_k=\sum\limits_{k=1}^3 x_kx_k=[\mathrm{Einstein\;konv.}]\;x_kx_k](/upload/math/d/8/b/d8b7a2ddcfd984008eedaf9f2fc25505.png)
![[\mathrm{grad}\,f]_i=\partial_ix_kx_k\,=x_k\partial_ix_k+x_k\partial_ix_k\,](/upload/math/9/c/7/9c7478f0fc6c90cb7d94d0f617d8d49a.png)
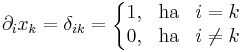
![[\mathrm{grad}\,f]_i=2x_k\delta_{ik}=2x_i=[2\mathbf{r}]_i\,](/upload/math/d/7/8/d784a387f1c950a3e0e038cc56a61cbd.png)
![[\mathrm{grad}\,f]_i=\partial_ia_kx_k\,=a_k\partial_ix_k=a_k\delta_{ik}\,=a_i=[\mathbf{a}]_i](/upload/math/a/5/7/a57f9bc5e37f361c19f92eee518f6f06.png)
![[\mathrm{grad}\,f]_i=\partial_i(x_kx_k)^{\alpha/2}\,=\partial_i(x_k)^{\alpha}=\frac{\alpha}{2}(x_kx_k)^{\frac{\alpha}{2}-1}2\delta_{ik}x_k\,](/upload/math/7/1/8/71892bcadec17b766681f84d469b9ff3.png)
![[\mathrm{grad}\,f]_i=\alpha(x_kx_k)^{\frac{\alpha}{2}-1}x_i\,=\left[\alpha|\mathbf{r}|^\alpha\frac{\mathbf{r}}{\mathbf{r}^2}\right]_i=\left[\alpha|\mathbf{r}|^{\alpha-1}\frac{\mathbf{r}}{|\mathbf{r}|}\right]_i](/upload/math/0/d/e/0ded0710fdc3c526de84bc11a3747b26.png)
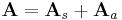
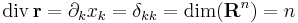
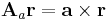
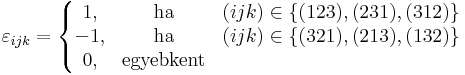
![[\mathrm{d}(\lambda.f)(u)]_{ij}=\partial_j(\lambda.f)=\partial_j\lambda f_i=f_i\partial_j\lambda+\lambda \partial_jf_i](/upload/math/3/f/f/3ff67b8cf3567d0fa54ce6ef1b76ee50.png)
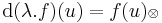
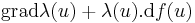
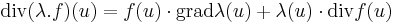
![[\mathrm{rot}(\lambda.f)(u)]_i=\varepsilon_{ijk}\partial_j\lambda f_k=\varepsilon_{ijk}(\partial_j\lambda)f_k+\lambda\varepsilon_{ijk}\partial_jf_k=](/upload/math/1/5/f/15f80c722939d5d24dd53873f04b0f4c.png)
![=[\mathrm{grad}\lambda(u)\times f(u)+\lambda(u).\mathrm{rot}f(u)]_i](/upload/math/3/3/c/33c3ed5ec40fd5cce155b403e1e0596f.png)
![[\mathrm{d}(f\cdot g)(u)]_{1j}=\partial_j(f\cdot g)=\partial_j f_kg_k=f_k\partial_j g_k+g_k \partial_j f_k](/upload/math/a/b/e/abe7bd7e0906b512cebfb33fda537ad4.png)
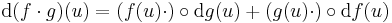
![\mathbf{J}^{f\cdot g}(u)=[f(u)]^\mathrm{T}\cdot \mathbf{J}^g(u) +
[g(u)]^\mathrm{T}\cdot \mathbf{J}^f(u)](/upload/math/0/4/8/048559240cdb9844693361f4d89d42b3.png)