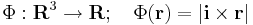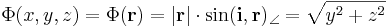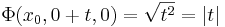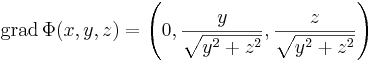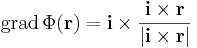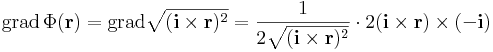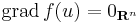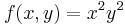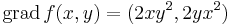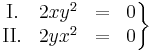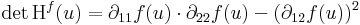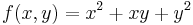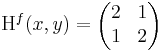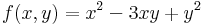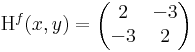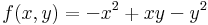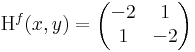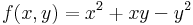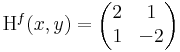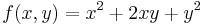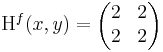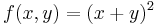Matematika A2a 2008/7. gyakorlat
Mozo (vitalap | szerkesztései) (→Feltételes és tartományi szélsőérték) |
Mozo (vitalap | szerkesztései) |
||
| 235. sor: | 235. sor: | ||
</gnuplot> | </gnuplot> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
A lap 2008. április 10., 22:17-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Tartalomjegyzék |
a × ... operátor
Differenciálható-e és ha igen mi a differenciálja, divergenciája, rotációja a
leképezésnek, ahol a előre megadott konstans vektor.
Megoldás
Az a × ..., azaz az
(itt I az identitás leképezés) leképezés lineáris, minthogy a vektoriális szorzás mindkét változójában lineáris (v ∈ Lin(R3;R3)), így differenciálható és differenciálja saját maga:
azaz
minden h és r ∈ R3 vektorra.
Jacobi-mátrixa (a sztenderd bázisbeli mátrixa) tetszőleges (x,y,z) pontban:
Mivel a főátlóbeli elemek mind nullák, ezért ebből rögtön következik, hogy div(a × I)(r) = 0.
azaz rot v (r) = 2a. Az előbb felhasználtuk a kettős vektoriális szorzatra vonatkozó kifejtési tétel indexes alakját, a
ami azt mondja, hogy ha az ijk és klm-ben a nem azonos párok jó sorrendben következnek, akkor az epszolon 1-et, ha rossz sorrendben, akkor -1-et ad.
a  ... operátor
... operátor
Differenciálható-e és ha igen mi a differenciálja
leképezésnek, ahol a előre megadott konstans vektor.
Megoldás
Skalártér lévén Φ gradiensét kell kiszámolnunk. Mivel ez is lineáris leképezés, ezért differenciálható és differenciálja saját maga, azaz a gradiens vektor pont a:
Ezt persze indexes deriválással is kiszámítható:
További példa skalárfüggvényre
Hatérozzuk meg a Φ
(ahol i az x irányú egységvektor, |.| a vektor hossza) függvény szintvonalait, differenciálhatóságát, gradiensét!
Megoldás
Érdemes koordinátás írásmódra áttérni, hiszen az i vektor úgy is a koordinátarendszerhez kapcsolódik. A vektoriális szorzás definíciója miatt
Tehát azok a pontok vannak azonos szintfelületen, melyeknek az [yz] síkra vett vetületük azonos hosszúságú (i × r hossza az i-re merőleges komponense r-nek). Az
- y2 + z2 = 0
egyenlettel megadott pontokban (másként: y = 0 & z = 0 & x tetszőleges) a függvény nem differenciálható, ugyanis a Φ=0 szintfelület elfajúlt módon csak egy egyenes, az x tengely, így a gradiens vektor iránya nem egyértelmű. Ezt azzal is igazolhatjuk, ha vesszük ezekben a pontokban például az y irányú parciális függvényt:
azaz az (x0,0,0) pontokhoz tartozó Φ(x0, . ,0) parciális függvény nem differenciálható a 0-ban.
Máshol a gradiensvektor, a parciális deriváltakat kiszámítva
vagy másként:
Megjegyezzük, hogy ehhez még a függvénykompozíció deriválási szabályával is lejuthattunk volna:
Többváltozós függvény szélsőértéke
Szélsőérték szükséges feltétele
Tétel - Fermat-tétel - Legyen f: Rn 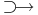 R, u ∈ int Dom(f), f differenciálható u-ban.
R, u ∈ int Dom(f), f differenciálható u-ban.
- Ha u-ban f-nek (lokális) szélsőértéke van, akkor
U.is: minden i-re az i-edik parciális függvénynek szélsőértéke van ui-ben, így az egyváltozós Fermat-tétel miatt ezeknek a deriváltja ui-ben 0, így a gradiens értéke 0.
Példa
Ennek gradiense:
Az
egyenletrendszer megoldásai: x = 0, y tetszőleges ill. y = 0 és x tetszőleges. A szélsőértékek helyei csak ezek közül kerülhetnek ki és ezek valóban szélsőértékek is, mert ezeken a függvény 0-t vesz fel, ami a lehetséges legkisebb értéke.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot 5*x*x*y*y
Másodikderivált próba
Kétszer differenciálható függvényre vonatkozóan megfogalmazhatjuk a lokális maximum és minimum létezésének elégséges feltételét. Csak a kétváltozós függvényekkel foglalkozunk. Tegyük fel, hogy grad f(u) = 0 és Hf(u) az f Hesse-mátrixa
- ha det Hf(u) > 0 és ∂11f(u) < 0, akkor f-nek u-ban maximuma van
- ha det Hf(u) > 0 és ∂11f(u) > 0, akkor f-nek u-ban minimuma van
- ha det Hf(u) < 0, akkor f-nek biztosan nincs szélsőértéke, ún. nyeregpontja van
- ha det Hf(u) = 0, akkor a próba nem járt sikerrel, azaz további vizsgálatokat igényel annak eldöntése, hogy u szélsőérték hely-e.
Megjegyzések. Mivel kétváltozós esetben
ezért olyan eset nem létezik, hogy det Hf(u) > 0 és ∂11f(u) = 0.
Világos, hogy a másodikderivált tipikusan azoknál a függvényeknél jár sikerrel, melyeket egy másodfokú függvény közelít a legjobban (aszimptotikusan másodfokúak). Ha a függvény ennél magasabb fokú, akkor a második deriváltak eltűnnek és a Hesse-mártix elfajul (vagy legalább is tipikusan elfajul).
Ha tehát
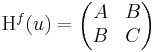 , akkor
, akkor 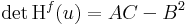 ,
,
és így a tipikus példák a következők.
Példák
1. Ha B kicsi, azaz az AC-hez képest kis abszolútrétékű szám, akkor a szélsőérték irányába mozdul el a feladat.
Ekkor grad f = ( 2x + y , 2y + x ) és
azaz 4 - 1 = 3 > 0 és 2 > 0 miatt minimum.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot x*x+x*y+y*y
2. Ha |B| nagy (azaz AC-hez képest nagy), akkor a bizonyosan nemszélsőérték irányába.
Ekkor grad f = ( 2x + -3y , 2y + -3x ) és
azaz 4 - 9 = -5 < 0 miatt nincs szélsőérték: nyeregpont.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot x*x -3*x*y+y*y
3. Negatív A és C-re és kis B-re:
Ekkor grad f = ( -2x + 3y , -2y + 3x ) és
azaz 4 - 1 = 3 > 0 és -2 < 0 miatt maximum.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot -x*x +x*y-y*y
4. Ha A és C előjele ellenkező, akkor rögtön következik, hogy nincs sz.é.
Ekkor grad f = ( 2x + y , -2y + x ) és
azaz -4 - 1 = -5 < 0 azaz nyeregpont.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot x*x +x*y-y*y
5. Atipikus eset, ha AC = B2. Ekkor nem jár sikerrel a próba:
Ekkor grad f = ( 2x + 2y , 2y + 2x ) és
azaz 4 - 4 = 0, azaz határozatlan eset. De tudjuk, hogy
ami pontosan akkor minimális, ha x = -y, azaz ezeken a helyeken van szélsőérték.
set pm3d
set size 0.8,0.8 set xrange [-1:1] set yrange [-1:1] set zrange [-2:2] set view 50,30,1,1 unset xtics unset ytics unset ztics unset key unset colorboxsplot (x+y)*(x+y)
| 6. gyakorlat | 8. gyakorlat |
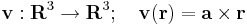
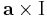
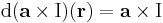
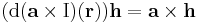
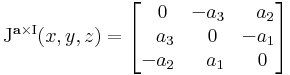
![[\mathrm{rot}\,\mathbf{v}]_i=\varepsilon_{ijk}\partial_j\varepsilon_{klm}a_lx_m=\varepsilon_{ijk}\varepsilon_{klm}a_l\partial_j x_m=\varepsilon_{ijk}\varepsilon_{klm}a_l\delta_{jm}=\varepsilon_{ijk}\varepsilon_{klj}a_l=](/upload/math/6/4/2/642b95a997703a68637ff5897331d591.png)
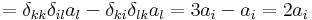
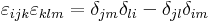
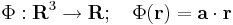
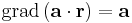
![[\mathrm{grad}\,\Phi]_i=\partial_ia_kx_k=a_k\partial_ix_k=a_k\delta_{ik}=a_i\,](/upload/math/e/6/7/e67c528d00633fe5efe34a67e9c2aef9.png)