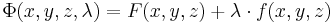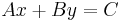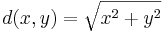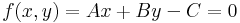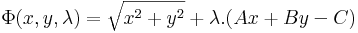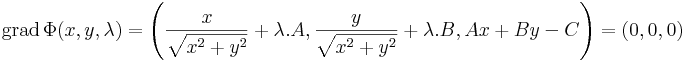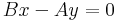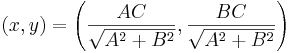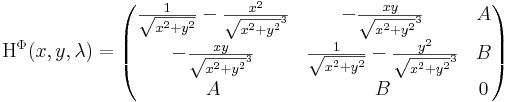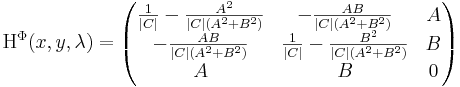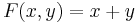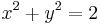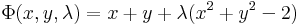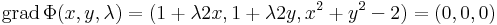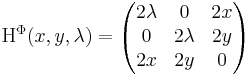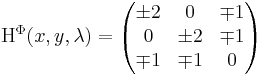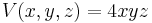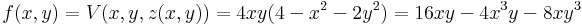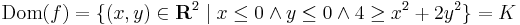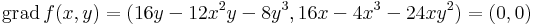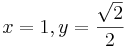Matematika A2a 2008/8. gyakorlat
Tartalomjegyzék |
Feltételes szélsőértékfeladat
Feltétele szélsőérték feladat - Lagrange-multiplikátormódszer - Tegyük fel, hogy az u = F(x,y,z) skalárfüggvény szélsőértékét keressük az f(x,y,z) = c korlátozás (feltétel) mellett. Ekkor a következőképpen járunk el. A szükségesség szempontjából a feladat egyenértékű az
négyváltozós szélsőérték feladat vizsgálatával.
1. példa
Határozzuk meg a síkon az origó távolságát egy adott egyenesől!
Legyen az egyenes egyenlete
(nyilván A és B nem egyszerre nulla, mert (A,B) nomálvektor.) A keresett szám az origó és az egyenes pontjai közötti távolságok közül a legkisebb.
Tehát keressük a
kétváltozós leképezés minimumát az
feltétel mellett.
Megjegyzés. Ez a minimum biztosan létezik, mert ha P az egyenes egy tetszőlegesen rögzített pontja, akkor az OP távolság kétszeresénél közelebb lesz a keresett szélsőértékhely. A feladat tehát az 2 OP sugarú zárt gömb és az egyenes közös pontjain értelmezett, fenti d(x,y) hozzárendelési utasítású függvény szélsőértékének meghatérozása. d kompakt halmazon folytonos, így Weierstrass tétele miatt felveszi abszolút minimumát.
OP sugarú zárt gömb és az egyenes közös pontjain értelmezett, fenti d(x,y) hozzárendelési utasítású függvény szélsőértékének meghatérozása. d kompakt halmazon folytonos, így Weierstrass tétele miatt felveszi abszolút minimumát.
Lagrange módszere szerint a feltételi egyenlet nullára redukált alakja:
ezt a leképezést kell hozzávenni a multiplikátorral szorozva a függvényhez:
Az szélsőérték szükségességét vizsgálva:
Az utolsó 0 lényegében a feltételi egyenlet megismétlését jelenti. λ kiesik, ha az első "egyenlet" B-vel, a másodikat A-val beszorozzuk. Ebből:
és a feltételi egyenlet:
Innen
Annak eldöntése, hogy ez valóban minimumhely-e, a második derivált próbára hárulna, de az nem tudja eldönteni mert (mint kiderülne) a Hesse-mátrix nem nem definit.
az adott pontban ez
A bal felső elem pozitív, de a 2×2-es determináns nulla. Azaz a szabad feladat szemidefinit és a szélsőérték jellegének megvizsgálása további tanulmányozást igényelne, amit most idő hiányában nem végzünk el.
2. példa
Keressük az
összeg maximumát az
feltétel mellett.
Legyen
Ekkor
így
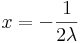 ,
, 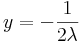 ,
, 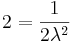
Innen a megoldások:
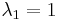 ,
, 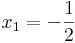 ,
, 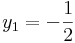
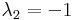 ,
, 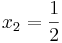 ,
, 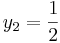
A Hesse-mátrix:
az adott pontokban ez
A két megoldás esetén a szabad probléma aldeterminánsai:
- 2, 4
- -2, 4
azaz már a szabad feladat 2×2-es mátrixa is pozitív ill. negatív definit, azaz nyugodtan kijelenthetjük, hogy feltételes feldatnak (-1/2,-1/2)-ben minimuma, (1/2,1/2)-ben maximuma van.
Tartományi szélsőértékfeladat
Legyen K ⊆ Rn kompakt halmaz és f : Rn R differenciálható függvény. Weierstrass tétele szerint f felveszi szélsőértékeit. Ha int (K)-ban nem találunk lokális szélsőértékhelyet, akkor a határon veszi föl azokat, melyet a multiplikátormódszerrel, vagy egyéb feltételes szélsőértékmódszerrel számolunk ki. Ha int(K)-ban van lokális szélsőérték, akkor a front(K) szélsőértékei és eközött kell megtalálnunk az extémumot.
R differenciálható függvény. Weierstrass tétele szerint f felveszi szélsőértékeit. Ha int (K)-ban nem találunk lokális szélsőértékhelyet, akkor a határon veszi föl azokat, melyet a multiplikátormódszerrel, vagy egyéb feltételes szélsőértékmódszerrel számolunk ki. Ha int(K)-ban van lokális szélsőérték, akkor a front(K) szélsőértékei és eközött kell megtalálnunk az extémumot.
1. példa
Tekintsük a
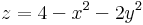 egyenletű elliptikus paraboloidot. Határozzuk meg a [-x,x], [-y,y], [0,z] élek által kifeszített legnagyobb térfogatú tégla térfogatát, ha (x,y,z) a felületen, az [x,y] sík feletti részen van.
egyenletű elliptikus paraboloidot. Határozzuk meg a [-x,x], [-y,y], [0,z] élek által kifeszített legnagyobb térfogatú tégla térfogatát, ha (x,y,z) a felületen, az [x,y] sík feletti részen van.
Felírjuk a térfogat x,y-tóli függését:
az értelmezési tartománya pedig az első negyed
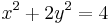 azaz
azaz 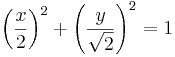
egyenletű ellipszisbe eső része:
Ekkor az int(K) beli szélsőérték szükséges feltétele:
A megoldás
Mivel itt z(x,y) = 2 < 4, ezért (x,y) ∈ int(K) és értéke 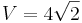 Megállapítjuk, hogy ez maximum és csakis ez. Egyrészt front(K)-n f = 0, így a határon nem veheti föl abszolút maximumát. De belül máshol se, csak az előbbi (x,y) pontban, tehát az a maximum.
Megállapítjuk, hogy ez maximum és csakis ez. Egyrészt front(K)-n f = 0, így a határon nem veheti föl abszolút maximumát. De belül máshol se, csak az előbbi (x,y) pontban, tehát az a maximum.
Megjegyezzük, hogy azt, hogy ez lokális maximum még a másodikderivált próbával is sikeresen ellenőrizhető.
| 7. gyakorlat | 9. gyakorlat |