Matematika A2a 2008/9. gyakorlat
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Kétváltozós függvény integrálása téglán) |
Mozo (vitalap | szerkesztései) (→Kétváltozós függvény integrálása téglán) |
||
| 3. sor: | 3. sor: | ||
Az f(x,y) kétváltozós függvény intergálja tengelyekkel párhuzamos oldalú téglalap alakú tartományon nem függ az integrálás sorrendjétől. Ezesetben a "másik változót" mindig konstansnak vesszük: | Az f(x,y) kétváltozós függvény intergálja tengelyekkel párhuzamos oldalú téglalap alakú tartományon nem függ az integrálás sorrendjétől. Ezesetben a "másik változót" mindig konstansnak vesszük: | ||
:<math>\int\limits_{[a,b]\times[c,d]}f=\int\limits_{x=a}^b\left(\int\limits_{y=c}^d f(x,y)\;\mathrm{d}y\right)\mathrm{d}x=\int\limits_{x=a}^b\int\limits_{y=c}^d f(x,y)\;\mathrm{d}y\mathrm{d}x=\int\limits_{y=c}^d\left(\int\limits_{x=a}^b f(x,y)\;\mathrm{d}x\right)\mathrm{d}y</math> | :<math>\int\limits_{[a,b]\times[c,d]}f=\int\limits_{x=a}^b\left(\int\limits_{y=c}^d f(x,y)\;\mathrm{d}y\right)\mathrm{d}x=\int\limits_{x=a}^b\int\limits_{y=c}^d f(x,y)\;\mathrm{d}y\mathrm{d}x=\int\limits_{y=c}^d\left(\int\limits_{x=a}^b f(x,y)\;\mathrm{d}x\right)\mathrm{d}y</math> | ||
| − | + | ===Példa 1.=== | |
| + | Ha f(x,y) = x és a [0,2]×[0,2]-n integráljuk, akkor először az y szerinti integrált elvégezve (eközben x állandónak minősül), majd a határozott integrált kiszámolva az x szerintit integrálva: | ||
: <math>\int\limits_{x=0}^2\int\limits_{y=0}^2x\;\mathrm{d}y\mathrm{d}x=\int\limits_{x=0}^2\left(\int\limits_{y=0}^2x\;\mathrm{d}y\right)\mathrm{d}x=</math> | : <math>\int\limits_{x=0}^2\int\limits_{y=0}^2x\;\mathrm{d}y\mathrm{d}x=\int\limits_{x=0}^2\left(\int\limits_{y=0}^2x\;\mathrm{d}y\right)\mathrm{d}x=</math> | ||
:<math>=\int\limits_{x=0}^2[xy]_{y=0}^{2}\mathrm{d}x=\int\limits_{x=0}^2 2x\;\mathrm{d}x=[x^2]_{x=0}^{2}=4</math> | :<math>=\int\limits_{x=0}^2[xy]_{y=0}^{2}\mathrm{d}x=\int\limits_{x=0}^2 2x\;\mathrm{d}x=[x^2]_{x=0}^{2}=4</math> | ||
| 10. sor: | 11. sor: | ||
ahol F az f primitív függvénye (vagy határozatlan integrálja). Az eslő esetben az y változó szerepeltetése az integrál kiszámítását követően indokolatlanná vált, de az x megmaradt, amit tovább kellet integrálni az x változóra vonatkozóan. Fordított esetben szintén 4-et kapunk: | ahol F az f primitív függvénye (vagy határozatlan integrálja). Az eslő esetben az y változó szerepeltetése az integrál kiszámítását követően indokolatlanná vált, de az x megmaradt, amit tovább kellet integrálni az x változóra vonatkozóan. Fordított esetben szintén 4-et kapunk: | ||
: <math>\int\limits_{y=0}^2\int\limits_{x=0}^2x\;\mathrm{d}x\mathrm{d}y=\int\limits_{y=0}^2\left(\int\limits_{x=0}^2x\;\mathrm{d}x\right)\mathrm{d}y=</math> | : <math>\int\limits_{y=0}^2\int\limits_{x=0}^2x\;\mathrm{d}x\mathrm{d}y=\int\limits_{y=0}^2\left(\int\limits_{x=0}^2x\;\mathrm{d}x\right)\mathrm{d}y=</math> | ||
| − | :<math>=\int\limits_{y=0}^2[\frac{x^2}{2}]_{x=0}^{2}\mathrm{d}y=\int\limits_{y=0}^22\mathrm{d}y=[2y]_{y=0}^{2}=4</math> | + | :<math>=\int\limits_{y=0}^2\left[\frac{x^2}{2}\right]_{x=0}^{2} \;\mathrm{d}y=\int\limits_{y=0}^22\;\mathrm{d}y=[2y]_{y=0}^{2}=4</math> |
A lap 2008. április 18., 20:32-kori változata
- Ez az szócikk a Matematika A2a 2008 alszócikke.
Kétváltozós függvény integrálása téglán
Az f(x,y) kétváltozós függvény intergálja tengelyekkel párhuzamos oldalú téglalap alakú tartományon nem függ az integrálás sorrendjétől. Ezesetben a "másik változót" mindig konstansnak vesszük:
![\int\limits_{[a,b]\times[c,d]}f=\int\limits_{x=a}^b\left(\int\limits_{y=c}^d f(x,y)\;\mathrm{d}y\right)\mathrm{d}x=\int\limits_{x=a}^b\int\limits_{y=c}^d f(x,y)\;\mathrm{d}y\mathrm{d}x=\int\limits_{y=c}^d\left(\int\limits_{x=a}^b f(x,y)\;\mathrm{d}x\right)\mathrm{d}y](/upload/math/e/f/1/ef10affe1fac157d5fb4427a3a83163c.png)
Példa 1.
Ha f(x,y) = x és a [0,2]×[0,2]-n integráljuk, akkor először az y szerinti integrált elvégezve (eközben x állandónak minősül), majd a határozott integrált kiszámolva az x szerintit integrálva:
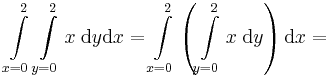
![=\int\limits_{x=0}^2[xy]_{y=0}^{2}\mathrm{d}x=\int\limits_{x=0}^2 2x\;\mathrm{d}x=[x^2]_{x=0}^{2}=4](/upload/math/4/d/7/4d76d92326d729d8a5d68cc30b7ab6c6.png)
Hangsúlyozzuk, hogy itt két esetben a Newton-Leibniz-formulát használtuk a határozott integrál kiszámítására:
![=\int\limits_{a}^b f(x)\mathrm{d}x=[F(x)]_{a}^{b}=F(b)-F(a)](/upload/math/9/7/8/978adb25b56647fca21c75b71c0e4a27.png)
ahol F az f primitív függvénye (vagy határozatlan integrálja). Az eslő esetben az y változó szerepeltetése az integrál kiszámítását követően indokolatlanná vált, de az x megmaradt, amit tovább kellet integrálni az x változóra vonatkozóan. Fordított esetben szintén 4-et kapunk:
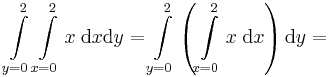
![=\int\limits_{y=0}^2\left[\frac{x^2}{2}\right]_{x=0}^{2} \;\mathrm{d}y=\int\limits_{y=0}^22\;\mathrm{d}y=[2y]_{y=0}^{2}=4](/upload/math/1/a/c/1ac20b7ea17e50cca88da80de185aa12.png)
| 8. gyakorlat | 10. gyakorlat |
