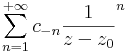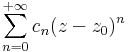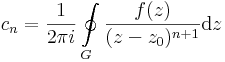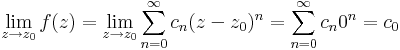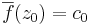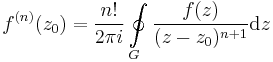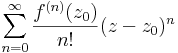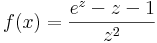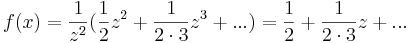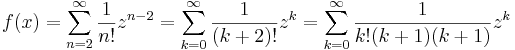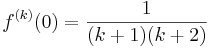Matematika A3a 2008/10. gyakorlat
Mozo (vitalap | szerkesztései) (→Laurent-sor) |
Mozo (vitalap | szerkesztései) |
||
| 1. sor: | 1. sor: | ||
''<sub><[[Matematika A3a 2008]]</sub>'' | ''<sub><[[Matematika A3a 2008]]</sub>'' | ||
| − | + | ==Taylor-sor== | |
| − | + | ||
| − | + | ||
A Cauchy-féle integrálformula következménye a következő tétel, mely a komplex differenciálelmélet egyik megjellegzetesebb eredménye: | A Cauchy-féle integrálformula következménye a következő tétel, mely a komplex differenciálelmélet egyik megjellegzetesebb eredménye: | ||
| 31. sor: | 29. sor: | ||
'''3. ''' Mint minden hatványsor ez is egyenletesen konvergál az összegfüggvényéhez, így tagonként deriválható és integrálható. | '''3. ''' Mint minden hatványsor ez is egyenletesen konvergál az összegfüggvényéhez, így tagonként deriválható és integrálható. | ||
| − | + | ==Laurent-sor== | |
A következőkben olyan függvényekkel foglalkozunk, melyek egy adott pontban nem feltétlenül regulárisak, de azon kívül egy környzetben azok. | A következőkben olyan függvényekkel foglalkozunk, melyek egy adott pontban nem feltétlenül regulárisak, de azon kívül egy környzetben azok. | ||
| 41. sor: | 39. sor: | ||
sor előállítja ''f''-et. | sor előállítja ''f''-et. | ||
| − | + | ===A körgyűrű sugarai=== | |
:<math>R_+=\frac{1}{\limsup\limits_{n>0}\sqrt[n]{|c_n|}}\,</math> | :<math>R_+=\frac{1}{\limsup\limits_{n>0}\sqrt[n]{|c_n|}}\,</math> | ||
:<math>R_-=\limsup\limits_{n<0}\sqrt[n]{|c_n|}\,</math> | :<math>R_-=\limsup\limits_{n<0}\sqrt[n]{|c_n|}\,</math> | ||
| − | + | ===Reguláris- és főrész === | |
| + | A Laurent-sor | ||
:<math>\sum\limits_{n=1}^{+\infty}c_{-n}\frac{1}{z-z_0}^n\,</math> | :<math>\sum\limits_{n=1}^{+\infty}c_{-n}\frac{1}{z-z_0}^n\,</math> | ||
részét a sor '''főrészének,''' a | részét a sor '''főrészének,''' a | ||
| 52. sor: | 51. sor: | ||
részét a sor '''reguláris''' részének nevezzük. | részét a sor '''reguláris''' részének nevezzük. | ||
| − | + | ===A Laurent-sor együtthatói=== | |
:<math>c_n=\frac{1}{2\pi i}\oint\limits_{G}\frac{f(z)}{(z-z_0)^{n+1}}\mathrm{d}z</math> | :<math>c_n=\frac{1}{2\pi i}\oint\limits_{G}\frac{f(z)}{(z-z_0)^{n+1}}\mathrm{d}z</math> | ||
| + | amennyiben a G egy a körgyűrűben haladó a <math>z_0</math>-t egyszer körülölelő zárt görbe. | ||
| − | + | ===Főrész nélküli Laurent-sor=== | |
| + | Ha nincs a Laurent-sornak főrésze, akkor R<sub>-</sub>=0 és az ''f'' függvény a <math>z_0</math> pontban vagy reguláris, vagy megszüntethető szakadása van. Ez utóbbi amiatt, hogy ebben az esetben ''f'' a <math>z_0</math>-on kívül azonos egy hatványsor összegfüggvényével, mely azonban Abel tétele miatt folytonos és így határértéke a helyettesítési értékkel egyenlő. Tehát, ha ''f'' ilyen, akkor: | ||
:<math>\lim\limits_{z\to z_0}f(z)=\lim\limits_{z\to z_0}\sum\limits_{n=0}^\infty c_n(z-z_0)^n=\sum\limits_{n=0}^\infty c_n0^n=c_0</math> | :<math>\lim\limits_{z\to z_0}f(z)=\lim\limits_{z\to z_0}\sum\limits_{n=0}^\infty c_n(z-z_0)^n=\sum\limits_{n=0}^\infty c_n0^n=c_0</math> | ||
hiszen a hatványsoroknál a középpontban a 0<sup>0</sup> hatványt 1-nek értelmezzük. | hiszen a hatványsoroknál a középpontban a 0<sup>0</sup> hatványt 1-nek értelmezzük. | ||
| 61. sor: | 62. sor: | ||
''f'' kiterjeszthető ezek szerint analitikusan kiterjeszthető és az értéke | ''f'' kiterjeszthető ezek szerint analitikusan kiterjeszthető és az értéke | ||
:<math>\overline{f}(z_0)=c_0</math> | :<math>\overline{f}(z_0)=c_0</math> | ||
| − | + | ||
| − | + | Világos, hogy ezesetben a <math>c_n</math> együtthatók pontosan az ''f'' kiterjesztésének '''Taylor-sori együtthatói,''' hiszen a deriváltakra vonatkozó Cauchy-formulákat a Taylor-sorral összevetve: | |
| − | + | ||
| − | + | ||
::<math>f^{(n)}(z_0)=\frac{n!}{2\pi i}\oint\limits_{G}\frac{f(z)}{(z-z_0)^{n+1}}\mathrm{d}z</math> | ::<math>f^{(n)}(z_0)=\frac{n!}{2\pi i}\oint\limits_{G}\frac{f(z)}{(z-z_0)^{n+1}}\mathrm{d}z</math> | ||
::<math>\sum\limits_{n=0}^\infty\frac{f^{(n)}(z_0)}{n!}(z-z_0)^n</math> | ::<math>\sum\limits_{n=0}^\infty\frac{f^{(n)}(z_0)}{n!}(z-z_0)^n</math> | ||
bármilyen a <math>z_0</math>-t egyszer körülölelő, a körgyűrűben haladó zárt görbére. | bármilyen a <math>z_0</math>-t egyszer körülölelő, a körgyűrűben haladó zárt görbére. | ||
| − | + | '''Példa.''' Igazoljuk, hogy az alábbi függvény reguláris a 0 pontban és számítsuk ki a a kiterjesztés összes magasabbrendű deriváltját! | |
| − | + | :<math>f(x)=\frac{e^z-z-1}{z^2}\,</math> | |
| + | ''Megoldás.'' Elvileg ez egy Laurent-sor, hisz számlálóbeli reguláris függvény van elosztva <math>z^2</math>-tel. De konkrétan elvégezve: | ||
| + | :<math>f(x)=\frac{1}{z^2}(\frac{1}{2}z^2+\frac{1}{2\cdot 3}z^3+...)=\frac{1}{2}+\frac{1}{2\cdot 3}z+...</math> | ||
| + | azaz ''f'' a 0-t kivéve egy reguláris függvénnyel egyenlő, azaz kiterjeszthető regulárissá és ez a fenti. A deriváltakat a Taylor-sor együtthatói adják a megfelelő faktoriálissal megsorozva. k=n-2-re: | ||
| + | :<math>f(x)=\sum\limits_{n=2}^{\infty}\frac{1}{n!}z^{n-2}=\sum\limits_{k=0}^{\infty}\frac{1}{(k+2)!}z^{k}=\sum\limits_{k=0}^{\infty}\frac{1}{k!(k+1)(k+1)}z^{k}</math> | ||
| + | azaz | ||
| + | :<math>f^{(k)}(0)=\frac{1}{(k+1)(k+2)}</math> | ||
<math> \scriptstyle{z_0\in\overline{\mathbf{C}}}</math> | <math> \scriptstyle{z_0\in\overline{\mathbf{C}}}</math> | ||
A lap 2008. december 1., 17:26-kori változata
Tartalomjegyzék |
Taylor-sor
A Cauchy-féle integrálformula következménye a következő tétel, mely a komplex differenciálelmélet egyik megjellegzetesebb eredménye:
Tétel. Ha az f: C 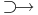 C függvény az értelmezési tartománya egy z0 pontjában és ennek egy nyílt környezetében komplex differenciálható (azaz z0-ban reguláris), akkor f a z0 pont egy V = Bδ(z0) környezetén mindenhol végtelenszer differenciálható, V minden pontjában az f z0-beli Taylor-sora konvergens és ennek határfüggvénye V-n előállítja f-et:
C függvény az értelmezési tartománya egy z0 pontjában és ennek egy nyílt környezetében komplex differenciálható (azaz z0-ban reguláris), akkor f a z0 pont egy V = Bδ(z0) környezetén mindenhol végtelenszer differenciálható, V minden pontjában az f z0-beli Taylor-sora konvergens és ennek határfüggvénye V-n előállítja f-et:
(azaz f analitikus z0-ban).
A tétel tehét azt mondja ki, hogy "reguláris függvény analitikus".
Megjegyezzük, hogy 1. mint minden nemnegatív egész hatványokat tartalmazó hatványsor, a Taylor-sor is egy körlap belsején abszolút konvergens, mely körlap sugara a konvergenciasugára, mely
ahol a sor a ∑an(z-z0)n, a körlap középpontja z0, és ahol a reciprok kivételesen úgy értendő, hogy 1/0 = ∞, 1/∞ = 0.
2. A legyakrabban használt Taylor-sorok a következők:
természetesen az utolsónál a z=1 pont 1 sugarú nyílt környezetében értelmezett logaritmusról van szó.
3. Mint minden hatványsor ez is egyenletesen konvergál az összegfüggvényéhez, így tagonként deriválható és integrálható.
Laurent-sor
A következőkben olyan függvényekkel foglalkozunk, melyek egy adott pontban nem feltétlenül regulárisak, de azon kívül egy környzetben azok.
Tétel. Ha az f: C 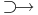 C függvény olyan, hogy a z0 pont egy
C függvény olyan, hogy a z0 pont egy 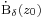 kipontozott környezetében az f függvény reguláris, akkor a z0 pont körül f Laurent-sorba fejthető, azaz léteznek olyan z_0 körüli
kipontozott környezetében az f függvény reguláris, akkor a z0 pont körül f Laurent-sorba fejthető, azaz léteznek olyan z_0 körüli
körgyűrű hogy ezen belül egy
sor előállítja f-et.
A körgyűrű sugarai
Reguláris- és főrész
A Laurent-sor
részét a sor főrészének, a
részét a sor reguláris részének nevezzük.
A Laurent-sor együtthatói
amennyiben a G egy a körgyűrűben haladó a z0-t egyszer körülölelő zárt görbe.
Főrész nélküli Laurent-sor
Ha nincs a Laurent-sornak főrésze, akkor R-=0 és az f függvény a z0 pontban vagy reguláris, vagy megszüntethető szakadása van. Ez utóbbi amiatt, hogy ebben az esetben f a z0-on kívül azonos egy hatványsor összegfüggvényével, mely azonban Abel tétele miatt folytonos és így határértéke a helyettesítési értékkel egyenlő. Tehát, ha f ilyen, akkor:
hiszen a hatványsoroknál a középpontban a 00 hatványt 1-nek értelmezzük.
f kiterjeszthető ezek szerint analitikusan kiterjeszthető és az értéke
Világos, hogy ezesetben a cn együtthatók pontosan az f kiterjesztésének Taylor-sori együtthatói, hiszen a deriváltakra vonatkozó Cauchy-formulákat a Taylor-sorral összevetve:
bármilyen a z0-t egyszer körülölelő, a körgyűrűben haladó zárt görbére.
Példa. Igazoljuk, hogy az alábbi függvény reguláris a 0 pontban és számítsuk ki a a kiterjesztés összes magasabbrendű deriváltját!
Megoldás. Elvileg ez egy Laurent-sor, hisz számlálóbeli reguláris függvény van elosztva z2-tel. De konkrétan elvégezve:
azaz f a 0-t kivéve egy reguláris függvénnyel egyenlő, azaz kiterjeszthető regulárissá és ez a fenti. A deriváltakat a Taylor-sor együtthatói adják a megfelelő faktoriálissal megsorozva. k=n-2-re:
azaz
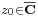
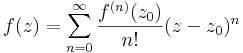
![R=\frac{1}{\limsup\limits_{n}\sqrt[n]{|a_n|}}\,](/upload/math/c/d/5/cd5d9fa4a84a6fe41527819693d07b1c.png)
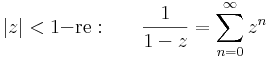
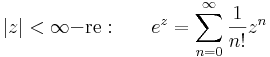
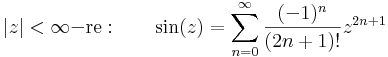
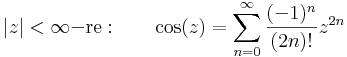
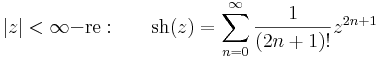
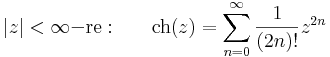
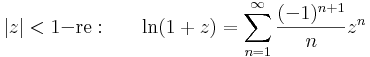
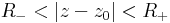
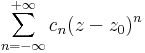
![R_+=\frac{1}{\limsup\limits_{n>0}\sqrt[n]{|c_n|}}\,](/upload/math/3/e/8/3e85834acf8b35a315b5d1921e8cb1f6.png)
![R_-=\limsup\limits_{n<0}\sqrt[n]{|c_n|}\,](/upload/math/c/f/7/cf758993102d05ada875ba223e7128d4.png)