|
|
| 175. sor: |
175. sor: |
| | :<math>3x^3\mathrm{ln}\,c|x|=y^3</math> | | :<math>3x^3\mathrm{ln}\,c|x|=y^3</math> |
| | :<math>x\sqrt[3]{3\,\mathrm{ln}\,c|x|}=y(x)\,</math> | | :<math>x\sqrt[3]{3\,\mathrm{ln}\,c|x|}=y(x)\,</math> |
| − |
| |
| − |
| |
| − | ==Feladat folytonosságra==
| |
| − | '''Feladat.''' Folytonos-e a ''z'' = i-ben az
| |
| − | :<math>f(z)=\left\{
| |
| − | \begin{matrix}
| |
| − | \cfrac{\mathrm{i}z+1}{|z-\mathrm{i}|},\quad\quad\mathrm{ha}\;z\ne \mathrm{i}\\
| |
| − | \\
| |
| − | 0,\quad\quad \mathrm{ha}\;z=\mathrm{i}
| |
| − | \end{matrix}
| |
| − | \right.</math>
| |
| − |
| |
| − | Ha ''z'' = ''x'' + i''y'' és (''x'',''y'') ≠ (0,1), akkor:
| |
| − | :<math>f(x,y)=\begin{pmatrix}
| |
| − | \cfrac{-y+1}{\sqrt{x^2+(y-1)^2}} \\
| |
| − | \cfrac{x}{\sqrt{x^2+(y-1)^2}}
| |
| − | \end{pmatrix}</math>
| |
| − |
| |
| − | Már az első komponens határértéke sem létezik, hisz (x,y)=(0,y) mentén alulról a (0,1)-hez tartva a határérték -1, az x=y-1 mentén pedig -1/gyök kettő.
| |
| − |
| |
| − | A második tényező szintén nem.
| |
| − |
| |
| − | =='''C''' kompaktifikálása==
| |
| − | ''Kompakt'' egy ''K'' halmaz, ha teljesül rá, hogy akárhogy is fedjük le nyílt halmazok rendszerével, azok közül már véges sok halmaz is lefedi a ''K''-t. Szimbolikusan:
| |
| − | :''K'' kompakt, ha minden (Ω<sub>i</sub>)<sub>i∈I</sub> halmazrendszerhez, melyre
| |
| − | :# Ω<sub>i</sub> nyílt minden i∈I-re és
| |
| − | :# ''K'' ⊆ U(Ω<sub>i</sub>)<sub>i∈I</sub>
| |
| − | :létezik J ⊆ I véges indexhalmaz, hogy ''K'' ⊆ U(Ω<sub>i</sub>)<sub>i∈J</sub>
| |
| − | '''R'''<sup>N</sup>-ben egy halmaz pontosan akkor kompakt, ha korlátos és zárt. Tehát maga '''C''' nem kompakt, hisz nem korlátos (bár zárt). Viszont '''C''' egyetlen egy ponttal kibővítve már kompakttá tehető, ugyanis egy ideális pont hozzávételével '''C''' kölcsönösen egyértelmű és folytonos kapcsolatba hozható a gömbfelülettel, mely '''R'''<sup>3</sup>-ban kompakt. Ezt a sztereografikus projekcióval oldjuk meg.
| |
| − |
| |
| − |
| |
| − | A Riemann-gömb konstrukciójához vegyük az '''R'''<sup>3</sup>-ban az origó középponttú egységgömböt és gondoljunk úgy az <nowiki>[xy]</nowiki> síkra, mint a '''C''' komplex számsíkra. Az egységgömb pontjait a következő módon feleltetjük meg a komplex számoknak. Tekintsük a gömbön a (0,0,1) koordinátájú ''P'' pólust és egy ''a'' + ''b''i komplex szám esetén az (''a'',''b'',0) pontot kössük össze ''P''-vel egy ''e'' egyenes által. Ekkor az ''e'' egyetlen pontban metszi az egységgömböt, mely kijelöli az ''a'' + ''b''i-nek megfelelő pontot. Ha az ''a'' + ''b''i-nek megfeleltetett Riemann-gömbfelületbeli pont koordinátái (x,y,z), akkor ezek kapcsolata:
| |
| − | :<math>a+b\mathrm{i}=\frac{x+\mathrm{i}y}{1-z}\,</math>
| |
| − |
| |
| − | '''Megjegyzés.''' Ismerős geometriai leképezésre bukkanhatunk, ha a Riemann-gömbfelület egy (x,y,h) és (x,y,-h) pontjának megfelelő komplex számnak a kapcsolatát írjuk fel. Legyen ugyanis
| |
| − | :<math>z=\frac{x+\mathrm{i}y}{1-h}\,</math> és <math>w=\frac{x+\mathrm{i}y}{1+h}\,</math>
| |
| − | Ekkor a ''z'' konjugáltját a ''w''-vel összeszorozva azt kapjuk, hogy:
| |
| − | :<math>w\cdot \overline{z}=1\,</math>
| |
| − | Amiből az következik, hogy a végpontok origótól vett távolságának a szorzata 1, azaz 1 a két szám hosszának mértani közepe. Ez viszont azt jelenti, hogy ''w'' nem más, mint a ''z'' ''inverziója'' az egységkörre vonakozóan és az inverziót kifejező komplex függvény a
| |
| − | :<math>w=\frac{1}{\,\overline{z}\,}\,</math>
| |
| − | leképezés.
| |
| − | Eszerint a reciprok-konjugált (de a reciprok is) egy origón át nem menő kört körbe, az origón átmenő kört egyenesbe, egy origón át nem haladó egyenes egy origón átmenő körbe és egy origón áthaladó egyenest saját magába képezi.
| |
| − |
| |
| − |
| |
| − | Ha tehát a '''C'''-hez hozzáveszünk egy ∞-nel jelölt objektumot, és ennek megfeleltetjük a ''P'' pólust, akkor a
| |
| − | :<math>\overline{\mathbf{C}}=\mathbf{C}\cup\{\infty\}\,</math>
| |
| − | halmaz kölcsönösen egyértelmű megfeleltetésbe hozható a Riemann-gömbfelülettel. Ahhoz, hogy ennek folytonosságáról beszélhessünk, definiálnunk kell ∞ gömbi környezeteit.
| |
| − | Ezek a következő alakú halmazok lesznek:
| |
| − | :<math>\mathrm{B}_r(\infty)=\left\{z\in \mathbf{C}: |z|>\frac{1}{r}\right\}\cup\{\infty\}\,</math>
| |
| − | ahol ''r'' > 0.
| |
| − |
| |
| − | '''Feladat.''' Igazoljuk, hogy '''C'''U{∞} ''kompakt''!
| |
| − |
| |
| − | ''(Útmutatás: az elsőhöz az origó körüli zárt gömbök kompaktságát, a másodikhoz a Bolzano-Weierstrass-féle kiválasztási tételt kell használni (persze korlátos sorozatra).)''
| |
| − |
| |
| − | Ha '''C'''U{∞}-t lefedi egy nyílt halmazrendszer, akkor ∞-t is lefedi belőlük egy, mondjuk ''U''. ''U'' lefedi az ∞ egy gömbi környezetét, mondjuk B<sub>r</sub>(∞)-t. Elegendő tehát tekintenünk '''C'''U{∞} lefedéséhez a halmazrendszerből az ''U''-t és a B<sub>r</sub>(∞) komplementerét lefedő halmazokat. De ez utóbbiakból véges sok is van melyek még mindig lefedik, mert B<sub>r</sub>(∞) komplemetere a 0 középponttú 1/r sugarú zárt körlap, mely kompakt.
| |
| − |
| |
| − | ==Határérték==
| |
| − | Komplex függvény '''C'''-beli pontban vett '''C'''-beli határértéke ugyanúgy értelmezett, mint az '''R'''<sup>2</sup> esetben. Itt is érvényes, hogy pontosan akkor látezik a határérték, ha a komponensfüggvényeknek létezik a határértéke és ekkor a határérték egyenlő lesz a valós és képzetes komponens határértékéből alkotott komplex számmal.
| |
| − |
| |
| − | A ∞ miatt érdemes külön is megfogalmazni a határérték definícióját, bár az teljesen analóg a valós esettel. Legyen ''f'' egy az ''A'' ⊆ '''C''' halmazon értelmezett, '''C'''-be képező függvény. Legyen <math>\scriptstyle{u\in \overline{\mathbf{C}}}</math> az ''A'' torlódási pontja, azaz minden ''r'' > 0 esetén legyen olyan ''a'' ∈ ''A'', hogy ''a'' ∈ B<sub>r</sub>(''u'')\{u}. Azt mondjuk, hogy az ''f''-nek a <math>\scriptstyle{v\in \overline{\mathbf{C}}}</math> elem határértéke az ''u''-ban, ha
| |
| − | :minden ε > 0 esetén létezik olyan δ > 0, hogy minden ''z'' ∈ ''A'' ∩ B<sub>δ</sub>(''u'')\{u}-re ''f''(''z'') ∈ B<sub>ε</sub>(''v'')
| |
| − |
| |
| − | ahol természetesen a ∞ környezetei a már említett módon értendők.
| |
| − |
| |
| − | '''Feladat.''' Igazoljuk definíció szerint, hogy
| |
| − | #<math>\lim\limits_{z\to 0}\frac{1}{z}=\infty</math>
| |
| − | #<math>\lim\limits_{z\to \infty}\frac{1}{z}=0</math>
| |
| − |
| |
| − | 1. Legyen ε > 0. Ekkor azt kell belátnuk, hogy létezik δ > 0, hogy teljesüljön |''z''| < δ esetén, hogy a függvényérték a ∞ ε sugarú környezetébe esik, azaz:
| |
| − | :<math>\left|\frac{1}{z}\right|>\frac{1}{\varepsilon}</math>
| |
| − | Világos, hogy ezt azt jelenti, hogy
| |
| − | :<math>|z|<\varepsilon</math>
| |
| − | amit reciprokvonással kaptunk. Ha tehát ha δ := ε és |''z''| < δ, akkor "felfelé" következtetve kijön a kívánt egyenlőtlenség.
| |
| − |
| |
| − | 2. Legyen ε > 0. Ekkor azt kell belátnuk, hogy létezik δ > 0, hogy teljesüljön |''z''| > 1/δ esetén, hogy a függvényérték a 0-nak ε sugarú környezetébe esik, azaz:
| |
| − | :<math>\left|\frac{1}{z}\right|<\varepsilon</math>
| |
| − | Világos, hogy ezt azt jelenti, hogy
| |
| − | :<math>|z|>\frac{1}{\varepsilon}</math>
| |
| − | amit reciprokvonással kaptunk. Ha tehát ha δ := ε és |''z''| > 1/δ, akkor "felfelé" következtetve kijön a kívánt egyenlőtlenség.
| |
| − |
| |
| − | A végtelen határérékkel történő számolás szabályai előtt definiálnunk kell néhány kibővített műveletet. Ezt a következők szellemében tesszük:
| |
| − |
| |
| − | :Ha ''a'' és ''b'' valamelyike a ∞ szimbólum (a másik, ha nem ilyen, akkor komplex szám), akkor az ''a'' * ''b'' alapműveletet akkor értelmezzük a ''c'' szimbólumként (mely szintén vagy komplex szám, vagy az ∞), ha ''minden'' ''a'' határértékű ''f'' függvény esetén és ''minden'' ''b'' határértékű ''g'' függvény esetén a ''f''*''g'' ''szükségszerűen'' a ''c''-hez tart. Ekkor mondjuk tehát, hogy az
| |
| − | ::''a'' * ''b'' = ''c''
| |
| − | :definíció jó.
| |
| − | Például a ∞ + ∞ művelet feltétlenül értelmezett és értéke a ∞, mert könnyen látható, hogy ''bármely'' két, a ∞-hez tartó függvény összege is a ∞-hez tart. De a 0 <math>\cdot</math> ∞ művelet nem értelmezhető, mert van két függvénypár, mely ilyen alakú határértékekkel rendelkezik, de a szorzatuk máshoz tart. Pl.: (1/Re(z)) <math>\cdot</math> Re(z) <math>\to</math> 1, a z=0-ban, de (1/Re(z)) <math>\cdot</math> 2 Re(z) <math>\to</math> 2 a z=0-ban.
| |
| − |
| |
| − | '''Definíció''' – ''Végtelen és alapműveletek'' – Az alábbi műveleti szabályokat vezetjük be a ∞, szimbólumra vonatkozóan, az alábbiakban ''z'' tetszőleges komplex szám, ''n'' tetszőleges nemnulla komplex szám:
| |
| − | # <math>\infty+z=\infty </math>,
| |
| − | # <math>\infty-z=\infty, \quad\quad z-\infty=\infty</math>,
| |
| − | # <math>\infty\cdot\infty=\infty, \quad\quad \infty\cdot n=\infty</math>,
| |
| − | # <math>\frac{z}{\infty}=0 \quad\quad \frac{\infty}{z}=\infty</math>,
| |
| − | továbbá a szorzás és az összeadás kommutatív.
| |
| − |
| |
| − | Megjegyezzük még, hogy <math>\overline{\infty}=\infty</math>, azaz a végtelen konjugáltja saját maga.
| |
| − |
| |
| − | '''Definíció''' – ''Határozatlan esetek'' – Az alábbi alapműveletek nem értelmezhetők:
| |
| − | # <math>\infty-\infty</math>,
| |
| − | # <math>0\cdot\infty, \quad\quad \infty\cdot 0</math>,
| |
| − | # <math>\frac{\infty}{\infty}</math>,
| |
| − | # <math>\frac{0}{0}</math>
| |
| − |
| |
| − |
| |
| − | '''Tétel''' – ''Végtelen határérték és alapműveletek'' – Ha az ''f'' és ''g'' komplex függvényeknek létezik határértékük az <math>\scriptstyle{u\in \overline{\mathbf{C}}}</math> helyen, az ''f'' * ''g'' alapművelettl elkészített függvény értelmezési tartományának torlódási pontja ''u'' és a lim<sub>u</sub> ''f'' * lim<sub>u</sub> ''g'' alapművelet elvégezhető, akkor az ''f'' * ''g'' függvénynek is van határértéke ''u''-ban és ez:
| |
| − | :<math> \lim\limits_u(f\mbox{*}g)=\lim\limits_u f\,\mbox{*}\, \lim\limits_u g \,</math>
| |
| − | Ezenkívül a határozatlan esetekben, amikor a határértékekkel végzett műveletek nem értelmezettek, az alapműveletekkel elkészített függvények határértékeire nem adható általános képlet (mert alkalmasan választott esetekben máshoz és máshoz tartanak).
| |
| − |
| |
| − | ''A bizonyításról.'' Ennek a tételnek a bizonyítása minden nehézség nélkül elvégezhető vagy az '''R'''<sup>2</sup>-beli sorozatokra vonatkozó átviteli elv vagy a komponensfüggvények határértékére történő hivatkozás útján. Minenekelőtt azt kell szem előtt tartanunk, hogy a végtelenhez való tartás, a függvény abszolútértékének plusz végtelenhez tartását jelenti:
| |
| − | :<math>\exists\lim\limits_{z_0}f=\infty \quad\Longleftrightarrow \quad\exists\lim\limits_{z_0}|f|=+\infty</math>
| |
| − |
| |
| − | '''Feladat.''' Adjuk példákat arra, hogy a határozatlan alakú határértékeket valóban nem lehet definiálni.
| |
| − |
| |
| − | ''Nézzük a 0-ban az alábbi függvényeket:''
| |
| − | :<math>\frac{2}{z}\;-\;\frac{1}{z}=\frac{1}{z}\quad\to \infty</math> miközben <math>(\frac{1}{z}+2)\;-\;\frac{1}{z}=2\quad\to 2</math>
| |
| − |
| |
| − | <math>\frac{1}{z}\;\cdot z=1\quad\to 1</math> miközben <math>\frac{2}{z}\;\cdot\;z=2\quad\to 2</math>
| |
| − |
| |
| − | :<math>\frac{1}{z}/\frac{1}{z}=1\quad\to 1</math> miközben <math>\frac{2}{z}/\frac{1}{z}=2\quad\to 2</math>
| |
| − |
| |
| − | <math>\frac{z}{z}=1\quad\to 1</math> miközben <math>\frac{2z}{z}=2\quad\to 2</math>
| |
| − |
| |
| − | '''Feladat.''' Számítsuk ki az alábbi határértékeket, ha léteznek!
| |
| − | # <math>\lim\limits_{z\to 0}\frac{\mathrm{Im}(z)}{z}</math>,
| |
| − | # <math>\lim\limits_{z\to i}\frac{z-i}{z^2+1}</math>,
| |
| − | # <math>\lim\limits_{z\to 1}\frac{\frac{1}{z-1}+i}{\frac{1}{z^2-1}-i}</math>,
| |
| − | # <math>\lim\limits_{z\to 0}\frac{1}{z}-\frac{2}{\overline{z}}</math>,
| |
| − | # <math>\lim\limits_{z\to -i}\frac{\frac{1}{z+i}+i}{\overline{z}-i}</math>,
| |
| − |
| |
| − | ''Megoldás.''
| |
| − | 1. nemnulla ''z''-re:
| |
| − | :<math>\frac{\mathrm{Im}(z)}{z}=\frac{\mathrm{Im}(z)\overline{z}}{z\overline{z}}=\frac{yx-y^2\mathrm{i}}{x^2+y^2}</math>
| |
| − | de ekkor például az első komponensfüggvény ''x'' = 0 felől közelítve 0, míg az ''x'' = ''y''-felől:1/2, azaz nem létezik az első komponensnek a (0,0)-ban határértéke, azaz a komplex függvénynek sem.
| |
| − |
| |
| − | 2. <math>\frac{z-i}{z^2+1}=\frac{z-i}{(z+i)(z-i)}=\frac{1}{z+i}\quad\longrightarrow_{z\to i}\quad\infty</math>
| |
| − |
| |
| − | 3. <math>\frac{\frac{1}{z-1}+i}{\frac{1}{z^2-1}-i}=\frac{ \frac{1+iz-i}{z-1} }{ \frac{1-iz^2+i}{z^2-1} }=\frac{1+iz-i}{z-1}\cdot \frac{(z+1)(z-1)}{1-iz^2+i}</math>
| |
| − | ::<math>\left.\frac{iz+1-i}{-iz^2+i+1}(z+1)\right|_1=\frac{1}{1}\cdot 1</math>
| |
| − |
| |
| − | 4. <math>\frac{1}{z}-\frac{2}{\overline{z}}=\frac{\overline{z}-2z}{z\overline{z}}</math>
| |
| − | csak a valós részt nézve:
| |
| − | :<math>\left|\frac{-x}{x^2+y^2}\right|</math>
| |
| − | az (x,y)=(x,0) esetben a (0,0)-hoz tartva: végtelen, de (x,y)=(0,y), akkor 0. tehát nincs határérték.
| |
| − |
| |
| − | 5. <math>\lim\limits_{z\to -i}\frac{\frac{1}{z+i}+i}{\overline{z}-i}=\left(\frac{\infty}{0}\right)=\infty</math>.
| |
| − |
| |
| − |
| |
| − | '''Feladat.''' Adjuk meg minden ''z''<sub>0</sub> ∈ '''C''' számra az alábbi függvény határértékét!
| |
| − | # <math>f(z)=\frac{z}{\overline{z}-z}</math>,
| |
| − | # <math>f(z)=\frac{z^2}{\overline{z}z-1}</math>,
| |
| − |
| |
| − | 1. <math>\mathrm{Dom}(f)=\{z\in \mathbf{C}\mid \overline{z}\ne z\}</math>
| |
| − |
| |
| − | Folytonos az értelmezési tartományában. A határon:
| |
| − | :<math>\frac{z}{\overline{z}-z}=\frac{x+iy}{2iy}\,</math>
| |
| − | ''z''<sub>0</sub> ≠ 0 esetén
| |
| − | :<math>\left|\frac{x+iy}{2iy}\right|\geq \frac{|z_0|/2}{2|y|}\to \infty</math>
| |
| − | ''z''<sub>0</sub> = 0 esetén:
| |
| − | :<math>\frac{x+iy}{2iy}=\frac{1}{2}-i\frac{x}{2y}</math>
| |
| − | ismert, hogy nincs határérték.
| |
| − |
| |
| − | 2. <math>\mathrm{Dom}(f)=\{z\in \mathbf{C}\mid \overline{z}z\ne 1\}</math>
| |
| − |
| |
| − | Az egységkör pontjaitól különbözőkre folytonos, az egységkörön a végtelen, a végtelenben pedig nincs határérték. Ugyanis:
| |
| − | :<math>|f(z)|=\frac{|z|^2}{|\overline{z}z-1|}</math>,
| |
| − | így az egységkörön a számláló az 1-hez, a nevező a nullához tart. A végtelenben pedig ''t'' valóssal:
| |
| − | :<math>\lim\limits_{t\to +\infty} f(t+0.i)=\lim\limits_{t\to +\infty} \frac{t^2}{t^2-1}= 1\,</math>
| |
| − | :<math>\lim\limits_{t\to +\infty} f(t.i)=\lim\limits_{t\to +\infty} \frac{-t^2}{t^2-1}= -1\,</math>
| |
Jelen esetben a G függvény deriváltja (G'=g) sehol sem nulla folytonos függvény, ezért szigorúan monoton. Emiatt kifejezhető y éspedig:
egyenlet. Mivel
ezért az implicitfüggvény-tétel miatt, hogy y-t "ki lehet fejezni". Érdemes felelevenítenünk magát az implicitfüggvény-tételt:
így az implicitfüggvény-tétel szerint, egyértelműen létezik F-nek y=y(x) implicit függvénye az adott pont egy környezetében és ennek deriváltja az értelmezési tartományának minden pontjában:
alakban. Most belátjuk, hogy y (impl)-nek implicit megoldása. Az összetett függvény differenciálási szabálya miatt ( d(F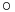 G)(x,y)=dF(G(x,y))
G)(x,y)=dF(G(x,y))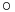 dG(x,y) ) az előző egyenlet a következő formában is írható:
dG(x,y) ) az előző egyenlet a következő formában is írható:
2) Az implicitfüggvény tételében adott egyetlen implicit függvény az 1) egzisztencia része miatt megoldása (ex)-nek és 1) unicitás része miatt ez az egyetlen megoldása (ex)-nek.
alakban is szokás írni.
Ezt a mai jelölésekkel a következőképpen írjuk. Egy F kétváltozós függvény teljes differenciálja egy lineáris leképezés, mely a sztenderd {(1,0),(0,1)} bázisban felírt koordinátáival nem más, mit a parciális deriváltjainak sormátrixa:
Az F függvényt, az Pdx + Qdy = 0 egyenlet integráljának nevezzük.
Ezt a tételt jól ismerjük és a bizonyítását a vektoranalízisben vettük.
2) Bár a szeparábilis egyenlet egzakt, a fenti feltétel az egzaktság ellenőrzésére sokkal szigorúbb mint a szeparábilis egyenlet megoldhatóságának feltétele.
Tehát egzakt. Az egyenlet első integrálját megkapjuk, ha megoldjuk az
parciális differenciálegyenlet-rendszert.
Általában egy P(x,y)dx+Q(x,y)dy=0 alakú differenciálegyenlet esetén nem teljesül a rot(P,Q)=0 feltétel. Esetenként azonban található olyan μ kétváltozós pozitív értékű függvény, amellyel:
már egzakt egyenlet. Vizsáljuk meg miből nyerhetjük az ilyen μ un. integráló szorzót! A rot(μP,μQ)=0 feltétel a következő:
Ezt a parciális differenciálegyenletet kell megoldanunk ahhoz, hogy legyen integráló tényezőnk.
alakban a keresztben vett deriváltak: 0 és f(x).
Q=1 és P(x,y)=-g(x)+f(x)y ezért a μ-t adó parc.diff. egyenlet:
Elegendő egy partikuláris megoldást találni, amit egyszerűen megkapunk, ha csak az olyan μ-ket keressük, amik csak az x-től függenek, ekkor ugyanis pl. g(x) nem is lesz az egyenletben. Ilyet találunk, mert:
ahol F'=f.
Tanulságképpen megállapíthatjuk, hogy néha érdemes a μ-re felírt egyenletnek csak olyan megoldásait keresni, amelyek csak az egyik változótól függenek. Ha ugyanis csak a μ=μ(x) alakú integráló szorzókra szorítkozunk, akkor a megoldandó egyenlet:
csak x-től függjön (vagy a -rot(P,Q)/P csak y-tól és akkor μ csak y-tól függ).
azaz célravezet, ha μ-t μ(x) alakban keressük. Ekkor
 R folytonos függvények, Q sehol sem nulla. Azt mondjuk, hogy az
R folytonos függvények, Q sehol sem nulla. Azt mondjuk, hogy az
 R folytonosan differenciálható függvény, hogy
R folytonosan differenciálható függvény, hogy
 R folytonosan differenciálható függvény az (x0,y0) ∈ int(I×J) pontban teljesíti a ∂Φ/∂y ≠ 0 feltételt és Φ(x0,y0)=0, akkor a Φ(x,y)=0 egyenletnek van az (x0,y0) ponton áthaladó implicit függvénye és ennek deriváltja:
R folytonosan differenciálható függvény az (x0,y0) ∈ int(I×J) pontban teljesíti a ∂Φ/∂y ≠ 0 feltételt és Φ(x0,y0)=0, akkor a Φ(x,y)=0 egyenletnek van az (x0,y0) ponton áthaladó implicit függvénye és ennek deriváltja:
 R folytonosan differenciálható függvénnyel és (x0,y0) ∈ U. Ekkor
R folytonosan differenciálható függvénnyel és (x0,y0) ∈ U. Ekkor
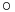 G)(x,y)=dF(G(x,y))
G)(x,y)=dF(G(x,y))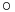 dG(x,y) ) az előző egyenlet a következő formában is írható:
dG(x,y) ) az előző egyenlet a következő formában is írható:
 F(x,y(x)) egy konstans függvény. De a feltétel szerint y(x0) = y0 teljesül, ezért x
F(x,y(x)) egy konstans függvény. De a feltétel szerint y(x0) = y0 teljesül, ezért x  y(x) egy (x0,y0)-on áthaladó implicit függvénye az F(x,y)=F(x0,y0) egyenletnek. Ez az utóbbi azonban egyértelműen van meghatározva, ezért a kezdeti érték feladat minden megoldása egybeesik ezzel az implicit függvénnyel, azaz a megoldás egyértelmű.
y(x) egy (x0,y0)-on áthaladó implicit függvénye az F(x,y)=F(x0,y0) egyenletnek. Ez az utóbbi azonban egyértelműen van meghatározva, ezért a kezdeti érték feladat minden megoldása egybeesik ezzel az implicit függvénnyel, azaz a megoldás egyértelmű.
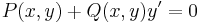 ill.
ill. 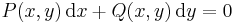
![[\mathrm{d}F]=\left[P,Q\right]\,](/upload/math/3/4/3/343e00846494e553e629c9e57344a211.png) ill.
ill. ![\mathrm{grad}\,F=[P,Q]\,](/upload/math/4/f/9/4f9b9ba5601098c77e15e1f242d50948.png)
 R folytonosan differenciálható függvények (Q sehol sem nulla). A Pdx + Qdy = 0 egyenlet pontosan akkor egzakt, ha
R folytonosan differenciálható függvények (Q sehol sem nulla). A Pdx + Qdy = 0 egyenlet pontosan akkor egzakt, ha
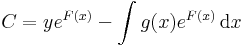
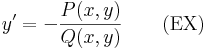
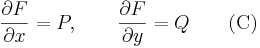
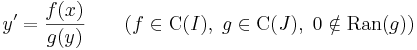
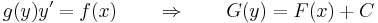
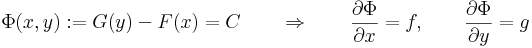
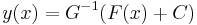
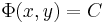
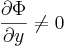
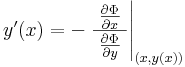
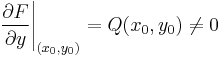
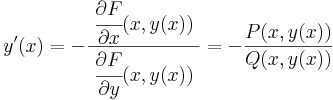
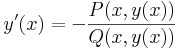
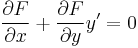
![(F(x,y(x)))'=[\mathrm{grad}\,F|_{(x,y(x))}]\cdot\begin{bmatrix}x'\\y'(x)\end{bmatrix}=\frac{\partial F}{\partial x}|_{(x,y(x))}+y'\frac{\partial F}{\partial y}|_{(x,y(x))}\equiv 0\,](/upload/math/6/a/0/6a01c3a741e5c2d447b6e0254117aa36.png)
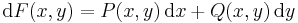
![[\mathrm{d}F(x,y)]=\mathrm{grad}\,F(x,y)=\left[\;\frac{\partial F}{\partial x}\;,\;\frac{\partial F}{\partial y}\;\right]](/upload/math/6/d/6/6d677f005d45feb13decbeb9f8433c81.png)
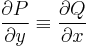
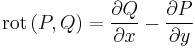
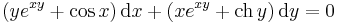
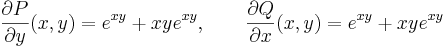
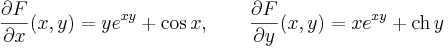
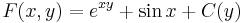
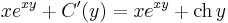
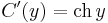
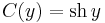
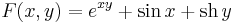
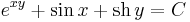
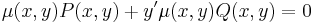
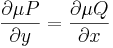
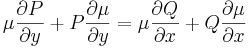
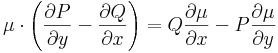
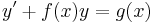
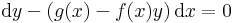
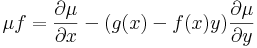
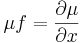
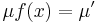
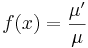
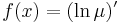
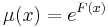
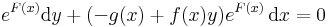
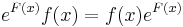
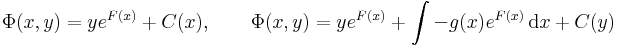
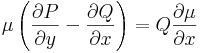
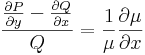
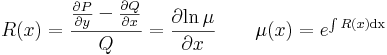
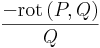
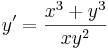
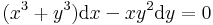
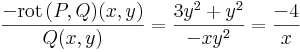
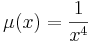
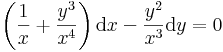
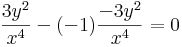
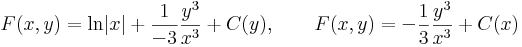
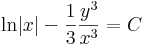
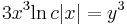
![x\sqrt[3]{3\,\mathrm{ln}\,c|x|}=y(x)\,](/upload/math/d/d/0/dd047c99fd5100a705896f6427be4de3.png)