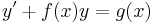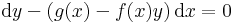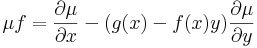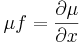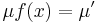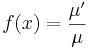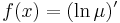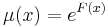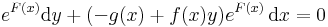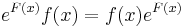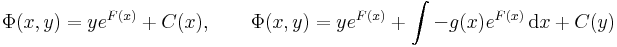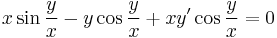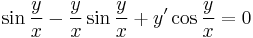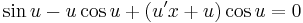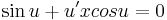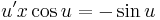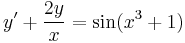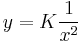Matematika A3a 2008/3. gyakorlat
Mozo (vitalap | szerkesztései) (→Kritériumok az abszolút konvergenciára) |
Mozo (vitalap | szerkesztései) (→Speciális esetek) |
||
| (egy szerkesztő 30 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
''<sub><[[Matematika A3a 2008]]</sub>'' | ''<sub><[[Matematika A3a 2008]]</sub>'' | ||
| − | == | + | ==Integráló tényező== |
| − | + | Általában egy P(x,y)dx+Q(x,y)dy=0 alakú differenciálegyenlet esetén nem teljesül a rot(P,Q)=0 feltétel. Esetenként azonban található olyan μ kétváltozós pozitív értékű függvény, amellyel: | |
| − | :<math> | + | :<math>\mu(x,y) P(x,y)+y'\mu(x,y) Q(x,y)=0\,</math> |
| − | \ | + | már egzakt egyenlet. Vizsáljuk meg miből nyerhetjük az ilyen μ un. '''integráló szorzót'''! A rot(μP,μQ)=0 feltétel a következő: |
| − | + | :<math>\frac{\partial\mu P}{\partial y}=\frac{\partial\mu Q}{\partial x}\,</math> | |
| − | \\ | + | :<math>\mu\frac{\partial P}{\partial y}+P\frac{\partial\mu }{\partial y}=\mu\frac{\partial Q}{\partial x}+Q\frac{\partial \mu}{\partial x}\,</math> |
| − | \ | + | :<math>\mu\cdot\left(\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}\right)=Q\frac{\partial \mu}{\partial x}-P\frac{\partial\mu }{\partial y}\,</math> |
| − | \\ | + | Mivel |
| − | \ | + | :<math>\frac{1}{\mu}\frac{\partial \mu}{\partial x}=\frac{\partial \ln\mu }{\partial x}</math> |
| − | \ | + | és ugyanígy |
| − | + | :<math>\frac{1}{\mu}\frac{\partial \mu}{\partial y}=\frac{\partial \ln\mu }{\partial y}</math> | |
| + | ezért | ||
| + | :<math>\left(\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}\right)=Q\frac{\partial \ln\mu}{\partial x}-P\frac{\partial\ln\mu}{\partial y}\,</math> | ||
| + | Ezt a parciális differenciálegyenletet kell megoldanunk ahhoz, hogy legyen integráló tényezőnk. | ||
| − | + | ==Speciális esetek== | |
| + | Megállapíthatjuk, hogy néha érdemes a μ-re felírt egyenletnek csak olyan megoldásait keresni, amelyek csak az egyik változótól függenek. Ez a következő esekben áll elő. | ||
| − | + | I. Keressük a megoldást a μ=μ(x) feltevéssel! Ekkor ln(μ)=ln(μ)(x) és ∂<sub>y</sub>ln(μ)=0, azaz | |
| − | : | + | :<math>\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}=Q\frac{\partial \ln\mu}{\partial x}\,</math> |
| − | : | + | és |
| + | :<math>R(x)=\frac{\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}}{Q}=\frac{\partial \ln\mu}{\partial x}\,</math> | ||
| + | csak x-től függ és innen az integráló szorzó: | ||
| + | :<math>\mu(x)=e^{\int R(x)\;dx}</math> | ||
| − | |||
| − | + | '''Példa.''' | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | Az x>0, y tetszőleges kezdeti érték tarrtományban oldjuk meg az alábbi egyenletet! | |
| + | :<math>\,(x^2+y^2+x)dx+xydy=0</math>, <math>(xyy'=-x^2-y^2-x)</math> | ||
| + | '''Mo.''' <math>P=x^2+y^2+x</math>, <math>Q=xy</math>, <math>\partial_y P=2y</math>, <math>\partial_yQ=y</math> azaz nem egzakt, de | ||
| + | :<math>\frac{\partial_y P-\partial_yQ}{Q}=\frac{2y-y}{xy}=\frac{1}{x}=R(x)</math>, <math>\mu(x)=e^{\int\frac{1}{x}\mathrm{d}x}=x</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | II. Keressük a megoldást a μ=μ(y) feltevéssel! Ekkor ln(μ)=ln(μ)(y) és ∂<sub>x</sub>ln(μ)=0, azaz | ||
| + | :<math>\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}=-P\frac{\partial \ln\mu}{\partial y}\,</math> | ||
| + | és | ||
| + | :<math>S(y)=\frac{\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}}{P}=-\frac{\partial \ln\mu}{\partial y}\,</math> | ||
| + | csak y-től függ és innen az integráló szorzó: | ||
| + | :<math>\mu(y)=e^{-\int S(y)\;dy}</math> | ||
| − | + | '''Megj.:''' A gyakorlatban ilyenkor vesszük az | |
| + | :<math>\frac{\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}}{Q}</math> ill. <math>\frac{\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}}{P}</math> | ||
| + | törteket és ellenőrizzük, hogy rendre csak x-től vagy csak y-tól függenek. Ha valamelyik, akkor azt a megoldást választjuk. | ||
| − | + | '''Példa.''' | |
| − | + | Oldjuk meg az | |
| − | : <math> | + | :<math>-x^2\cos^4y\,\mathrm{d}x+\sin y\,\mathrm{d}y=0</math> |
| − | + | egyenletet! | |
| − | + | ||
| − | + | ||
| − | === | + | ''1. Mo.'' |
| + | Nem egzakt: | ||
| + | :<math>\frac{\partial P}{\partial y}=4x^2\cos^{3}y(\sin y)</math> | ||
| + | :<math>\frac{\partial Q}{\partial x}=0</math> | ||
| + | Egzakttá tehető, ugyanis: | ||
| + | :<math>-\frac{\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}}{P}=\frac{4x^2\cos^{3}y(\sin y)}{x^2\cos^4y}=\frac{4\sin y}{\cos y}</math> | ||
| + | :<math>\mu=e^{\int\frac{4\sin y}{\cos y}}=e^{-4 \mathrm{ln}|cos y |}=\frac{1}{\cos^4y}</math> | ||
| + | Emiatt | ||
| + | :<math>-x^2\,\mathrm{d}x+\frac{\sin y}{\cos^4 y}\,\mathrm{d}y=0</math> | ||
| + | Megoldása: | ||
| + | :<math>-\frac{x^3}{3}+\frac{1}{3\cos^3 y}\,=C</math> | ||
| + | ''2. Mo.'' | ||
| + | Szeparábilis is. | ||
| − | + | III. Előfordulhat, hogy szeparábilis alakban kell keresnünk a parc. diff. egyenlet megoldását, azaz μ(x,y)=φ(x)ψ(y) alakban. Ekkor -- mint az könnyen ellenőrizhető -- az egyenlet | |
| − | :<math>\ | + | :<math>\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}=Qf(x)-Pg(y)\,</math> |
| − | + | alakú és az integráló szorzó | |
| − | :<math>\ | + | :<math>\mu(x,y)=e^{\int f(x)\;dx+\int g(y)\;dy}</math> |
| − | + | ||
| − | = | + | '''Példa.''' Oldjuk meg az |
| + | :<math>y'=\frac{x^3+y^3}{xy^2}\,</math> | ||
| + | egyenletet! | ||
| − | + | ''Mo.'' Átrendezve: | |
| + | :<math>(x^3+y^3)\mathrm{d}x-xy^2\mathrm{d}y=0\,</math> | ||
| + | ∂<sub>y</sub>P=3y<sup>2</sup>, ∂<sub>x</sub>Q=-y<sup>2</sup>, | ||
| + | azaz | ||
| + | :<math>\frac{-\mathrm{rot}\,(P,Q)(x,y)}{Q(x,y)}=\frac{3y^2+y^2}{-xy^2}=\frac{-4}{x}</math> | ||
| + | azaz célravezet, ha μ-t μ(x) alakban keressük. Ekkor | ||
| + | :<math>\mu(x)=\frac{1}{x^4}</math> | ||
| + | Ekkor az egyenlet: | ||
| + | :<math>\left(\frac{1}{x}+\frac{y^3}{x^4}\right)\mathrm{d}x-\frac{y^2}{x^3}\mathrm{d}y=0\,</math> | ||
| + | egzakt, mert | ||
| + | :<math>\frac{3y^2}{x^4}-(-1)\frac{-3y^2}{x^4}=0\,</math> | ||
| + | Integrálássa: | ||
| + | :<math>F(x,y)=\mathrm{ln}|x|+\frac{1}{-3}\frac{y^3}{x^3}+C(y),\quad\quad F(x,y)=-\frac{1}{3}\frac{y^3}{x^3}+C(x)\,</math> | ||
| + | azaz | ||
| + | :<math>\mathrm{ln}|x|-\frac{1}{3}\frac{y^3}{x^3}=C</math> | ||
| + | :<math>3x^3\mathrm{ln}\,c|x|=y^3</math> | ||
| + | :<math>x\sqrt[3]{3\,\mathrm{ln}\,c|x|}=y(x)\,</math> | ||
| − | + | ==Elméleti példák== | |
| + | '''1.''' Az y'=-P/Q homogén fokszámú egyenlet, melyben P és Q azonos fokszámú homogén függvények szintén egzakttá tehető az 1/(Px+Qy) szorzóval, ha ez nem az y'=-y/x egyenlet (ennek meg ismerjük a megoldását). | ||
| + | |||
| + | '''2.''' Keressünk integráló tényezőt az | ||
| + | :<math>y'+f(x)y=g(x)\,</math> | ||
| + | közönséges elsőrendű inhomogén lineáris differenciálegyenlethez! | ||
| + | |||
| + | Világos, hogy nem egzakt, mert a | ||
| + | :<math>\mathrm{d}y-(g(x)-f(x)y)\,\mathrm{d}x=0</math> | ||
| + | alakban a keresztben vett deriváltak: 0 és f(x). | ||
| + | |||
| + | Q=1 és P(x,y)=-g(x)+f(x)y ezért a μ-t adó parc.diff. egyenlet: | ||
| + | :<math>\mu f=\frac{\partial \mu}{\partial x}-(g(x)-f(x)y)\frac{\partial\mu }{\partial y}\,</math> | ||
| + | Elegendő egy partikuláris megoldást találni, amit egyszerűen megkapunk, ha csak az olyan μ-ket keressük, amik csak az x-től függenek, ekkor ugyanis pl. g(x) nem is lesz az egyenletben. Ilyet találunk, mert: | ||
| + | :<math>\mu f=\frac{\partial \mu}{\partial x}\,</math> | ||
| + | :<math>\mu f(x)=\mu'\,</math> | ||
| + | Ez egy szeparábilis, aminek a megoldása: | ||
| + | :<math>f(x)=\frac{\mu'}{\mu}\,</math> | ||
| + | :<math>f(x)=(\mathrm{ln}\,\mu)'\,</math> | ||
| + | egy partikuláris megoldás: | ||
| + | :<math>\mu(x)=e^{F(x)}\,</math> | ||
| + | ahol F'=f. | ||
| + | |||
| + | '''HF''': Keressük meg ezzel az integáló szorzóval az általános megoldást! | ||
| + | |||
| + | ''Mo.'' | ||
| + | :<math>e^{F(x)}\mathrm{d}y+(-g(x)+f(x)y)e^{F(x)}\,\mathrm{d}x=0</math> | ||
| + | Már egzakt, hiszen | ||
| + | :<math>e^{F(x)}f(x)=f(x)e^{F(x)}\,</math> | ||
| + | Ekkor | ||
| + | :<math>\Phi(x,y)=ye^{F(x)}+C(x),\quad\quad \Phi(x,y)=ye^{F(x)}+\int -g(x)e^{F(x)}\,\mathrm{d}x+C(y)</math> | ||
| + | azaz | ||
| + | <math>C=ye^{F(x)}-\int g(x)e^{F(x)}\,\mathrm{d}x</math> | ||
| + | <center> | ||
| + | </center> | ||
| + | ==Gyakorlás== | ||
| + | |||
| + | Oldja meg az alábbi egyenletet az a) y(π)=0 ill. b) y(2/π)=1 kezdeti feltétel mellett! | ||
| + | :<math>x\sin\frac{y}{x}-y\cos\frac{y}{x}+xy'\cos\frac{y}{x}=0</math> | ||
| + | '''Mo.''' Legyen <math>u=y/x</math>, innen <math>y'=u'x+u</math> | ||
| + | :<math>\sin\frac{y}{x}-\frac{y}{x}\sin\frac{y}{x}+y'\cos\frac{y}{x}=0</math> | ||
| + | :<math>\,\sin u-u\cos u+(u'x+u)\cos u=0</math> | ||
| + | :<math>\,\sin u+u'x cos u=0</math> | ||
| + | :<math>\,u'x\cos u =-\sin u</math> | ||
| + | (itt megjegyzendő, hogy az u=kπ konstansok megoldások, azaz az eredetinek az y=kπx megoldásai) | ||
| + | :<math>\,\int-\frac{\cos u}{\sin u}\mathrm{d}u =\int\frac{\mathrm{d}x}{x}</math> | ||
| + | :<math>\,-\ln|\sin u| =\ln|x|+C</math> | ||
| + | :<math>\frac{1}{|\sin u|}=K_1|x|</math> | ||
| + | :<math>\,1=Kx\sin \frac{y}{x}</math> (K≠0) | ||
| + | |||
| + | ==Függvényegyütthatós elsőrendű lineáris d.e.== | ||
| + | :<math> | ||
| + | y'+\frac{2y}{x}=\sin(x^3+1)</math> | ||
| + | |||
| + | '''Mo.''' Homogén megoldása. y=0 konstans megoldás. | ||
| + | :<math>y'=-\frac{2y}{x}</math> | ||
| + | :<math>\frac{dy}{y}=-2\frac{dx}{x}</math> | ||
| + | :<math>\ln|y|=\ln|x|^{-2}+C</math> | ||
| + | Bolzano tétele miatt tetszőleges K valós számmal: | ||
| + | :<math>y=K\frac{1}{x^2}</math> | ||
| + | ami a homogén általános megoldása. | ||
| + | |||
| + | Inhomogén part. keresése | ||
| + | :<math>y(x)=K(x)\frac{1}{x^2}</math> | ||
| + | :<math> | ||
| + | K'(x)\frac{1}{x^2}+K(x)\frac{-2}{x^3}+K(x)\frac{2}{x^3}=\sin(x^3+1)</math> | ||
| + | :<math> | ||
| + | K'(x)=x^2\sin(x^3+1)</math> | ||
| + | :<math> | ||
| + | K'(x)=\frac{1}{3}3x^2\sin(x^3+1)</math> | ||
| + | :<math> | ||
| + | K(x)=-\frac{1}{3}\cos(x^3+1)</math> | ||
| + | :<math>y=K\frac{1}{x^2}-\frac{1}{3}\cos(x^3+1)\frac{1}{x^2}</math> | ||
| − | |||
| − | + | <center> | |
| + | {| class="wikitable" style="text-align:center" | ||
| + | |- bgcolor="#efefef" | ||
| + | |[[Matematika A3a 2008/2. gyakorlat |2. gyakorlat]] | ||
| + | |} | ||
| + | {| class="wikitable" style="text-align:center" | ||
| + | |- bgcolor="#efefef" | ||
| + | |[[Matematika A3a 2008/4. gyakorlat |4. gyakorlat]] | ||
| + | |} | ||
| + | </center> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Kategória:Matematika A3]] | [[Kategória:Matematika A3]] | ||
A lap jelenlegi, 2017. január 16., 19:20-kori változata
Tartalomjegyzék |
Integráló tényező
Általában egy P(x,y)dx+Q(x,y)dy=0 alakú differenciálegyenlet esetén nem teljesül a rot(P,Q)=0 feltétel. Esetenként azonban található olyan μ kétváltozós pozitív értékű függvény, amellyel:
már egzakt egyenlet. Vizsáljuk meg miből nyerhetjük az ilyen μ un. integráló szorzót! A rot(μP,μQ)=0 feltétel a következő:
Mivel
és ugyanígy
ezért
Ezt a parciális differenciálegyenletet kell megoldanunk ahhoz, hogy legyen integráló tényezőnk.
Speciális esetek
Megállapíthatjuk, hogy néha érdemes a μ-re felírt egyenletnek csak olyan megoldásait keresni, amelyek csak az egyik változótól függenek. Ez a következő esekben áll elő.
I. Keressük a megoldást a μ=μ(x) feltevéssel! Ekkor ln(μ)=ln(μ)(x) és ∂yln(μ)=0, azaz
és
csak x-től függ és innen az integráló szorzó:
Példa.
Az x>0, y tetszőleges kezdeti érték tarrtományban oldjuk meg az alábbi egyenletet!
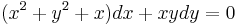 , (xyy' = − x2 − y2 − x)
, (xyy' = − x2 − y2 − x)
Mo. P = x2 + y2 + x, Q = xy, 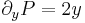 ,
, 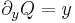 azaz nem egzakt, de
azaz nem egzakt, de
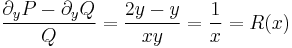 ,
, 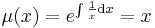
II. Keressük a megoldást a μ=μ(y) feltevéssel! Ekkor ln(μ)=ln(μ)(y) és ∂xln(μ)=0, azaz
és
csak y-től függ és innen az integráló szorzó:
Megj.: A gyakorlatban ilyenkor vesszük az
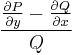 ill.
ill. 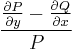
törteket és ellenőrizzük, hogy rendre csak x-től vagy csak y-tól függenek. Ha valamelyik, akkor azt a megoldást választjuk.
Példa.
Oldjuk meg az
egyenletet!
1. Mo. Nem egzakt:
Egzakttá tehető, ugyanis:
Emiatt
Megoldása:
2. Mo. Szeparábilis is.
III. Előfordulhat, hogy szeparábilis alakban kell keresnünk a parc. diff. egyenlet megoldását, azaz μ(x,y)=φ(x)ψ(y) alakban. Ekkor -- mint az könnyen ellenőrizhető -- az egyenlet
alakú és az integráló szorzó
Példa. Oldjuk meg az
egyenletet!
Mo. Átrendezve:
∂yP=3y2, ∂xQ=-y2, azaz
azaz célravezet, ha μ-t μ(x) alakban keressük. Ekkor
Ekkor az egyenlet:
egzakt, mert
Integrálássa:
azaz
Elméleti példák
1. Az y'=-P/Q homogén fokszámú egyenlet, melyben P és Q azonos fokszámú homogén függvények szintén egzakttá tehető az 1/(Px+Qy) szorzóval, ha ez nem az y'=-y/x egyenlet (ennek meg ismerjük a megoldását).
2. Keressünk integráló tényezőt az
közönséges elsőrendű inhomogén lineáris differenciálegyenlethez!
Világos, hogy nem egzakt, mert a
alakban a keresztben vett deriváltak: 0 és f(x).
Q=1 és P(x,y)=-g(x)+f(x)y ezért a μ-t adó parc.diff. egyenlet:
Elegendő egy partikuláris megoldást találni, amit egyszerűen megkapunk, ha csak az olyan μ-ket keressük, amik csak az x-től függenek, ekkor ugyanis pl. g(x) nem is lesz az egyenletben. Ilyet találunk, mert:
Ez egy szeparábilis, aminek a megoldása:
egy partikuláris megoldás:
ahol F'=f.
HF: Keressük meg ezzel az integáló szorzóval az általános megoldást!
Mo.
Már egzakt, hiszen
Ekkor
azaz
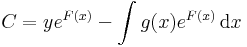
Gyakorlás
Oldja meg az alábbi egyenletet az a) y(π)=0 ill. b) y(2/π)=1 kezdeti feltétel mellett!
Mo. Legyen u = y / x, innen y' = u'x + u
(itt megjegyzendő, hogy az u=kπ konstansok megoldások, azaz az eredetinek az y=kπx megoldásai)
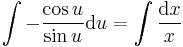
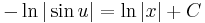
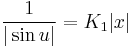
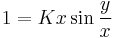 (K≠0)
(K≠0)
Függvényegyütthatós elsőrendű lineáris d.e.
Mo. Homogén megoldása. y=0 konstans megoldás.
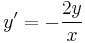
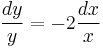
- ln | y | = ln | x | − 2 + C
Bolzano tétele miatt tetszőleges K valós számmal:
ami a homogén általános megoldása.
Inhomogén part. keresése
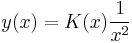
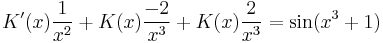
- K'(x) = x2sin(x3 + 1)
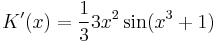
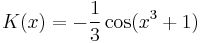
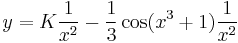
| 2. gyakorlat |
| 4. gyakorlat |
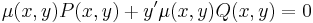
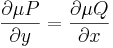
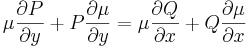
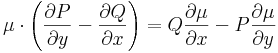
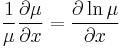
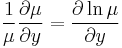
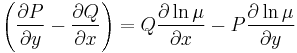
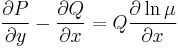
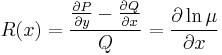
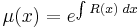
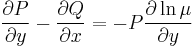
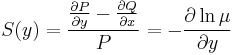
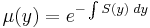
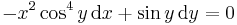
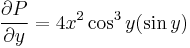
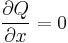
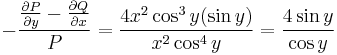
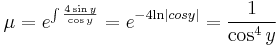
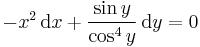
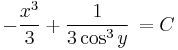
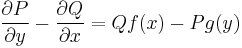
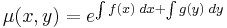
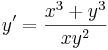
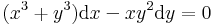
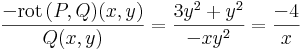
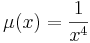
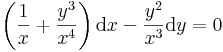
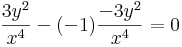
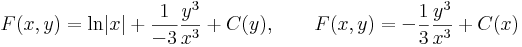
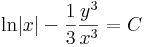
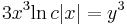
![x\sqrt[3]{3\,\mathrm{ln}\,c|x|}=y(x)\,](/upload/math/d/d/0/dd047c99fd5100a705896f6427be4de3.png)