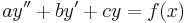Matematika A3a 2008/4. gyakorlat
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) (→Állandó együtthatós lineáris differenciálegyenlet) |
||
| 1. sor: | 1. sor: | ||
''<sub><[[Matematika A3a 2008]]</sub>'' | ''<sub><[[Matematika A3a 2008]]</sub>'' | ||
==Állandó együtthatós lineáris differenciálegyenlet== | ==Állandó együtthatós lineáris differenciálegyenlet== | ||
| + | |||
| + | Csak a másodrendű esetet tárgyaljuk: | ||
| + | :<math>ay''+by'+cy=f(x)\,</math> | ||
| + | ha ''a'', ''b'', ''c'' ∈ '''R'''. Ilyenkor a homogén egyenlet megoldását az ''a''λ<sup>2</sup>+''b''λ+''c''=0 karakterisztikus egyenlet megoldásából származó λ gyökökből száraztatjuk (bizonyítása a bizonyítások között). | ||
| + | |||
| + | :<math>y(x)=C_1e^{\lambda_1x}+C_2e^{\lambda_2x}</math>, ha <math>\lambda_1\ne\lambda_2\in\mathbf{R}\,</math> | ||
| + | :<math>y(x)=C_1e^{\lambda x}+C_2xe^{\lambda x}</math>, ha <math>\lambda_1=\lambda=\lambda\in\mathbf{R}\,</math> (gyök vagy belső rezonancia esete) | ||
| + | :<math>y(x)=C_1e^{\alpha x}\cos(\beta x)+C_2e^{\alpha x}\sin(\beta x)</math>, ha <math>\lambda_{1,2}=\alpha\pm\beta\in\mathbf{C}\,</math> | ||
| + | |||
| + | |||
| + | |||
<center> | <center> | ||
{| class="wikitable" style="text-align:center" | {| class="wikitable" style="text-align:center" | ||
| 11. sor: | 22. sor: | ||
|} | |} | ||
</center> | </center> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Kategória:Matematika A3]] | [[Kategória:Matematika A3]] | ||
A lap 2016. március 4., 22:48-kori változata
Állandó együtthatós lineáris differenciálegyenlet
Csak a másodrendű esetet tárgyaljuk:
ha a, b, c ∈ R. Ilyenkor a homogén egyenlet megoldását az aλ2+bλ+c=0 karakterisztikus egyenlet megoldásából származó λ gyökökből száraztatjuk (bizonyítása a bizonyítások között).
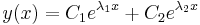, ha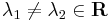 
- y(x) = C1eλx + C2xeλx, ha
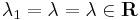(gyök vagy belső rezonancia esete)
- y(x) = C1eαxcos(βx) + C2eαxsin(βx), ha
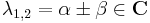
| 3. gyakorlat |
| 5. gyakorlat |
