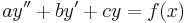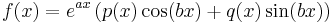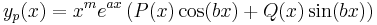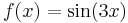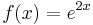Matematika A3a 2008/4. gyakorlat

A MathWikiből

(Változatok közti eltérés)

Ugrás: navigáció, keresés

A lap 2016. március 4., 23:10-kori változata

_{<Matematika A3a 2008}

Állandó együtthatós lineáris differenciálegyenlet

Csak a másodrendű esetet tárgyaljuk:

$ay''+by'+cy=f(x)\,$

ha a, b, c ∈ R.

Ilyenkor a homogén egyenlet megoldását az aλ²+bλ+c=0 karakterisztikus egyenlet megoldásából származó λ gyökökből száraztatjuk (bizonyítása a bizonyítások között).

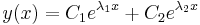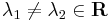
$y(x)=C_1e^{\lambda_1x}+C_2e^{\lambda_2x}$ , ha $\lambda_1\ne\lambda_2\in\mathbf{R}\,$

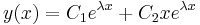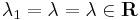$y(x)=C_1e^{\lambda x}+C_2xe^{\lambda x}\,$ , ha $\lambda_1=\lambda=\lambda\in\mathbf{R}\,$ (gyök vagy belső rezonancia esete)

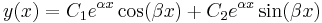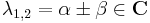
$y(x)=C_1e^{\alpha x}\cos(\beta x)+C_2e^{\alpha x}\sin(\beta x)\,$ , ha $\lambda_{1,2}=\alpha\pm\beta\in\mathbf{C}\,$

Az inhomogén egyenlet megoldását a következő alakban keressük. Ha az inhomogén tag az alábbi alakban írható

$f(x)=e^{ax}\left(p(x)\cos(bx)+q(x)\sin(bx)\right)$

ahol p(x) és q(x) polinomok és a a+ib ∈ C szám m szeres gyöke az aλ²+bλ+c karakterisztikus polinomnak, akkor az y_p(x) partikuláris megoldásra a feltevés:

$y_p(x)=x^me^{ax}\left(P(x)\cos(bx)+Q(x)\sin(bx)\right)$

ahol P(x) és Q(x) olyan polinomok, hogy deg P(x)=deg Q(x)= max{deg p(x), deg q(x)}.

Rezonanciák

1. $y''+9y=\sin(3x)\,$

Mo. $λ 2 + 9 = 0$ , azaz 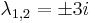$\lambda_{1,2}=\pm 3i\,$ . Innen

y H (x) = C 1 cos(3 x) + C 2 sin(3 x)

Mivel

$f(x)=\sin(3x)\,$

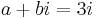ezért $a+bi=3i\,$ egyszeres megoldása a karakterisztikus egyenletnek, m=1 és az általános P(x), Q(x) polinomok konstansok: A,B, így az inhomogén egyenlet egy partikuláris megoldását az

y p (x) = A x cos(3 x) + B x sin(3 x)

alakban keresendő.

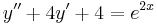
2. $y''+4y'+4=e^{2x}\,$

Mo. $λ 2 + 4λ + 4 = 0$ , azaz 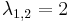$\lambda_{1,2}=2\,$ . Innen

y H (x) = C 1 e 2 x + C 2 e 2 x

Mivel

$f(x)=e^{2x}\,$

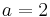ezért $a=2\,$ kétszeres megoldása a karakterisztikus egyenletnek, és ezért m=2 az általános P(x), Q(x) polinomok közül csak P(x) marad, mert b=0 lévén Q(x) kiesik, de P(x)=A állandó, így az inhomogén egyenlet egy partikuláris megoldását az

y p (x) = A x 2 e 2 x

alakban keresendő.

3. gyakorlat

5. gyakorlat

@@ 18. sor: / 18. sor: @@
 ahol P(x) és Q(x) olyan polinomok, hogy deg P(x)=deg Q(x)= max{deg p(x), deg q(x)}.
-===Példák===
+===Rezonanciák===
+'''1.''' <math>y''+9y=\sin(3x)\,</math>
+''Mo.'' <math>\lambda^2+9=0</math>, azaz <math>\lambda_{1,2}=\pm 3i\,</math>. Innen
+:<math>y_H(x)=C_1\cos(3x)+C_2\sin(3x)</math>
+Mivel
+:<math>f(x)=\sin(3x)\,</math>
+ezért <math>a+bi=3i\,</math> egyszeres megoldása a karakterisztikus egyenletnek, m=1 és az általános P(x), Q(x) polinomok konstansok: A,B, így az inhomogén egyenlet egy partikuláris megoldását az
+:<math>y_p(x)=Ax\cos(3x)+Bx\sin(3x)</math>
+alakban keresendő.
+'''2.''' <math>y''+4y'+4=e^{2x}\,</math>
+''Mo.'' <math>\lambda^2+4\lambda+4=0</math>, azaz <math>\lambda_{1,2}=2\,</math>. Innen
+:<math>y_H(x)=C_1e^{2x}+C_2e^{2x}</math>
+Mivel
+:<math>f(x)=e^{2x}\,</math>
+ezért <math>a=2\,</math> kétszeres megoldása a karakterisztikus egyenletnek, és ezért m=2 az általános P(x), Q(x) polinomok közül csak P(x) marad, mert b=0 lévén Q(x) kiesik, de P(x)=A állandó, így az inhomogén egyenlet egy partikuláris megoldását az
+:<math>y_p(x)=Ax^2e^{2x}</math>
+alakban keresendő.

Matematika A3a 2008/4. gyakorlat

A lap 2016. március 4., 23:10-kori változata

Állandó együtthatós lineáris differenciálegyenlet

Rezonanciák

Nézetek

Személyes eszközök

Navigáció

Keresés

Eszközök