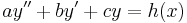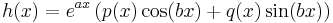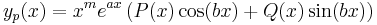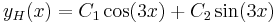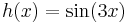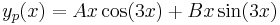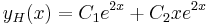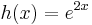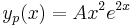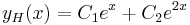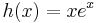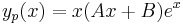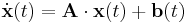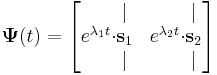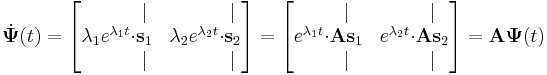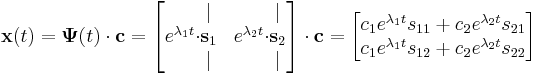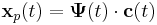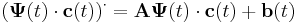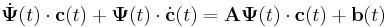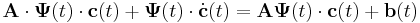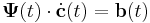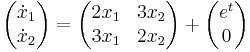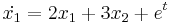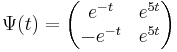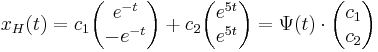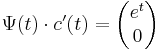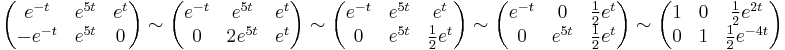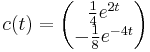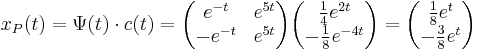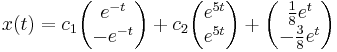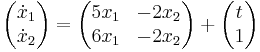Matematika A3a 2008/4. gyakorlat
Mozo (vitalap | szerkesztései) (→Rezonanciák) |
Mozo (vitalap | szerkesztései) (→Rezonanciák) |
||
| (egy szerkesztő 4 közbeeső változata nincs mutatva) | |||
| 3. sor: | 3. sor: | ||
Csak a másodrendű esetet tárgyaljuk: | Csak a másodrendű esetet tárgyaljuk: | ||
| − | :<math>ay''+by'+cy= | + | :<math>ay''+by'+cy=h(x)\,</math> |
ha ''a'', ''b'', ''c'' ∈ '''R'''. | ha ''a'', ''b'', ''c'' ∈ '''R'''. | ||
Ilyenkor a homogén egyenlet megoldását az ''a''λ<sup>2</sup>+''b''λ+''c''=0 karakterisztikus egyenlet megoldásából származó λ gyökökből száraztatjuk (bizonyítása a bizonyítások között). | Ilyenkor a homogén egyenlet megoldását az ''a''λ<sup>2</sup>+''b''λ+''c''=0 karakterisztikus egyenlet megoldásából származó λ gyökökből száraztatjuk (bizonyítása a bizonyítások között). | ||
| − | + | {| class="wikitable" | |
| − | + | |- | |
| − | + | | <math>\lambda_1\ne\lambda_2\in\mathbf{R}\,</math> | |
| + | | <math>y_H(x)=C_1e^{\lambda_1x}+C_2e^{\lambda_2x}</math> | ||
| + | |- | ||
| + | | <math>\lambda_1=\lambda_2=\lambda\in\mathbf{R}\,</math> | ||
| + | | <math>y_H(x)=C_1e^{\lambda x}+C_2xe^{\lambda x}\,</math> | ||
| + | |- | ||
| + | | <math>\lambda_{1,2}=\alpha\pm\beta i\in\mathbf{C}\,</math> | ||
| + | | <math>y_H(x)=C_1e^{\alpha x}\cos(\beta x)+C_2e^{\alpha x}\sin(\beta x)\,</math> | ||
| + | |} | ||
Az inhomogén egyenlet megoldását a következő alakban keressük. Ha az inhomogén tag az alábbi alakban írható | Az inhomogén egyenlet megoldását a következő alakban keressük. Ha az inhomogén tag az alábbi alakban írható | ||
| − | :<math> | + | :<math>h(x)=e^{ax}\left(p(x)\cos(bx)+q(x)\sin(bx)\right)</math> |
ahol p(x) és q(x) polinomok és a ''a''+i''b'' ∈ '''C''' szám ''m'' szeres gyöke az ''a''λ<sup>2</sup>+''b''λ+''c'' karakterisztikus polinomnak, akkor az y<sub>p</sub>(x) partikuláris megoldásra a feltevés: | ahol p(x) és q(x) polinomok és a ''a''+i''b'' ∈ '''C''' szám ''m'' szeres gyöke az ''a''λ<sup>2</sup>+''b''λ+''c'' karakterisztikus polinomnak, akkor az y<sub>p</sub>(x) partikuláris megoldásra a feltevés: | ||
:<math>y_p(x)=x^me^{ax}\left(P(x)\cos(bx)+Q(x)\sin(bx)\right)</math> | :<math>y_p(x)=x^me^{ax}\left(P(x)\cos(bx)+Q(x)\sin(bx)\right)</math> | ||
ahol P(x) és Q(x) olyan polinomok, hogy deg P(x)=deg Q(x)= max{deg p(x), deg q(x)}. | ahol P(x) és Q(x) olyan polinomok, hogy deg P(x)=deg Q(x)= max{deg p(x), deg q(x)}. | ||
| + | |||
| + | Ha '''nincs''' külső rezonancia, akkor az alábbi "szimbolikus" táblázat súg, hogy az inhomogén tag (gerjesztés) ismeretében milyen alakban keressük a partikuláris megoldást. (Ha van külső rezonancia, akkor annyiszor szorozzuk meg ''x''-szel ezt az értéket, hogy az már éppen lineárisan független legyen a homogén alapmegoldásoktól.) | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! <math>h(x)\,</math> | ||
| + | ! <math>y_P(x)\,</math> | ||
| + | |- | ||
| + | | <math>7x-8\,</math> | ||
| + | | <math>Ax+B\,</math> | ||
| + | |- | ||
| + | | <math>-x^2+\frac{1}{8}x-\sqrt{2}\,</math> | ||
| + | | <math>Ax^2+Bx+C\,</math> | ||
| + | |- | ||
| + | | <math>\frac{1}{7}e^{2x}\,</math> | ||
| + | | <math>Ae^{2x}\,</math> | ||
| + | |- | ||
| + | | <math>\sin(3x),\;\cos(3x)</math> | ||
| + | | <math>A\sin(3x)+B\cos(3x)\,</math> | ||
| + | |} | ||
===Rezonanciák=== | ===Rezonanciák=== | ||
| 22. sor: | 50. sor: | ||
''Mo.'' <math>\lambda^2+9=0\,</math>, azaz <math>\lambda_{1,2}=\pm 3i\,</math>. Innen | ''Mo.'' <math>\lambda^2+9=0\,</math>, azaz <math>\lambda_{1,2}=\pm 3i\,</math>. Innen | ||
| − | :<math>y_H(x)=C_1\cos(3x)+C_2\sin(3x)</math> | + | :<math>y_H(x)=C_1\cos(3x)+C_2\sin(3x)\,</math> |
Mivel | Mivel | ||
| − | :<math> | + | :<math>h(x)=\sin(3x)\,</math> |
ezért <math>a+bi=3i</math> egyszeres megoldása a karakterisztikus egyenletnek, m=1 és az általános P(x), Q(x) polinomok konstansok: A,B, így az inhomogén egyenlet egy partikuláris megoldását az | ezért <math>a+bi=3i</math> egyszeres megoldása a karakterisztikus egyenletnek, m=1 és az általános P(x), Q(x) polinomok konstansok: A,B, így az inhomogén egyenlet egy partikuláris megoldását az | ||
:<math>y_p(x)=Ax\cos(3x)+Bx\sin(3x)\,</math> | :<math>y_p(x)=Ax\cos(3x)+Bx\sin(3x)\,</math> | ||
| 32. sor: | 60. sor: | ||
''Mo.'' <math>\lambda^2-4\lambda+4=0\,</math>, azaz <math>\lambda_{1,2}=2\,</math>. Innen | ''Mo.'' <math>\lambda^2-4\lambda+4=0\,</math>, azaz <math>\lambda_{1,2}=2\,</math>. Innen | ||
| − | :<math>y_H(x)=C_1e^{2x}+ | + | :<math>y_H(x)=C_1e^{2x}+C_2xe^{2x}\,</math> |
Mivel | Mivel | ||
| − | :<math> | + | :<math>h(x)=e^{2x}\,</math> |
ezért <math>a=2</math> kétszeres megoldása a karakterisztikus egyenletnek, és ezért m=2 az általános P(x), Q(x) polinomok közül csak P(x) marad, mert b=0 lévén Q(x) kiesik, de P(x)=A állandó, így az inhomogén egyenlet egy partikuláris megoldását az | ezért <math>a=2</math> kétszeres megoldása a karakterisztikus egyenletnek, és ezért m=2 az általános P(x), Q(x) polinomok közül csak P(x) marad, mert b=0 lévén Q(x) kiesik, de P(x)=A állandó, így az inhomogén egyenlet egy partikuláris megoldását az | ||
:<math>y_p(x)=Ax^2e^{2x}\,</math> | :<math>y_p(x)=Ax^2e^{2x}\,</math> | ||
| 44. sor: | 72. sor: | ||
:<math>y_H(x)=C_1e^{x}+C_2e^{2x}\,</math> | :<math>y_H(x)=C_1e^{x}+C_2e^{2x}\,</math> | ||
Mivel | Mivel | ||
| − | :<math> | + | :<math>h(x)=xe^{x}\,</math> |
ezért <math>a=1</math> egyszeres megoldása a karakterisztikus egyenletnek, és ezért m=1 az általános P(x), Q(x) polinomok közül csak P(x) marad, mert b=0 lévén Q(x) kiesik (sin(0)=0), de P(x)=Ax+B elsőfokú, mert p(x)=x (hiszen cos(0)=1 és ez megmaradt), így az inhomogén egyenlet egy partikuláris megoldása az | ezért <math>a=1</math> egyszeres megoldása a karakterisztikus egyenletnek, és ezért m=1 az általános P(x), Q(x) polinomok közül csak P(x) marad, mert b=0 lévén Q(x) kiesik (sin(0)=0), de P(x)=Ax+B elsőfokú, mert p(x)=x (hiszen cos(0)=1 és ez megmaradt), így az inhomogén egyenlet egy partikuláris megoldása az | ||
:<math>y_p(x)=x(Ax+B)e^{x}\,</math> | :<math>y_p(x)=x(Ax+B)e^{x}\,</math> | ||
A lap jelenlegi, 2020. április 22., 14:46-kori változata
Tartalomjegyzék |
Állandó együtthatós lineáris differenciálegyenlet
Csak a másodrendű esetet tárgyaljuk:
ha a, b, c ∈ R.
Ilyenkor a homogén egyenlet megoldását az aλ2+bλ+c=0 karakterisztikus egyenlet megoldásából származó λ gyökökből száraztatjuk (bizonyítása a bizonyítások között).
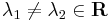
|
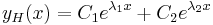
|
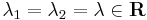
|
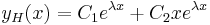
|
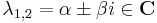
|
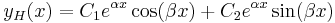
|
Az inhomogén egyenlet megoldását a következő alakban keressük. Ha az inhomogén tag az alábbi alakban írható
ahol p(x) és q(x) polinomok és a a+ib ∈ C szám m szeres gyöke az aλ2+bλ+c karakterisztikus polinomnak, akkor az yp(x) partikuláris megoldásra a feltevés:
ahol P(x) és Q(x) olyan polinomok, hogy deg P(x)=deg Q(x)= max{deg p(x), deg q(x)}.
Ha nincs külső rezonancia, akkor az alábbi "szimbolikus" táblázat súg, hogy az inhomogén tag (gerjesztés) ismeretében milyen alakban keressük a partikuláris megoldást. (Ha van külső rezonancia, akkor annyiszor szorozzuk meg x-szel ezt az értéket, hogy az már éppen lineárisan független legyen a homogén alapmegoldásoktól.)
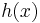
|
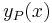
|
|---|---|
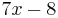
|
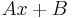
|
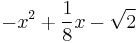
|
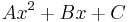
|
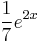
|
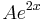
|
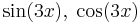
|
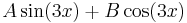
|
Rezonanciák
1. 
Mo. 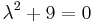 , azaz
, azaz 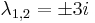 . Innen
. Innen
Mivel
ezért a + bi = 3i egyszeres megoldása a karakterisztikus egyenletnek, m=1 és az általános P(x), Q(x) polinomok konstansok: A,B, így az inhomogén egyenlet egy partikuláris megoldását az
alakban keresendő.
2. 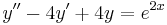
Mo.  , azaz
, azaz 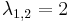 . Innen
. Innen
Mivel
ezért a = 2 kétszeres megoldása a karakterisztikus egyenletnek, és ezért m=2 az általános P(x), Q(x) polinomok közül csak P(x) marad, mert b=0 lévén Q(x) kiesik, de P(x)=A állandó, így az inhomogén egyenlet egy partikuláris megoldását az
alakban keresendő.
3. 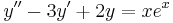
Mo. 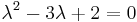 , azaz
, azaz 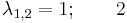 . Innen
. Innen
Mivel
ezért a = 1 egyszeres megoldása a karakterisztikus egyenletnek, és ezért m=1 az általános P(x), Q(x) polinomok közül csak P(x) marad, mert b=0 lévén Q(x) kiesik (sin(0)=0), de P(x)=Ax+B elsőfokú, mert p(x)=x (hiszen cos(0)=1 és ez megmaradt), így az inhomogén egyenlet egy partikuláris megoldása az
alakban keresendő.
Állandó együtthatós elsőrendű inhomogén lineáris differenciálegyenletrendszer
Az
egyenletrendszerben A konstans valós mátrix, b(t) vektorfüggvény. Csak azt az esetet vizsgáljuk, amikor A-nak vannak független sajátvektorai.
A homogén egyenlet megoldását az úgy nevezett mátrix alapmegoldásból állítjuk elő. Keresünk tehát olyan 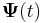 mátrixfüggvényt, melyre:
mátrixfüggvényt, melyre:
Belátjuk, hogy erre az A mátrix 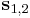 sajátvektoraiból összerakott
sajátvektoraiból összerakott
mátrixfüggvény, alkalmas, ahol persze 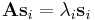 (i=1;2). Ugyanis
(i=1;2). Ugyanis
Ilyenkor pedig a megoldás tetszőleges 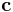 konstans általános vektorral:
konstans általános vektorral:
Az inhomohén egy partikuláris megoldását a következőképpen keressük meg. Feltesszük az állandó variálása módszerével, hogy
Ezt behelyettesítve az inhomogén egyenletbe kapjuk, hogy
De mivel tudjuk, hogy 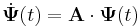 , ezért
, ezért
Ezért kiejtve, amit ki lehet, csak az
paraméteres egyenletrendszert kell megoldani 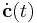 -re.
-re.
Példák
4.
Mo.
Homogén:
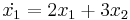
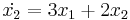
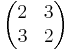 karakterisztikus polinomjának megoldásai: λ = − 1;5
karakterisztikus polinomjának megoldásai: λ = − 1;5
Sajátvektorai rendre: (1,-1), (1,1) ezekből a megoldás. Innen
és
Inhomogén:
Gauss--Jordan-nal:
5.
| 3. gyakorlat |
| 5. gyakorlat |