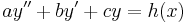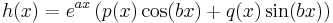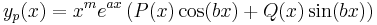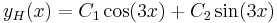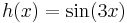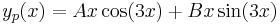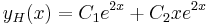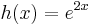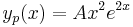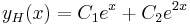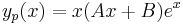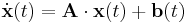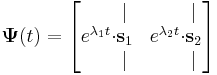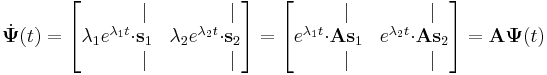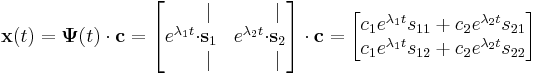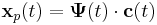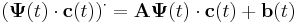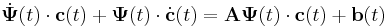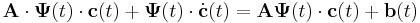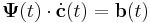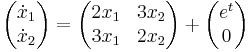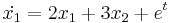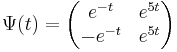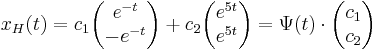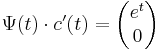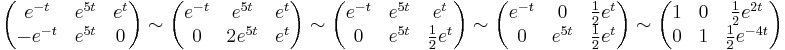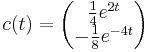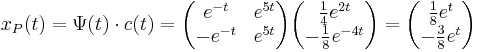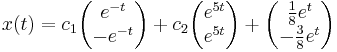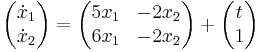Matematika A3a 2008/4. gyakorlat
Mozo (vitalap | szerkesztései) (→Homogén fokszámú egyenletek) |
Mozo (vitalap | szerkesztései) (→Rezonanciák) |
||
| (egy szerkesztő 44 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
''<sub><[[Matematika A3a 2008]]</sub>'' | ''<sub><[[Matematika A3a 2008]]</sub>'' | ||
| + | ==Állandó együtthatós lineáris differenciálegyenlet== | ||
| − | = | + | Csak a másodrendű esetet tárgyaljuk: |
| + | :<math>ay''+by'+cy=h(x)\,</math> | ||
| + | ha ''a'', ''b'', ''c'' ∈ '''R'''. | ||
| − | ''' | + | Ilyenkor a homogén egyenlet megoldását az ''a''λ<sup>2</sup>+''b''λ+''c''=0 karakterisztikus egyenlet megoldásából származó λ gyökökből száraztatjuk (bizonyítása a bizonyítások között). |
| − | + | ||
| − | '' | + | |
| − | + | ||
| − | + | ||
| − | + | {| class="wikitable" | |
| − | + | |- | |
| − | + | | <math>\lambda_1\ne\lambda_2\in\mathbf{R}\,</math> | |
| − | + | | <math>y_H(x)=C_1e^{\lambda_1x}+C_2e^{\lambda_2x}</math> | |
| − | + | |- | |
| − | + | | <math>\lambda_1=\lambda_2=\lambda\in\mathbf{R}\,</math> | |
| − | + | | <math>y_H(x)=C_1e^{\lambda x}+C_2xe^{\lambda x}\,</math> | |
| − | + | |- | |
| + | | <math>\lambda_{1,2}=\alpha\pm\beta i\in\mathbf{C}\,</math> | ||
| + | | <math>y_H(x)=C_1e^{\alpha x}\cos(\beta x)+C_2e^{\alpha x}\sin(\beta x)\,</math> | ||
| + | |} | ||
| − | + | Az inhomogén egyenlet megoldását a következő alakban keressük. Ha az inhomogén tag az alábbi alakban írható | |
| + | :<math>h(x)=e^{ax}\left(p(x)\cos(bx)+q(x)\sin(bx)\right)</math> | ||
| + | ahol p(x) és q(x) polinomok és a ''a''+i''b'' ∈ '''C''' szám ''m'' szeres gyöke az ''a''λ<sup>2</sup>+''b''λ+''c'' karakterisztikus polinomnak, akkor az y<sub>p</sub>(x) partikuláris megoldásra a feltevés: | ||
| + | :<math>y_p(x)=x^me^{ax}\left(P(x)\cos(bx)+Q(x)\sin(bx)\right)</math> | ||
| + | ahol P(x) és Q(x) olyan polinomok, hogy deg P(x)=deg Q(x)= max{deg p(x), deg q(x)}. | ||
| − | + | Ha '''nincs''' külső rezonancia, akkor az alábbi "szimbolikus" táblázat súg, hogy az inhomogén tag (gerjesztés) ismeretében milyen alakban keressük a partikuláris megoldást. (Ha van külső rezonancia, akkor annyiszor szorozzuk meg ''x''-szel ezt az értéket, hogy az már éppen lineárisan független legyen a homogén alapmegoldásoktól.) | |
| − | = | + | {| class="wikitable" |
| + | |- | ||
| + | ! <math>h(x)\,</math> | ||
| + | ! <math>y_P(x)\,</math> | ||
| + | |- | ||
| + | | <math>7x-8\,</math> | ||
| + | | <math>Ax+B\,</math> | ||
| + | |- | ||
| + | | <math>-x^2+\frac{1}{8}x-\sqrt{2}\,</math> | ||
| + | | <math>Ax^2+Bx+C\,</math> | ||
| + | |- | ||
| + | | <math>\frac{1}{7}e^{2x}\,</math> | ||
| + | | <math>Ae^{2x}\,</math> | ||
| + | |- | ||
| + | | <math>\sin(3x),\;\cos(3x)</math> | ||
| + | | <math>A\sin(3x)+B\cos(3x)\,</math> | ||
| + | |} | ||
| − | + | ===Rezonanciák=== | |
| − | + | '''1.''' <math>y''+9y=\sin(3x)\,</math> | |
| − | + | ||
| − | + | ||
| − | + | ''Mo.'' <math>\lambda^2+9=0\,</math>, azaz <math>\lambda_{1,2}=\pm 3i\,</math>. Innen | |
| − | + | :<math>y_H(x)=C_1\cos(3x)+C_2\sin(3x)\,</math> | |
| − | + | Mivel | |
| − | :<math> | + | :<math>h(x)=\sin(3x)\,</math> |
| − | + | ezért <math>a+bi=3i</math> egyszeres megoldása a karakterisztikus egyenletnek, m=1 és az általános P(x), Q(x) polinomok konstansok: A,B, így az inhomogén egyenlet egy partikuláris megoldását az | |
| + | :<math>y_p(x)=Ax\cos(3x)+Bx\sin(3x)\,</math> | ||
| + | alakban keresendő. | ||
| − | + | '''2.''' <math>y''-4y'+4y=e^{2x}\,</math> | |
| − | + | ''Mo.'' <math>\lambda^2-4\lambda+4=0\,</math>, azaz <math>\lambda_{1,2}=2\,</math>. Innen | |
| − | :<math> | + | :<math>y_H(x)=C_1e^{2x}+C_2xe^{2x}\,</math> |
| + | Mivel | ||
| + | :<math>h(x)=e^{2x}\,</math> | ||
| + | ezért <math>a=2</math> kétszeres megoldása a karakterisztikus egyenletnek, és ezért m=2 az általános P(x), Q(x) polinomok közül csak P(x) marad, mert b=0 lévén Q(x) kiesik, de P(x)=A állandó, így az inhomogén egyenlet egy partikuláris megoldását az | ||
| + | :<math>y_p(x)=Ax^2e^{2x}\,</math> | ||
| + | alakban keresendő. | ||
| − | + | '''3.''' <math>y''-3y'+2y=xe^{x}\,</math> | |
| − | + | ''Mo.'' <math>\lambda^2-3\lambda+2=0\,</math>, azaz <math>\lambda_{1,2}=1;\qquad 2\,</math>. Innen | |
| + | :<math>y_H(x)=C_1e^{x}+C_2e^{2x}\,</math> | ||
| + | Mivel | ||
| + | :<math>h(x)=xe^{x}\,</math> | ||
| + | ezért <math>a=1</math> egyszeres megoldása a karakterisztikus egyenletnek, és ezért m=1 az általános P(x), Q(x) polinomok közül csak P(x) marad, mert b=0 lévén Q(x) kiesik (sin(0)=0), de P(x)=Ax+B elsőfokú, mert p(x)=x (hiszen cos(0)=1 és ez megmaradt), így az inhomogén egyenlet egy partikuláris megoldása az | ||
| + | :<math>y_p(x)=x(Ax+B)e^{x}\,</math> | ||
| + | alakban keresendő. | ||
| − | + | ==Állandó együtthatós elsőrendű inhomogén lineáris differenciálegyenletrendszer== | |
| + | Az | ||
| + | :<math>\dot{\mathbf{x}}(t)=\mathbf{A}\cdot\mathbf{x}(t)+\mathbf{b}(t)</math> | ||
| + | egyenletrendszerben '''A''' konstans valós mátrix, '''b'''(t) vektorfüggvény. Csak azt az esetet vizsgáljuk, amikor '''A'''-nak vannak független sajátvektorai. | ||
| − | ''' | + | A homogén egyenlet megoldását az úgy nevezett mátrix alapmegoldásból állítjuk elő. Keresünk tehát olyan <math>\mathbf{\Psi}(t)</math> mátrixfüggvényt, melyre: |
| − | === | + | :<math>\dot{\mathbf{\Psi}}(t)=\mathbf{A}\cdot\mathbf{\Psi}(t)</math> |
| + | Belátjuk, hogy erre az '''A''' mátrix <math>\mathbf{s}_{1,2}</math> sajátvektoraiból összerakott | ||
| + | :<math>\mathbf{\Psi}(t)= | ||
| + | \begin{bmatrix} | ||
| + | & | & & |\\ | ||
| + | e^{\lambda_1 t}\cdot\!\!\!\!\! & \mathbf{s}_1 & e^{\lambda_2 t}\cdot\!\!\!\!\! & \mathbf{s}_2\\ | ||
| + | & | & & | | ||
| + | \end{bmatrix}</math> | ||
| + | mátrixfüggvény, alkalmas, ahol persze <math>\mathbf{As}_i=\lambda_i\mathbf{s}_i</math> (i=1;2). Ugyanis | ||
| + | :<math>\dot{\mathbf{\Psi}}(t)= | ||
| + | \begin{bmatrix} | ||
| + | & | & & |\\ | ||
| + | \lambda_1e^{\lambda_1 t}\cdot\!\!\!\!\! & \mathbf{s}_1 & \lambda_2e^{\lambda_2 t}\cdot\!\!\!\!\! & \mathbf{s}_2\\ | ||
| + | & | & & | | ||
| + | \end{bmatrix}=\begin{bmatrix} | ||
| + | & | & & |\\ | ||
| + | e^{\lambda_1 t}\cdot\!\!\!\!\! & \mathbf{As}_1 & e^{\lambda_2 t}\cdot\!\!\!\!\! & \mathbf{As}_2\\ | ||
| + | & | & & | | ||
| + | \end{bmatrix}=\mathbf{A\Psi}(t)</math> | ||
| + | Ilyenkor pedig a megoldás tetszőleges <math>\mathbf{c}</math> konstans általános vektorral: | ||
| + | :<math>\mathbf{x}(t)=\mathbf{\Psi}(t)\cdot \mathbf{c}=\begin{bmatrix} | ||
| + | & | & & |\\ | ||
| + | e^{\lambda_1 t}\cdot\!\!\!\!\! & \mathbf{s}_1 & e^{\lambda_2 t}\cdot\!\!\!\!\! & \mathbf{s}_2\\ | ||
| + | & | & & | | ||
| + | \end{bmatrix}\cdot \mathbf{c}=\begin{bmatrix}c_1e^{\lambda_1 t}s_{11}+c_2e^{\lambda_2 t}s_{21}\\c_1e^{\lambda_1 t}s_{12}+c_2e^{\lambda_2 t}s_{22}\end{bmatrix}</math> | ||
| + | Az inhomohén egy partikuláris megoldását a következőképpen keressük meg. Feltesszük az állandó variálása módszerével, hogy | ||
| + | :<math>\mathbf{x}_p(t)=\mathbf{\Psi}(t)\cdot \mathbf{c}(t)</math> | ||
| + | Ezt behelyettesítve az inhomogén egyenletbe kapjuk, hogy | ||
| + | :<math>(\mathbf{\Psi}(t)\cdot \mathbf{c}(t))^\cdot=\mathbf{A\Psi}(t)\cdot \mathbf{c}(t)+\mathbf{b}(t)</math> | ||
| + | :<math>\dot{\mathbf{\Psi}}(t)\cdot \mathbf{c}(t)+\mathbf{\Psi}(t)\cdot \dot{\mathbf{c}}(t)=\mathbf{A\Psi}(t)\cdot \mathbf{c}(t)+\mathbf{b}(t)</math> | ||
| + | De mivel tudjuk, hogy <math>\dot{\mathbf{\Psi}}(t)=\mathbf{A}\cdot\mathbf{\Psi}(t)</math>, ezért | ||
| + | :<math>\mathbf{A}\cdot\mathbf{\Psi}(t)\cdot \mathbf{c}(t)+\mathbf{\Psi}(t)\cdot \dot{\mathbf{c}}(t)=\mathbf{A\Psi}(t)\cdot \mathbf{c}(t)+\mathbf{b}(t)</math> | ||
| + | Ezért kiejtve, amit ki lehet, csak az | ||
| + | :<math>\mathbf{\Psi}(t)\cdot \dot{\mathbf{c}}(t)=\mathbf{b}(t)</math> | ||
| + | paraméteres egyenletrendszert kell megoldani <math>\dot{\mathbf{c}}(t)</math>-re. | ||
| − | + | ===Példák=== | |
| − | ''' | + | '''4.''' |
| + | :<math>\begin{pmatrix}\dot{x}_1\\\dot{x}_2\end{pmatrix}=\begin{pmatrix}2x_1 & 3x_2\\ 3x_1 & 2x_2\end{pmatrix}+\begin{pmatrix}e^t\\0\end{pmatrix}</math> | ||
| + | '''Mo.''' | ||
| + | :<math>\dot{x_1}=2x_1+3x_2+e^t</math> | ||
| + | :<math>\dot{x_2}=3x_1+2x_2</math> | ||
| + | Homogén: | ||
| + | :<math>\dot{x_1}=2x_1+3x_2</math> | ||
| + | :<math>\dot{x_2}=3x_1+2x_2</math> | ||
| + | :<math>\begin{pmatrix}2 & 3\\3 & 2\end{pmatrix}</math> karakterisztikus polinomjának megoldásai: <math>\lambda=-1; 5 | ||
| + | </math> | ||
| + | Sajátvektorai rendre: (1,-1), (1,1) ezekből a megoldás. Innen | ||
| + | :<math>\Psi(t)=\begin{pmatrix}e^{-t} & e^{5t}\\-e^{-t} & e^{5t}\end{pmatrix}</math> | ||
| + | és | ||
| + | :<math>x_H(t)=c_1\begin{pmatrix}e^{-t}\\-e^{-t}\end{pmatrix}+c_2\begin{pmatrix}e^{5t}\\e^{5t}\end{pmatrix}=\Psi(t)\cdot\begin{pmatrix}c_1\\c_2\end{pmatrix}</math> | ||
| + | Inhomogén: | ||
| + | :<math>\Psi(t)\cdot c'(t)=\begin{pmatrix}e^{t}\\0\end{pmatrix}</math> | ||
| + | Gauss--Jordan-nal: | ||
| + | :<math>\begin{pmatrix}e^{-t} & e^{5t}& e^{t}\\-e^{-t} & e^{5t}& 0\end{pmatrix}\sim\begin{pmatrix}e^{-t} & e^{5t}& e^{t}\\0 & 2e^{5t}& e^{t}\end{pmatrix}\sim\begin{pmatrix}e^{-t} & e^{5t}& e^{t}\\0 & e^{5t}& \frac{1}{2}e^{t}\end{pmatrix}\sim \begin{pmatrix}e^{-t} & 0 & \frac{1}{2}e^{t}\\0 & e^{5t}& \frac{1}{2}e^{t}\end{pmatrix}\sim\begin{pmatrix}1 & 0 & \frac{1}{2}e^{2t}\\0 & 1& \frac{1}{2}e^{-4t}\end{pmatrix}</math> | ||
| + | :<math> c(t)=\begin{pmatrix}\frac{1}{4}e^{2t}\\ -\frac{1}{8}e^{-4t}\end{pmatrix}</math> | ||
| + | :<math> x_P(t)=\Psi(t)\cdot c(t)=\begin{pmatrix}e^{-t} & e^{5t}\\-e^{-t} & e^{5t}\end{pmatrix}\begin{pmatrix}\frac{1}{4}e^{2t}\\ -\frac{1}{8}e^{-4t}\end{pmatrix}=\begin{pmatrix}\frac{1}{8}e^{t}\\ -\frac{3}{8}e^{t}\end{pmatrix}</math> | ||
| + | :<math>x(t)=c_1\begin{pmatrix}e^{-t}\\-e^{-t}\end{pmatrix}+c_2\begin{pmatrix}e^{5t}\\e^{5t}\end{pmatrix}+\begin{pmatrix}\frac{1}{8}e^{t}\\ -\frac{3}{8}e^{t}\end{pmatrix}</math> | ||
| − | = | + | '''5.''' |
| + | :<math>\begin{pmatrix}\dot{x}_1\\\dot{x}_2\end{pmatrix}=\begin{pmatrix}5x_1 & -2x_2\\ 6x_1 & -2x_2\end{pmatrix}+\begin{pmatrix}t\\1\end{pmatrix}</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <center> | ||
| + | {| class="wikitable" style="text-align:center" | ||
| + | |- bgcolor="#efefef" | ||
| + | |[[Matematika A3a 2008/3. gyakorlat |3. gyakorlat]] | ||
| + | |} | ||
| + | {| class="wikitable" style="text-align:center" | ||
| + | |- bgcolor="#efefef" | ||
| + | |[[Matematika A3a 2008/5. gyakorlat |5. gyakorlat]] | ||
| + | |} | ||
| + | </center> | ||
[[Kategória:Matematika A3]] | [[Kategória:Matematika A3]] | ||
A lap jelenlegi, 2020. április 22., 14:46-kori változata
Tartalomjegyzék |
Állandó együtthatós lineáris differenciálegyenlet
Csak a másodrendű esetet tárgyaljuk:
ha a, b, c ∈ R.
Ilyenkor a homogén egyenlet megoldását az aλ2+bλ+c=0 karakterisztikus egyenlet megoldásából származó λ gyökökből száraztatjuk (bizonyítása a bizonyítások között).
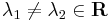
|
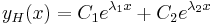
|
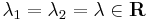
|
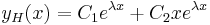
|
|
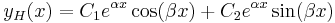
|
Az inhomogén egyenlet megoldását a következő alakban keressük. Ha az inhomogén tag az alábbi alakban írható
ahol p(x) és q(x) polinomok és a a+ib ∈ C szám m szeres gyöke az aλ2+bλ+c karakterisztikus polinomnak, akkor az yp(x) partikuláris megoldásra a feltevés:
ahol P(x) és Q(x) olyan polinomok, hogy deg P(x)=deg Q(x)= max{deg p(x), deg q(x)}.
Ha nincs külső rezonancia, akkor az alábbi "szimbolikus" táblázat súg, hogy az inhomogén tag (gerjesztés) ismeretében milyen alakban keressük a partikuláris megoldást. (Ha van külső rezonancia, akkor annyiszor szorozzuk meg x-szel ezt az értéket, hogy az már éppen lineárisan független legyen a homogén alapmegoldásoktól.)
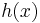
|
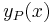
|
|---|---|
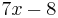
|
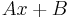
|
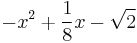
|
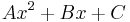
|
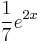
|
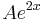
|
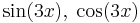
|
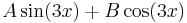
|
Rezonanciák
1. 
Mo. 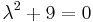 , azaz
, azaz 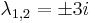 . Innen
. Innen
Mivel
ezért a + bi = 3i egyszeres megoldása a karakterisztikus egyenletnek, m=1 és az általános P(x), Q(x) polinomok konstansok: A,B, így az inhomogén egyenlet egy partikuláris megoldását az
alakban keresendő.
2. 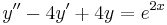
Mo. 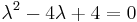 , azaz
, azaz 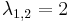 . Innen
. Innen
Mivel
ezért a = 2 kétszeres megoldása a karakterisztikus egyenletnek, és ezért m=2 az általános P(x), Q(x) polinomok közül csak P(x) marad, mert b=0 lévén Q(x) kiesik, de P(x)=A állandó, így az inhomogén egyenlet egy partikuláris megoldását az
alakban keresendő.
3. 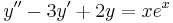
Mo. 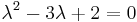 , azaz
, azaz 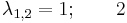 . Innen
. Innen
Mivel
ezért a = 1 egyszeres megoldása a karakterisztikus egyenletnek, és ezért m=1 az általános P(x), Q(x) polinomok közül csak P(x) marad, mert b=0 lévén Q(x) kiesik (sin(0)=0), de P(x)=Ax+B elsőfokú, mert p(x)=x (hiszen cos(0)=1 és ez megmaradt), így az inhomogén egyenlet egy partikuláris megoldása az
alakban keresendő.
Állandó együtthatós elsőrendű inhomogén lineáris differenciálegyenletrendszer
Az
egyenletrendszerben A konstans valós mátrix, b(t) vektorfüggvény. Csak azt az esetet vizsgáljuk, amikor A-nak vannak független sajátvektorai.
A homogén egyenlet megoldását az úgy nevezett mátrix alapmegoldásból állítjuk elő. Keresünk tehát olyan 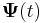 mátrixfüggvényt, melyre:
mátrixfüggvényt, melyre:
Belátjuk, hogy erre az A mátrix 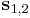 sajátvektoraiból összerakott
sajátvektoraiból összerakott
mátrixfüggvény, alkalmas, ahol persze 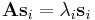 (i=1;2). Ugyanis
(i=1;2). Ugyanis
Ilyenkor pedig a megoldás tetszőleges 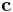 konstans általános vektorral:
konstans általános vektorral:
Az inhomohén egy partikuláris megoldását a következőképpen keressük meg. Feltesszük az állandó variálása módszerével, hogy
Ezt behelyettesítve az inhomogén egyenletbe kapjuk, hogy
De mivel tudjuk, hogy 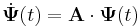 , ezért
, ezért
Ezért kiejtve, amit ki lehet, csak az
paraméteres egyenletrendszert kell megoldani 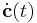 -re.
-re.
Példák
4.
Mo.
Homogén:
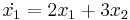
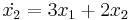
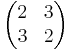 karakterisztikus polinomjának megoldásai: λ = − 1;5
karakterisztikus polinomjának megoldásai: λ = − 1;5
Sajátvektorai rendre: (1,-1), (1,1) ezekből a megoldás. Innen
és
Inhomogén:
Gauss--Jordan-nal:
5.
| 3. gyakorlat |
| 5. gyakorlat |