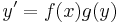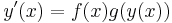Matematika A3a 2008/4. gyakorlat
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) (→Szeparábilis differenciálegyenlet) |
||
| 22. sor: | 22. sor: | ||
(0,1)-en áthaladó megoldás a C = 8/7-es görbe. | (0,1)-en áthaladó megoldás a C = 8/7-es görbe. | ||
| + | ===Általános módszer=== | ||
| + | |||
| + | Legyen ''f'' : ''I'' <math>\to</math> '''R''', ''g'': ''J'' <math>\to</math> '''R''' intervallumon értelmezett folytonos függvények, ahol ''g'' sehol sem nulla. Ekkor az y: ''K'' <math>\to</math> '''J''' differenciálható függvény, ahol ''K'' ⊆ ''I'' megoldása az | ||
| + | :<math>y'=f(x)g(y)\,</math> | ||
| + | un. szeparábilis diffegyenletnek, ha minden ''x'' ∈ ''K''-ra: | ||
| + | :<math>y'(x)=f(x)g(y(x))\,</math> | ||
[[Kategória:Matematika A3]] | [[Kategória:Matematika A3]] | ||
A lap 2008. október 9., 12:05-kori változata
Szeparábilis differenciálegyenlet
1. Feladat. Milyen függvények elégítik ki az alábbi differenciálegynletet. Van-e olyan, mely a 0-ban 0-t vesz föl, illetve a 0-ban 1-et?
Megoldás. Nyilván a megoldás sehol sem vehet föl nulla értéket, mert akkor
ott nem lenne értelmezve.
A mechanikus megoldási eljárás a következő:
ez az implicit általános megoldás és
az explicit általános megoldás.
A megoldás mechanikus megkeresése után meg kell jegyeznünk, hogy csak olyan intervallumokra kell szorítkoznunk, ahol az y nem ad nullát. Ezeken belül vannak olyan esetek, melyek nem is differenciálhatók a 7. gyök miatt.
(0,1)-en áthaladó megoldás a C = 8/7-es görbe.
Általános módszer
Legyen f : I  R, g: J
R, g: J  R intervallumon értelmezett folytonos függvények, ahol g sehol sem nulla. Ekkor az y: K
R intervallumon értelmezett folytonos függvények, ahol g sehol sem nulla. Ekkor az y: K  J differenciálható függvény, ahol K ⊆ I megoldása az
J differenciálható függvény, ahol K ⊆ I megoldása az
un. szeparábilis diffegyenletnek, ha minden x ∈ K-ra:
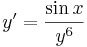
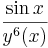
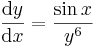
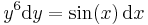
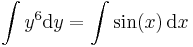
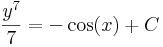
![y(x)=\sqrt[7]{-7\cos(x)+C}\,](/upload/math/e/2/d/e2d7f66e9664a8ea1ef763c670f9b58c.png)