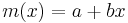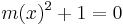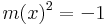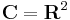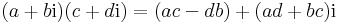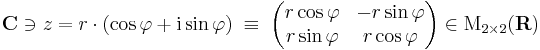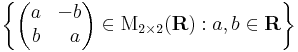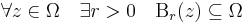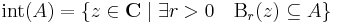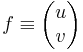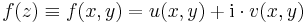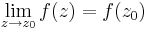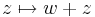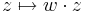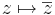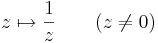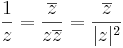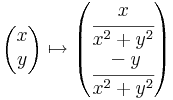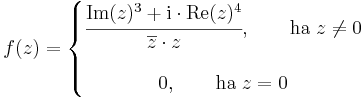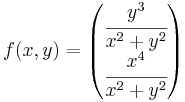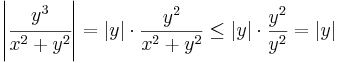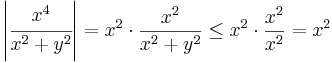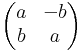Matematika A3a 2008/4. gyakorlat
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) (→Szeparábilis differenciálegyenlet) |
||
| 179. sor: | 179. sor: | ||
[[Kategória:Matematika A3]] | [[Kategória:Matematika A3]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Kategória:Matematika A3]] | [[Kategória:Matematika A3]] | ||
A lap 2013. szeptember 8., 08:49-kori változata
Tartalomjegyzék |
Komplex számkör és reprezentációi
A komplex számok C halmazát és műveleteit legalább három, lényegesen más szemszögből lehet láttatni. A meghatározottság kedvéért összefoglaljuk a komplex számok legfontosabb algebrai tulajdonságait. Nem térünk ki minden egyes műveleti tulajdonságra, ezek megtalálhatók a komplex számok algebráját leíró tankönyvekben.
Algebrai modell
A komplex számok olyan
alakú formális kifejezések, ahol a és b valós számok, i pedig azzal a speciális tulajdonsággal rendelkezik, hogy
A komplex számok halmazát a C szimbólummal jelöljük, tehát
itt a-t a z valós részének nevezzük és Re(z)-vel jelöljük, b-t a z képzetes részének nevezzük és Im(z)-vel jelöljük. Világos, hogy Im(z) ∈ R, azaz "tiszta" valós.
Megjegyzés. A kevéssé informatív "formális kifejezés" helyett bevezethetjük a komplex számokat valódi algebrai objektumokként. A komplex számok halmazát egy a maradékos osztással rendelkező halmazból konstrulájuk: a valós együtthatós polinomok R[X] halmazából. Közismert, hogy a valósegyütthatós, egyhatározatlanú polinomokal, azaz a
alakú kifejezésekkel, ahol az ai-k valós számok, n pedig nemnegatív egész, lehet maradékosan osztani (polinomosztás). Ekkor
azaz a komplex számok halmaza a valósegyütthatós polinomok x2+1 polinommal történő osztási maradékai. Világos, hogy minden ilyen maradék előáll
alakban, azaz legfeljebb elsőfokú polinom alakjában. Ebben a számkörben az összeadás a polinomösszeadás, a szorzás a polinomok szorzása (illetve ezen eredményének x2+1-vel történő osztási maradéka). Amikor két elsőfokú polinom szorzata másodfokú, akkor sem lépünk ki a számkörből, hisz a
polinomegyenlet megoldható, éspedig az m(x)=x polinom (az identitás) megoldás. Ekkor
azaz ebben a számkörben létezik a -1-nek négyzetgyöke. Az m(x)=x polinom az, mely az i egység szerepét játssza és így is jelöljük ezt ezentúl.
Akárcsak a legfeljebb elsőfokú a + bx alakú polinomok esetén, a C-t alkotó formális kifejezések között is értelmezhetjük az összeadást és a szorzást. Ezeket pontosan úgy definiáljuk, mint az a + bx alakú polinomok összegét és szorzatát, azzal a specialitással, hogy ahol a polinomok a szorzást követően másodfokúvá válnak, ott a komplex számok az i2=-1 egyenlőség miatt visszaérkeznek az a + bi alakú kifejezések körébe. Ezért lesz C zárt arra a szorzásra, amit a polinomok mintájára definiálunk.
Már innen is látszik, hogy a komplex számok halmaza kétdimenziós valós test feletti vektortér. Kimondhatjuk tehát:
Állítás. A C számkör a komplex számok
- (a+bi) + (c+di) = (a+c) + (b+d)i összeadásával és a
- λ(a+bi) = λa + λbi, a λ valós számmal való szorzással
kétdimenziós valós vektorteret alkotnak és így lineárisan izomorfak a valós számpárok R2 vektorterével.
Halmazelméleti modell
Az algebrai modellben nem teljesen világos, hogy mi is az i elem. Az előző állítás azonban lehetőséget biztosít arra, hogy konkrétan megadjuk a komplex számok halmazát mindenféle olyan kifejezés használata nélkül, mint "formális kifejezés" stb. (Valójában persze az algebrai modell is jól értelmezett módon adja meg a komplex számok halmazát, ha az a + bi alakú formális kifejezéseken az R[X] polinomgyűrűnek az (1+X2) polinommal történő maradékos osztásának maradékait értjük).
A számpár reprezentációban:
az összeadás az R2-beli vektorösszeadás, a szorzás, pedig a
művelet, mely természetesen a "polinomszorzásnak" az előző állításbeli izomorfizmus által létesített képe.
Ez az interpretáció azért fontos, mert explicitté teszi, hogy a C örökli az R2 topológiáját.
Geometriai modell
A szorzással együtt C egységelemes, nullosztómentes algebrát alkot (tehát vektortér és van egy mindkét változójában lineáris belső szorzás, melyben van egység és „nullával nem lehet osztani”). Felmerülhet a gyanúnk, hogy talán reprezentálhatjuk a komplex számokat a 2×2-es valós mátrixon M2×2 (R) algebrájának egy részalgebrájaként. Ezt a komplex számok trigonometrikus alakja segítségével tehetjük meg. Ismert, hogy a komplex számmal való szorzás forgatva nyújtás, azaz lineáris leképezés az R2 síkon:
Világos, hogy ekkor az a + bi kanonikus alakot használva a komplex számoknak megfelelő mátrixok halmaza:
Ez a mátrixhalmaz kétdimenziós altér az M2×2 (R) algebrában, melyet például a közvetve onnan is láthatjuk, hogy forgatva nyújtások is alteret alkotnak a lineáris leképezések terében.
C topológiája
R2 gömbi környezetei lesznek C gömbi környezetei. Általában, minden topologikus fogalom C-ben R2-re vezetünk vissza. Tehát, adott r > 0 valós számra és z0 ∈ C számra:
az r sugarú z0 középpontú nyílt gömbi környezet. Itt a | . | abszolútérték helyett, mely a || . ||2 euklideszi norma, elvileg R2 bármelyik normája alkalmas lenne, hisz véges dimenziós normált térben minden norma ekvivalens, azaz ugyanazokat a nyílt halmazokat határozzák meg. Szokásos módon értelmezettek az előbb említett nyílt halmazok is. Ω ⊆ C nyílt, ha minden pontjával együtt, annak egy nyílt gömbi környezetét is tartalmazza:
Egy A ⊆ C halmaz belsején értjük azon pontok halmazát, melyeknek egy egész gömbi környezete benne van A-ban
Mivel R2-ben minden norma ekvivalens (ugyanazokat a nyílt halmazokat határozzák meg), ezért adott feladatokban tetszőleges, a feladathoz jól illeszkedő normát választhatunk. Topologikus szempontokból a komplex és R2-R2 függvények között a következő azonosítással élhetünk. Ha f: C⊇  C függvény, akkor z = x + iy, f(z)=u(x,y)+iv(x,y), ill.
C függvény, akkor z = x + iy, f(z)=u(x,y)+iv(x,y), ill.
Folytonosság
Azt mondjuk, hogy az A ⊆ C halmazon értelmezett f függvény folytonos a z ∈ A pontban, ha z-ben f folytonos mint R2 ⊇ A  R2 függvény. Maga az f folytonos, ha az értelmezési tartománya minden pontjában folytonos.
R2 függvény. Maga az f folytonos, ha az értelmezési tartománya minden pontjában folytonos.
A többváltozós valós analízisből ismert tény miatt fennáll:
Állítás. Az f komplex függvény pontosan akkor folytonos az értelmezési tartománya egy pontjában, ha ott a függvény valós és képzetes része, mint kétváltozós valós függvény folytonos. Azaz, ha f-et a következő alakban írjuk:
ahol u és v valós értékű függvények (rendre Re(f) és Im(f)), továbbá z0 = x0 + iy0 ∈ Dom(f), akkor a következők ekvivalensek:
- f folytonos a z0-ban
- u és v függvények folytonosak az (x0,y0)-ban
A kétváltozós függvények közötti határérték-folytonosság kapcsolat is megfogalmazható komplex módon. Itt az f = u + vi függvény határértékén a z = x + iy pontban a limx u + i limy v szám adja. Ekkor
Állítás. Az f komplex függvény pontosan akkor folytonos az értelmezési tartománya egy belső pontjában, ha ott a függvénynek létezik határértéke és az a helyettesítési érték.
A komplex függvények folytonosságának egyik, de nem egyetlen feltétele az, hogy az (u,v) reprezentáció R2-ben lineáris legyen, hiszen a véges dimenziós normált terek között ható lineáris leképezések folytonosak. A nem-folytonosságnál érdemes a határérték nem létezését vizsgálni, hátha ez célra vezet.
Feladat. Legyen w ∈ C. Igazoljuk, hogy az alábbi függvények folytonosak!
Megoldás.
Az 1. az R2-ben eltolás a w-nek megfelelő vektorral (Re(w), Im(w))-vel, így affin leképezés, ami folytonos.
2. a w mátrixreprezentációjának megfelelő mátrixszal való szorzás, azaz lineáris leképezés, s így folytonos.
3. azaz a konjugálás: (x,y)  (x,–y) a valós tengelyre való tükrözés, ami szintén lineáris.
(x,–y) a valós tengelyre való tükrözés, ami szintén lineáris.
Végül a reciprok:
így, mint R2 ⊃ R2 függvény:
R2 függvény:
amely olyan, hogy mindkét komponensfüggvénye folytonos valós függvényekből van összeállítva a folytonosságot megőrző módon, azaz az értelmezési tartománya minden pontjában folytonos.
Feladat. Folytonos-e a z = 0-ban az
Megoldás.
Ha z = x + iy és (x,y) ≠ (0,0), akkor:
A komponensfüggvények felírhatók egy 0-hoz tartó és egy korlátos függvény szorzataként:
és
így (x,y) (0,0) esetén a 0-hoz tartanak, így a függvény maga a (0,0)-hoz, azaz a komplex 0-hoz. Mivel itt a függvény értéke 0, ezért f a 0-ban folytonos.
(0,0) esetén a 0-hoz tartanak, így a függvény maga a (0,0)-hoz, azaz a komplex 0-hoz. Mivel itt a függvény értéke 0, ezért f a 0-ban folytonos.
Ha folytonos komplex függvényekből alapműveletek segítségével alkottunk függvényeket, akkor azok is folytonosak maradnak, mert a megfelelő R2-beli függvények ekkor olyanok lesznek, melyek mindegyik komponensfüggvénye a valós alapműveletek segítségével vannak definiálva. Ám, ezek megőrzik a folytonosságot.
Állítás. Ha f és g komplex függvények és az z0 pontban (mindketten értelmezettek és) folytonosak, akkor
- f + g
- f
 g
g
-
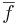
- g(z0) ≠ 0 esetén f/g
is folytonos z0-ban.
Folytonos függvények kompozíciója is folytonos (az kompozíció értelmezési tartományán).
Komplex számkör unicitása
C, azaz a komplex számok teste kétdimenziós valós vektortér. C elemei reprezentálhatók az R2 síkon, a következő megfeleltetésekkel:
a vektortérműveletek pedig:
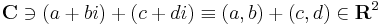 vektorösszeadás (a, b, c, d ∈ R)
vektorösszeadás (a, b, c, d ∈ R)
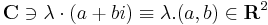 valós számmal való szorzás (λ, a, b ∈ R)
valós számmal való szorzás (λ, a, b ∈ R)
A komplex számok körét a komplex szorzás tulajdonságai egyértelműsítik. C nem csak kétdimenziós valós vektortér, de a szorzással algebra is, sőt C az egyetlen kétdimenziós kommutatív, nullosztómentes valós algebra -- izomorfizmus erejéig. Sok megjelenési formája lehet a komplex számoknak, de bármely két reprezentáció olyan, hogy található olyan kölcsönösen egyértelmű leképezés köztük, mely lineáris és megtartja a szorzást is (azaz algebra izomorfizmus).
A nullosztómentesség és a kommutativitás jellemzően a mátrixalgebrákban nemtriviális tulajdonság. A komplex számok olyan lineáris leképezéseknek felelnek meg, melyek mátrixa
A komplex számok szorzása itt a mátrixszorzás.
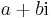
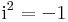
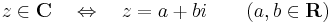
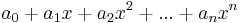
![\mathbf{C}=_{\mathrm{def}}\mathbf{R}[X]/(x^2+1)](/upload/math/d/3/6/d361c86f4c4cc3f09273ef5ab65b6197.png)