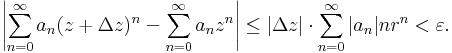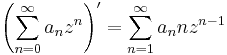Matematika A3a 2008/4. gyakorlat
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) a |
||
| 1. sor: | 1. sor: | ||
''<sub><[[Matematika A3a 2008]]</sub>'' | ''<sub><[[Matematika A3a 2008]]</sub>'' | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Komplex sorozatok== | ==Komplex sorozatok== | ||
Minthogy '''C''' ≡ '''R'''<sup>2</sup> (mint normált vektortér), a komplex sorozatok azon tulajdonságai, melyek a vektortérműveletekkel és az | . | ≡ || . ||<sub>2</sub> euklideszi normával kapcsolatosak mind '''R'''<sup>2</sup>-ből ismertnek tekinthetők. A sorozatok konvergenciáját ugyanúgy definiáljuk, mint '''R'''<sup>2</sup>-ben: | Minthogy '''C''' ≡ '''R'''<sup>2</sup> (mint normált vektortér), a komplex sorozatok azon tulajdonságai, melyek a vektortérműveletekkel és az | . | ≡ || . ||<sub>2</sub> euklideszi normával kapcsolatosak mind '''R'''<sup>2</sup>-ből ismertnek tekinthetők. A sorozatok konvergenciáját ugyanúgy definiáljuk, mint '''R'''<sup>2</sup>-ben: | ||
A lap 2013. szeptember 15., 11:24-kori változata
Tartalomjegyzék |
Komplex sorozatok
Minthogy C ≡ R2 (mint normált vektortér), a komplex sorozatok azon tulajdonságai, melyek a vektortérműveletekkel és az | . | ≡ || . ||2 euklideszi normával kapcsolatosak mind R2-ből ismertnek tekinthetők. A sorozatok konvergenciáját ugyanúgy definiáljuk, mint R2-ben:
Ekkor a fenti z egyértelmű, és ez a sorozat határértéke (lim(zn))
A legfontosabb jellemzése tehát a konvergenciának az R2-ből kölcsönzött, a komponensekre vonatkozó kritérium:
Tétel – A C-beli (zn) = (an + ibn) sorozat konvergens akkor és csak akkor, ha
- (an) konvergens és
- (bn) konvergens.
Ekkor lim(zn) = lim(an) + i lim(bn)
lim(bn)
Fontos látni a kapcsolatot a sorozathatárék és a függvényhatárérték között. Egy (ζn) komplex sorozat nem más, mint egy
függvény. Ha Z-t komplex részhalmaznak gondoljuk (ahogy az is), akkor az egyetlen torlódási pontja a ∞. Ezért egy sorozatnak pontosan akkor létezik határértéke és ez a w szám, ha mint függvénynek létezik határértéke és az a w. Azaz:
Ebből következik, hogy a függvényhatárértékre vonatkozó minden műveleti szabály öröklődik a sorozathatárértékre.
Nullsorozatok
A 0 komplex számhoz tartó sorozatok nullsorozatok. Az abszolútérték és a szorzás jó tulajdonságai miatt öröklődnek a valós sorozatok alábbi tulajdonságai.
Állítás – Legyen (zn) komplex számsorozat.
- abszolútérték: zn
 0 akkor és csak akkor, ha |zn|
0 akkor és csak akkor, ha |zn|  0
0
- eltolás: zn
 z akkor és csak akkor, ha (zn – z)
z akkor és csak akkor, ha (zn – z)  0
0
- "K
 0": ha (wn) korlátos és zn
0": ha (wn) korlátos és zn  0, akkor (wn
0, akkor (wn  zn)
zn)  0
0
- majoráns: ha (δn)
 0 valós és |zn| < δn, akkor zn
0 valós és |zn| < δn, akkor zn  0
0
- hányadoskritérium: ha
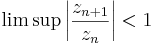 , akkor zn
, akkor zn  0
0
- gyökkritérium: ha
![\limsup\sqrt[n]{|z_n|}<1\,](/upload/math/c/1/a/c1a8b8217114281734effeccc096c4c5.png) , akkor zn
, akkor zn  0
0
Ezek közül C-ben a legjellegzetesebb a "K  0", hiszen ez azt állítja, hogy nem csak a λn.zn skalárral történő szorzás esetén igaz a "korlátos - nullához" tartó kritérium (mindkét változóban), hanem komplex szorzás is ilyen.
0", hiszen ez azt állítja, hogy nem csak a λn.zn skalárral történő szorzás esetén igaz a "korlátos - nullához" tartó kritérium (mindkét változóban), hanem komplex szorzás is ilyen.
1. Feladat
(Útmutatás: hivatkozzunk a "korlátos szor nullához tartó" kritériumra.)
2. Feladat.
ahol az n-edik gyök a valós számból vont valós gyök.
(Útmutatás: "i-telenítsük" a nevezőt.)
ugyanis
3. Feladat.
(Útmutatás: használjunk trigonometrikus alakot és hatványozzunk.)
Mert a szögfüggvények argumentumában lévő sorozat az 1-hez tart (pl L'Hospital-szabállyal majd átviteli elvvel ellenőrizhető), a első szorzó pedig az 1-ehez tart (rendőrelvvel). Az argumentumokban lévő értéket tertmészetesen radiánban kell venni: nem 1˚, hanem 1 rad.
Komplex sorok
Minden normált térben definiálhatók sorok és ezek konvergenciája, így C-ben is. Az (zn) sorozat
részletösszegeinek (sn) sorozatát a (zn) -ből képzett sornak nevezzük és ∑(zn)-nel jelöljük. Azt mondjuk, hogy a ∑(zn) sor konvergens és összege a w komplex szám, ha (zn) részletösszegeinek sorozata konvergens és határértéke w. Ekkor az összeget a
szimbólummal jelöljük.
Komponensek
Az egyik módja, hogy a komplex sorok konvergenciáját visszavezessük a valósokra, ha a komponenssorozatokat vesszük:
esetén az összegeket elképzelve, azokból az i kiemelhető, így
ahol az összeget és a szorzást tagonként végezzük. Ekkor egy sor ponrosan akkor konvergens, ha mindkét komponense konvergens.
Cauchy-kritérium és abszolút konvergencia
Világos, hogy egy sor, mint részletösszegsorozat pontosan akkor konvergens, ha Cauchy-sorozat. Ez a Cauchy-kritérium sorokra.
Létezik az abszolút konvergencia fogalmai is. Egy sor abszolút konvergens, ha a tagjai abszolútértékéből képezett sorozat konvergens. Igaz az, hogy egy normált tér akkor és csak akkor teljes, ha minden abszolút konvergens sor konvergens benne. (És C teljes, mert minden Cauchy-sorozat konvergál benne, ami pont annak a módja, hogy belássuk az előbbi kritériumot.) Persze az előfordul a teljes terekben is, hogy konvergens sorozatok nem lesznek abszolút konvergensek.
Kritériumok az abszolút konvergenciára
Az abszolút konvergencia fenti kritériumából egy sor komplex sorokra vonatkozó kritérium adódik a valósból.
Tétel – Legyen (zn) komplex számsorozat.
- Szükséges kritérium: Ha ∑(zn) konvergens, akkor (zn) nulsorozat.
- Geometriai sor: ha |z| < 1, akkor
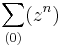 konvergens és az összege:
konvergens és az összege:
- Összehasonlító kritérium: ha az ∑(rn) valós sor konvergens és |zn| ≤ rn majdnem minden n-re, akkor ∑(zn) abszolút konvergens (majoráns-kritérium). Ha az ∑(rn) pozitív valós sor divergens és rn ≤ |zn| m.m., akkor ∑(zn) divergens (minoráns-kritérium).
- p-edik hatvány próba: ha p > 1 valós, akkor a
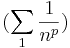 valós sor konvergens.
valós sor konvergens.
- Ha 0 ≤ p ≤ 1, akkor a
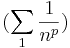 valós sor divergens.
valós sor divergens.
- Ha 0 ≤ p ≤ 1, akkor a
- Hányadoskritérium: ha
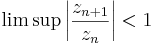 , akkor ∑(zn) abszolút konvergens. Ha a "liminf" > 1, akkor divergens
, akkor ∑(zn) abszolút konvergens. Ha a "liminf" > 1, akkor divergens
- Gyökkritérium: ha
![\limsup\sqrt[n]{|z_n|}<1\,](/upload/math/c/1/a/c1a8b8217114281734effeccc096c4c5.png) , akkor ∑(zn) abszolút konvergens. Ha a "limsup" > 1, akkor divergens.
, akkor ∑(zn) abszolút konvergens. Ha a "limsup" > 1, akkor divergens.
Megjegyezzük, hogy ha a gyökök és hányadosok sorozata konvergál, akkor ugyanahhoz a számhoz konvergálnak.
4.
Konvergens-e illetve abszolút konvergens-e?
5.
- Konvergens-e és mi a határértéke:
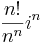
- Konvergens-e
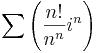
- Milyen z-re konvergens:
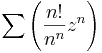
(Útmutatás: használjuk a hányadoskritériumot, vagy vizsgáljuk, hogy milyen rendben tartanak a végtelenhez az összetevősorozatok.)
azaz 0-hoz tart-
6.
- Konvergens-e és mi a határértéke:
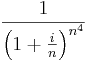
- Konvergens-e
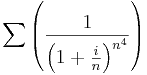
- Milyen z-re konvergens:
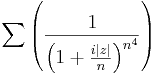
(Útmutatás: használjuk a gyökkritériumot.)
Így a reciproka a 0-hoz tart, azaz a limszup < 1.
Komplex hatványsorok
Definíció – Hatványsor – Legyen (an) komplex számsorozat és z0 ∈ C. Ekkor az ∑(an(idC-z0)n) függvénysort hatványsornak nevezzük és összegét, az
hozzárendelési utasítással értelmezett, a {z ∈ | ∑(an(z-z0)n) konvergál } halmazon értelmezett függvényt a hatványsor összegének nevezzük. Középpontja z0, együtthatósorozata (an).
A továbbiakban csak a ∑(anzn) alakú, azaz a 0 körüli hatványsorokkal foglalkozunk (ezzel nem csorbítjuk az általánosságot, mert eltolással megkaphatjuk a többit is).
Tétel – Cauchy–Hadamard-tétel – Ha (an) komplex számsorozat, ![c= \limsup\limits_{n}\sqrt[n]{|a_n|}](/upload/math/0/8/a/08a549d611fba6d99576372e981e8b49.png) és
és
akkor ∑(anzn) abszolút konvergens a BR(0) gömbön és divergens a B1/R(∞) gömbön.
A tétel minden részletre kiterjedő bizonyítását nem végezzük el, csak utalunk rá, hogy nyilvánvaló, hogy a Cauchy-féle gyökkritériumot kell benne használni. A tételbeli R sugarat a hatványsor konvergenciasugarának nevezzük. R-et másként is kiszámíthajuk. Ha azt tudjuk, a hányadoskritérium alapján, hogy
akkor létezik és ezzel egyenlő az n-edik gyökök sorozata is:
ahol az idézőjel azt jelzi, hogy a konvergenciasugár lehet végtelen vagy 0 is.
7. Feladat. Mi az alábbi hatványsorok konvergenciaköre és -sugara?
Analitikusnak nevezünk egy f komplex függvényt, a z0 pontban, ha van olyan δ sugarú környezet és ∑(an(z-z0)n) hatványsor, hogy minden z ∈ Bδ(z0)-ra f érelmezett, ∑(an(z-z0)n) konvergens és
Ezt úgy jelöljük, hogy f ∈ Cω(z0).
8. Feladat
- Van-e olyan
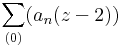 hatványsor, mely konvergál a 0-ban, de divergál a 3-ban. Konvergál 2-ben, de divergál az 2,000001-ben?
hatványsor, mely konvergál a 0-ban, de divergál a 3-ban. Konvergál 2-ben, de divergál az 2,000001-ben?
- Igazoljuk, hogy az alábbi függvény analitikus a nullában. Mi sorfejtés a konvergenciaköre?
Hatványsorok összegfüggvényének folytonossága és differenciálhatósága
Tétel – Ha (an) komplex számsorozat, akkor az ∑(anzn) hatványsor összegfüggvénye folytonos a konvergenciakör belsejében. Sőt, reguláris is ott.
Emlékeztetünk arra, hogy egy függvény reguláris egy pontban, ha a pont egy környezetében mindenütt értelmezett és komplex deriválható. A tétel szerint tehát analitikus függvény reguláris. A döbbenetes azonban, hogymint később kiderül: reguláris függvény analitikus: f ∈ Cω(z0) akkor és csak akkr, ha f ∈ Reg(z0).
Bizonyítás. Legyen z a konvergenciakör egy belső pontja és Δz olyan, hogy még z + Δz is a konvergenciakör belsejébe esik. Ekkor:
mert mindkét sor konvergens, ekkor algebrai azonosságokkal:
vagy ha tetszik nemnulla Δz-vel:
a jobb oldalon álló sor konvergenciáját a gyökkritériummal láthatjuk be:
ahol r olyan pozitív szám, hogy | z + Δz | < r < R (ez utóbbi a hatványsor konvergenciasugára). És
Így azt kaptuk, hogy minden olyan Δz-re, melyre | z + Δz | < r, teljesül és |Δz| <ε/(1+∑n|an|nrn)=:δ
Hosszadalmasabb számolásokkal, de lényegében ugyanígy kimutatható, hogy a hatványsor összegfüggvénye komplex differenciálható is a konvergenciakör belsejében és deriváltja a formális tagonkénti deriválásal kapott sor összegfüggvényével egyenlő, tehát:
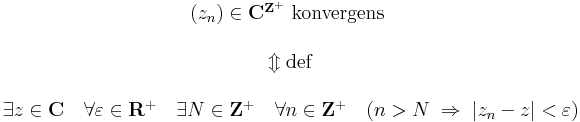
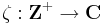
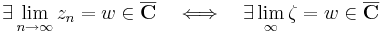
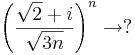
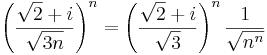
![\frac{\sqrt[n]{n^3+2n}}{i+1}\to ?](/upload/math/6/8/6/686b4f1dcc2e39ef2d30b890a1e8b99e.png)
![\frac{\sqrt[n]{n^3+2n}}{i+1}=\frac{(i-1)\sqrt[n]{n^3+2n}}{-1-1}=\frac{i\sqrt[n]{n^3+2n}-\sqrt[n]{n^3+2n}}{-2}\to \frac{1}{2}-\frac{1}{2}i](/upload/math/e/d/6/ed6bf5f9f7eb97cbe95dc9043cdf3ec6.png)
![1\leftarrow\sqrt[n]{n}^3=\sqrt[n]{n^3}\leq\sqrt[n]{n^3+2n}\leq\sqrt[n]{n^3+\frac{n^3}{2}}=\sqrt[n]{\frac{3}{2}n^3}=\sqrt[n]{\frac{3}{2}}\sqrt[n]{n}^3\to 1](/upload/math/f/3/d/f3d3d9b03a73cdf5affda73cd55f7a2a.png)
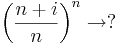
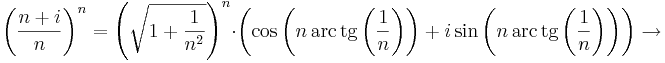
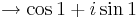
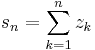
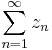
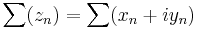
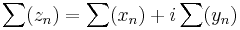
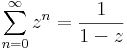
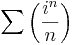
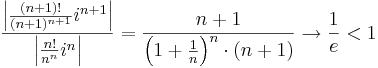
![\sqrt[n]{\left|1+\frac{i}{n}\right|^{n^4}}=\left|1+\frac{i}{n}\right|^{n^3}=\left(\sqrt{\left(1+\frac{1}{n^2}\right)^{n^2}}\right)^n\geq (1+\varepsilon)^n\to +\infty](/upload/math/3/f/0/3f0577419156648cce30f006027bd6ec.png)
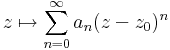
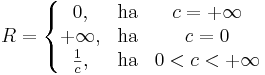
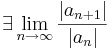
![\exists\lim\limits_{n\to \infty}\sqrt[n]{|a_n|}=\lim\limits_{n\to \infty}\frac{|a_{n+1}|}{|a_n|}=\,''\,\frac{1}{R}\,''](/upload/math/2/1/0/210b8f12a11f0846e6103b096dee2a3d.png)
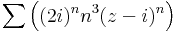
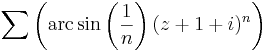
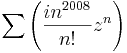
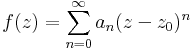
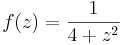
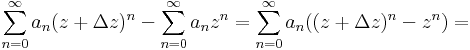
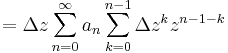
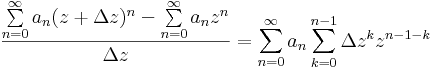
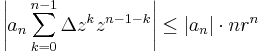
![\limsup\limits_{n\to \infty}\sqrt[n]{|a_n|\cdot n r^n}=\limsup\limits_{n\to \infty}\sqrt[n]{|a_n|}\cdot 1 \cdot r\leq\frac{1}{R}r<1\,](/upload/math/e/f/0/ef0679b874a4aae352293176852288ad.png)