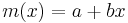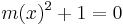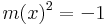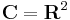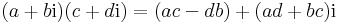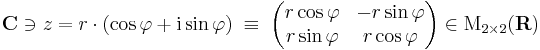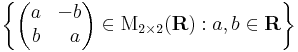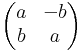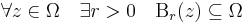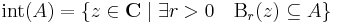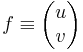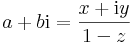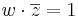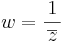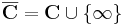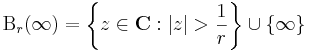Matematika A3a 2008/4. gyakorlat
Mozo (vitalap | szerkesztései) (→C kompaktifikálása) |
Mozo (vitalap | szerkesztései) |
||
| 124. sor: | 124. sor: | ||
Ha '''C'''U{∞}-t lefedi egy nyílt halmazrendszer, akkor ∞-t is lefedi belőlük egy, mondjuk ''U''. ''U'' lefedi az ∞ egy gömbi környezetét, mondjuk B<sub>r</sub>(∞)-t. Elegendő tehát tekintenünk '''C'''U{∞} lefedéséhez a halmazrendszerből az ''U''-t és a B<sub>r</sub>(∞) komplementerét lefedő halmazokat. De ez utóbbiakból véges sok is van melyek még mindig lefedik, mert B<sub>r</sub>(∞) komplemetere a 0 középponttú 1/r sugarú zárt körlap, mely kompakt. | Ha '''C'''U{∞}-t lefedi egy nyílt halmazrendszer, akkor ∞-t is lefedi belőlük egy, mondjuk ''U''. ''U'' lefedi az ∞ egy gömbi környezetét, mondjuk B<sub>r</sub>(∞)-t. Elegendő tehát tekintenünk '''C'''U{∞} lefedéséhez a halmazrendszerből az ''U''-t és a B<sub>r</sub>(∞) komplementerét lefedő halmazokat. De ez utóbbiakból véges sok is van melyek még mindig lefedik, mert B<sub>r</sub>(∞) komplemetere a 0 középponttú 1/r sugarú zárt körlap, mely kompakt. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Kategória:Matematika A3]] | [[Kategória:Matematika A3]] | ||
A lap 2013. október 6., 21:14-kori változata
Tartalomjegyzék |
Komplex számkör és reprezentációi
A komplex számok C halmazát és műveleteit legalább három, lényegesen más szemszögből lehet láttatni. A meghatározottság kedvéért összefoglaljuk a komplex számok legfontosabb algebrai tulajdonságait. Nem térünk ki minden egyes műveleti tulajdonságra, ezek megtalálhatók a komplex számok algebráját leíró tankönyvekben.
Algebrai modell
A komplex számok olyan
alakú formális kifejezések, ahol a és b valós számok, i pedig azzal a speciális tulajdonsággal rendelkezik, hogy
A komplex számok halmazát a C szimbólummal jelöljük, tehát
itt a-t a z valós részének nevezzük és Re(z)-vel jelöljük, b-t a z képzetes részének nevezzük és Im(z)-vel jelöljük. Világos, hogy Im(z) ∈ R, azaz "tiszta" valós.
Megjegyzés. A kevéssé informatív "formális kifejezés" helyett bevezethetjük a komplex számokat valódi algebrai objektumokként. A komplex számok halmazát egy a maradékos osztással rendelkező halmazból konstrulájuk: a valós együtthatós polinomok R[X] halmazából. Közismert, hogy a valósegyütthatós, egyhatározatlanú polinomokal, azaz a
alakú kifejezésekkel, ahol az ai-k valós számok, n pedig nemnegatív egész, lehet maradékosan osztani (polinomosztás). Ekkor
azaz a komplex számok halmaza a valósegyütthatós polinomok x2+1 polinommal történő osztási maradékai. Világos, hogy minden ilyen maradék előáll
alakban, azaz legfeljebb elsőfokú polinom alakjában. Ebben a számkörben az összeadás a polinomösszeadás, a szorzás a polinomok szorzása (illetve ezen eredményének x2+1-vel történő osztási maradéka). Amikor két elsőfokú polinom szorzata másodfokú, akkor sem lépünk ki a számkörből, hisz a
polinomegyenlet megoldható, éspedig az m(x)=x polinom (az identitás) megoldás. Ekkor
azaz ebben a számkörben létezik a -1-nek négyzetgyöke. Az m(x)=x polinom az, mely az i egység szerepét játssza és így is jelöljük ezt ezentúl.
Akárcsak a legfeljebb elsőfokú a + bx alakú polinomok esetén, a C-t alkotó formális kifejezések között is értelmezhetjük az összeadást és a szorzást. Ezeket pontosan úgy definiáljuk, mint az a + bx alakú polinomok összegét és szorzatát, azzal a specialitással, hogy ahol a polinomok a szorzást követően másodfokúvá válnak, ott a komplex számok az i2=-1 egyenlőség miatt visszaérkeznek az a + bi alakú kifejezések körébe. Ezért lesz C zárt arra a szorzásra, amit a polinomok mintájára definiálunk.
Már innen is látszik, hogy a komplex számok halmaza kétdimenziós valós test feletti vektortér. Kimondhatjuk tehát:
Állítás. A C számkör a komplex számok
- (a+bi) + (c+di) = (a+c) + (b+d)i összeadásával és a
- λ(a+bi) = λa + λbi, a λ valós számmal való szorzással
kétdimenziós valós vektorteret alkotnak és így lineárisan izomorfak a valós számpárok R2 vektorterével.
Halmazelméleti modell
Az algebrai modellben nem teljesen világos, hogy mi is az i elem. Az előző állítás azonban lehetőséget biztosít arra, hogy konkrétan megadjuk a komplex számok halmazát mindenféle olyan kifejezés használata nélkül, mint "formális kifejezés" stb. (Valójában persze az algebrai modell is jól értelmezett módon adja meg a komplex számok halmazát, ha az a + bi alakú formális kifejezéseken az R[X] polinomgyűrűnek az (1+X2) polinommal történő maradékos osztásának maradékait értjük).
A számpár reprezentációban:
az összeadás az R2-beli vektorösszeadás, a szorzás, pedig a
művelet, mely természetesen a "polinomszorzásnak" az előző állításbeli izomorfizmus által létesített képe.
Ez az interpretáció azért fontos, mert explicitté teszi, hogy a C örökli az R2 topológiáját.
Geometriai modell
A szorzással együtt C egységelemes, nullosztómentes algebrát alkot (tehát vektortér és van egy mindkét változójában lineáris belső szorzás, melyben van egység és „nullával nem lehet osztani”). Felmerülhet a gyanúnk, hogy talán reprezentálhatjuk a komplex számokat a 2×2-es valós mátrixon M2×2 (R) algebrájának egy részalgebrájaként. Ezt a komplex számok trigonometrikus alakja segítségével tehetjük meg. Ismert, hogy a komplex számmal való szorzás forgatva nyújtás, azaz lineáris leképezés az R2 síkon:
Világos, hogy ekkor az a + bi kanonikus alakot használva a komplex számoknak megfelelő mátrixok halmaza:
Ez a mátrixhalmaz kétdimenziós altér az M2×2 (R) algebrában, melyet például a közvetve onnan is láthatjuk, hogy forgatva nyújtások is alteret alkotnak a lineáris leképezések terében.
Komplex számkör unicitása
C, azaz a komplex számok teste kétdimenziós valós vektortér. C elemei reprezentálhatók az R2 síkon, a következő megfeleltetésekkel:
a vektortérműveletek pedig:
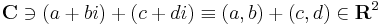 vektorösszeadás (a, b, c, d ∈ R)
vektorösszeadás (a, b, c, d ∈ R)
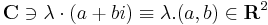 valós számmal való szorzás (λ, a, b ∈ R)
valós számmal való szorzás (λ, a, b ∈ R)
A komplex számok körét a komplex szorzás tulajdonságai egyértelműsítik. C nem csak kétdimenziós valós vektortér, de a szorzással algebra is, sőt C az egyetlen kétdimenziós kommutatív, nullosztómentes valós algebra -- izomorfizmus erejéig. Sok megjelenési formája lehet a komplex számoknak, de bármely két reprezentáció olyan, hogy található olyan kölcsönösen egyértelmű leképezés köztük, mely lineáris és megtartja a szorzást is (azaz algebra izomorfizmus).
A nullosztómentesség és a kommutativitás jellemzően a mátrixalgebrákban nemtriviális tulajdonság. A komplex számok olyan lineáris leképezéseknek felelnek meg, melyek mátrixa
A komplex számok szorzása itt a mátrixszorzás.
C topológiája
R2 gömbi környezetei lesznek C gömbi környezetei. Általában, minden topologikus fogalom C-ben R2-re vezetünk vissza. Tehát, adott r > 0 valós számra és z0 ∈ C számra:
az r sugarú z0 középpontú nyílt gömbi környezet. Itt a | . | abszolútérték helyett, mely a || . ||2 euklideszi norma, elvileg R2 bármelyik normája alkalmas lenne, hisz véges dimenziós normált térben minden norma ekvivalens, azaz ugyanazokat a nyílt halmazokat határozzák meg. Szokásos módon értelmezettek az előbb említett nyílt halmazok is. Ω ⊆ C nyílt, ha minden pontjával együtt, annak egy nyílt gömbi környezetét is tartalmazza:
Egy A ⊆ C halmaz belsején értjük azon pontok halmazát, melyeknek egy egész gömbi környezete benne van A-ban
Mivel R2-ben minden norma ekvivalens (ugyanazokat a nyílt halmazokat határozzák meg), ezért adott feladatokban tetszőleges, a feladathoz jól illeszkedő normát választhatunk. Topologikus szempontokból a komplex és R2-R2 függvények között a következő azonosítással élhetünk. Ha f: C⊇  C függvény, akkor z = x + iy, f(z)=u(x,y)+iv(x,y), ill.
C függvény, akkor z = x + iy, f(z)=u(x,y)+iv(x,y), ill.
C kompaktifikálása
Kompakt egy K halmaz, ha teljesül rá, hogy akárhogy is fedjük le nyílt halmazok rendszerével, azok közül már véges sok halmaz is lefedi a K-t. Szimbolikusan:
- K kompakt, ha minden (Ωi)i∈I halmazrendszerhez, melyre
- Ωi nyílt minden i∈I-re és
- K ⊆ U(Ωi)i∈I
- létezik J ⊆ I véges indexhalmaz, hogy K ⊆ U(Ωi)i∈J
RN-ben egy halmaz pontosan akkor kompakt, ha korlátos és zárt. Tehát maga C nem kompakt, hisz nem korlátos (bár zárt). Viszont C egyetlen egy ponttal kibővítve már kompakttá tehető, ugyanis egy ideális pont hozzávételével C kölcsönösen egyértelmű és folytonos kapcsolatba hozható a gömbfelülettel, mely R3-ban kompakt. Ezt a sztereografikus projekcióval oldjuk meg.
A Riemann-gömb konstrukciójához vegyük az R3-ban az origó középponttú egységgömböt és gondoljunk úgy az [xy] síkra, mint a C komplex számsíkra. Az egységgömb pontjait a következő módon feleltetjük meg a komplex számoknak. Tekintsük a gömbön a (0,0,1) koordinátájú P pólust és egy a + bi komplex szám esetén az (a,b,0) pontot kössük össze P-vel egy e egyenes által. Ekkor az e egyetlen pontban metszi az egységgömböt, mely kijelöli az a + bi-nek megfelelő pontot. Ha az a + bi-nek megfeleltetett Riemann-gömbfelületbeli pont koordinátái (x,y,z), akkor ezek kapcsolata:
Megjegyzés. Ismerős geometriai leképezésre bukkanhatunk, ha a Riemann-gömbfelület egy (x,y,h) és (x,y,-h) pontjának megfelelő komplex számnak a kapcsolatát írjuk fel. Legyen ugyanis
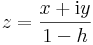 és
és 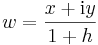
Ekkor a z konjugáltját a w-vel összeszorozva azt kapjuk, hogy:
Amiből az következik, hogy a végpontok origótól vett távolságának a szorzata 1, azaz 1 a két szám hosszának mértani közepe. Ez viszont azt jelenti, hogy w nem más, mint a z inverziója az egységkörre vonakozóan és az inverziót kifejező komplex függvény a
leképezés. Eszerint a reciprok-konjugált (de a reciprok is) egy origón át nem menő kört körbe, az origón átmenő kört egyenesbe, egy origón át nem haladó egyenes egy origón átmenő körbe és egy origón áthaladó egyenest saját magába képezi.
Ha tehát a C-hez hozzáveszünk egy ∞-nel jelölt objektumot, és ennek megfeleltetjük a P pólust, akkor a
halmaz kölcsönösen egyértelmű megfeleltetésbe hozható a Riemann-gömbfelülettel. Ahhoz, hogy ennek folytonosságáról beszélhessünk, definiálnunk kell ∞ gömbi környezeteit. Ezek a következő alakú halmazok lesznek:
ahol r > 0.
Feladat. Igazoljuk, hogy CU{∞} kompakt (toplologikusan, ill. gyakorlásképpen sorozatkompakt)!
(Útmutatás: az elsőhöz az origó körüli zárt gömbök kompaktságát, a másodikhoz a Bolzano-Weierstrass-féle kiválasztási tételt kell használni (persze korlátos sorozatra).)
Ha CU{∞}-t lefedi egy nyílt halmazrendszer, akkor ∞-t is lefedi belőlük egy, mondjuk U. U lefedi az ∞ egy gömbi környezetét, mondjuk Br(∞)-t. Elegendő tehát tekintenünk CU{∞} lefedéséhez a halmazrendszerből az U-t és a Br(∞) komplementerét lefedő halmazokat. De ez utóbbiakból véges sok is van melyek még mindig lefedik, mert Br(∞) komplemetere a 0 középponttú 1/r sugarú zárt körlap, mely kompakt.
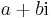
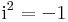
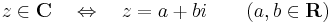
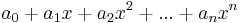
![\mathbf{C}=_{\mathrm{def}}\mathbf{R}[X]/(x^2+1)](/upload/math/d/3/6/d361c86f4c4cc3f09273ef5ab65b6197.png)