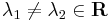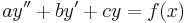Matematika A3a 2008/4. gyakorlat
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Állandó együtthatós lineáris differenciálegyenlet) |
Mozo (vitalap | szerkesztései) |
||
| 14. sor: | 14. sor: | ||
Csak a másodrendű esetet tárgyaljuk: | Csak a másodrendű esetet tárgyaljuk: | ||
:<math>ay''+by'+cy=f(x)\,</math> | :<math>ay''+by'+cy=f(x)\,</math> | ||
| − | ha ''a'', ''b'', ''c'' ∈ '''R'''. Ilyenkor a homogén egyenlet megoldását az ''a''λ<sup>2< | + | ha ''a'', ''b'', ''c'' ∈ '''R'''. Ilyenkor a homogén egyenlet megoldását az ''a''λ<sup>2</sup>+''b''λ+''c''=0 karakterisztikus egyenlet megoldásából származó λ gyökökből száraztatjuk (bizonyítása a bizonyítások között). |
| − | :<math>y(x)=C_1e^{\lambda_1x}+C_2e^{\lambda_2x}</math>, ha <math>\ | + | :<math>y(x)=C_1e^{\lambda_1x}+C_2e^{\lambda_2x}</math>, ha <math>\lambda_1\ne\lambda_2\in\mathbf{R}\,</math> |
A lap 2016. március 4., 22:45-kori változata
Állandó együtthatós lineáris differenciálegyenlet
| 3. gyakorlat |
| 5. gyakorlat |
Csak a másodrendű esetet tárgyaljuk:
ha a, b, c ∈ R. Ilyenkor a homogén egyenlet megoldását az aλ2+bλ+c=0 karakterisztikus egyenlet megoldásából származó λ gyökökből száraztatjuk (bizonyítása a bizonyítások között).
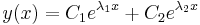 , ha
, ha