Matematika A3a 2008/4. gyakorlat
A MathWikiből
A lap korábbi változatát látod, amilyen Mozo (vitalap | szerkesztései) 2016. március 4., 22:48-kor történt szerkesztése után volt.
Állandó együtthatós lineáris differenciálegyenlet
Csak a másodrendű esetet tárgyaljuk:
ha a, b, c ∈ R. Ilyenkor a homogén egyenlet megoldását az aλ2+bλ+c=0 karakterisztikus egyenlet megoldásából származó λ gyökökből száraztatjuk (bizonyítása a bizonyítások között).
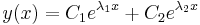 , ha
, ha 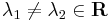
- y(x) = C1eλx + C2xeλx, ha
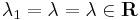 (gyök vagy belső rezonancia esete)
(gyök vagy belső rezonancia esete)
- y(x) = C1eαxcos(βx) + C2eαxsin(βx), ha
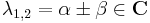
| 3. gyakorlat |
| 5. gyakorlat |