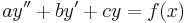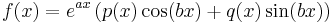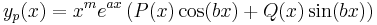Matematika A3a 2008/4. gyakorlat
A MathWikiből
A lap korábbi változatát látod, amilyen Mozo (vitalap | szerkesztései) 2016. március 4., 22:55-kor történt szerkesztése után volt.
Állandó együtthatós lineáris differenciálegyenlet
Csak a másodrendű esetet tárgyaljuk:
ha a, b, c ∈ R.
Ilyenkor a homogén egyenlet megoldását az aλ2+bλ+c=0 karakterisztikus egyenlet megoldásából származó λ gyökökből száraztatjuk (bizonyítása a bizonyítások között).
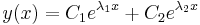 , ha
, ha 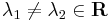
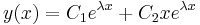 , ha
, ha 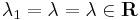 (gyök vagy belső rezonancia esete)
(gyök vagy belső rezonancia esete)
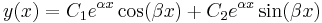 , ha
, ha 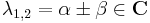
Az inhomogén egyenlet megoldását a következő alakban keressük. Ha az inhomogén tag az alábbi alakban írható
ahol p(x) és q(x) polinomok és a a+ib ∈ C szám m szeres gyöke az aλ2+bλ+c karakterisztikus polinomnak, akkor az yp(x) partikuláris megoldásra a feltevés:
ahol P(x) és Q(x) olyan polinomok, hogy deg P(x)=deg Q(x)= max{deg p(x), deg q(x)}.
Példák
| 3. gyakorlat |
| 5. gyakorlat |