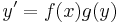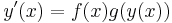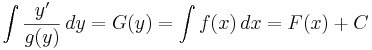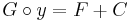Matematika A3a 2008/4. gyakorlat
Tartalomjegyzék |
Szeparábilis differenciálegyenlet
1. Feladat. Milyen függvények elégítik ki az alábbi differenciálegynletet. Van-e olyan, mely a 0-ban 0-t vesz föl, illetve a 0-ban 1-et?
Megoldás. Nyilván a megoldás sehol sem vehet föl nulla értéket, mert akkor
ott nem lenne értelmezve.
A mechanikus megoldási eljárás a következő:
ez az implicit általános megoldás és
az explicit általános megoldás.
A megoldás mechanikus megkeresése után meg kell jegyeznünk, hogy csak olyan intervallumokra kell szorítkoznunk, ahol az y nem ad nullát. Ezeken belül vannak olyan esetek, melyek nem is differenciálhatók a 7. gyök miatt.
(0,1)-en áthaladó megoldás a C = 8/7-es görbe.
Egzisztencia és unicitás
Legyen f : I  R, g: J
R, g: J  R intervallumon értelmezett folytonos függvények, ahol g sehol sem nulla. Ekkor az y: K
R intervallumon értelmezett folytonos függvények, ahol g sehol sem nulla. Ekkor az y: K  J differenciálható függvény, ahol K ⊆ I megoldása az
J differenciálható függvény, ahol K ⊆ I megoldása az
ún. szeparábilis diffegyenletnek, ha minden x ∈ K-ra:
Ekkor a helyettesítéses integrálás szabálya miatt
azaz
ahol G az 1/g egy integrálfüggvénye, F az f-é.
Ennek a függvlnyegyenletnek a differenciálható megoldásai megoldások és ezt nevezzük a diffegyenlet implicit alakban adott általános megoldásának.
Ha G injektív, akkor az explicit általános megoldás globális:
Ha G nem injektív, de van, ahol a deriváltja nem nulla (tehát 1/g nem konstans, azaz g nem konstans, azaz a feladat nem intézhető el primitív függvény kereséssel), és (x0<\sub>, y0) olyan, hogy f(x,y)=G(y)-F(x)-C és G(y0<\sub>)-F(x0<\sub>)-C=0, akkor az inverzfüggvénytétel értelmében van lokális megoldása x0<\sub> körül. Ilyen (x0<\sub>, y0) a C alkalmas beállításával mindig alálható. (Ezt elhisszük.)
Vannak olyan esetek amikor g felveszi a 0-t. Ekkor a fenti sematikus megoldáson kívül egyéb meoldás is felléphet.
2. Feladat. Oldjuk meg az 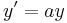 egyenletet.
egyenletet.
Függvényegyenletek
3. Feladat. Van-e nemdifferenciálható megoldása az y^2=x^2\, függvényegynletnek?
4. Feladat. Hány megoldása van az |f(x)|=ex R-en? Hány diffható ebből?
kljklj
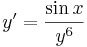
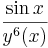
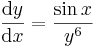
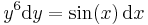
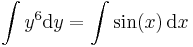
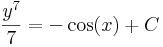
![y(x)=\sqrt[7]{-7\cos(x)+C}\,](/upload/math/e/2/d/e2d7f66e9664a8ea1ef763c670f9b58c.png)