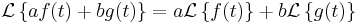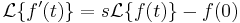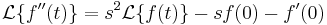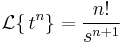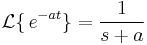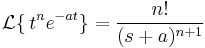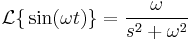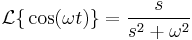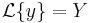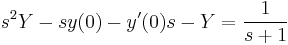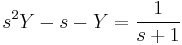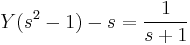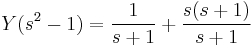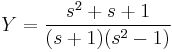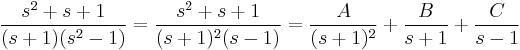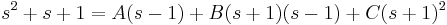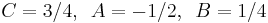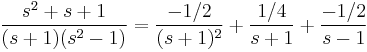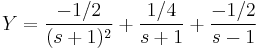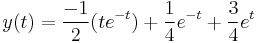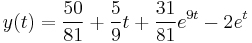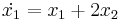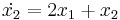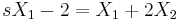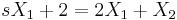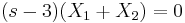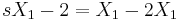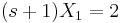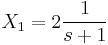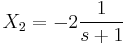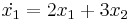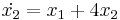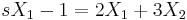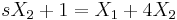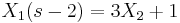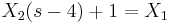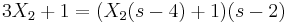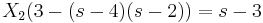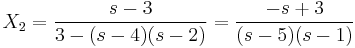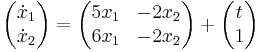Matematika A3a 2008/5. gyakorlat
A MathWikiből
(Változatok közti eltérés)
Mozo (vitalap | szerkesztései) (→Megoldási stratégiák) |
Mozo (vitalap | szerkesztései) (→Megoldási stratégiák) |
||
| 16. sor: | 16. sor: | ||
::állandó együtthatós: | ::állandó együtthatós: | ||
:::kezdeti feltétellel: Laplace-transzformációval | :::kezdeti feltétellel: Laplace-transzformációval | ||
| − | ::::egyenlet másodrendű: | + | ::::egyenlet másodrendű: a<math>y''</math>+by'+cy=h(x), y(0)=... y'(0)=... |
::::egyenletrendszer elsőrendű: y_1, y_2, y_1(0)=... y_2(0)=..., | ::::egyenletrendszer elsőrendű: y_1, y_2, y_1(0)=... y_2(0)=..., | ||
:::általános megoldást keresünk: | :::általános megoldást keresünk: | ||
| − | ::::egyenlet: | + | ::::egyenlet: a<math>y''</math>+by'+cy=h(x) próbafüggvény módszer (böhöm képletek) |
::::egyenletrendszer (nincs kezdeti feltétel, általános megoldást keresünk) A sajátértékei, vektorai | ::::egyenletrendszer (nincs kezdeti feltétel, általános megoldást keresünk) A sajátértékei, vektorai | ||
A lap 2017. november 4., 19:13-kori változata
Tartalomjegyzék |
Megoldási stratégiák
- nemlineáris
- szeparábilis: dy/dx=g(x)/f(y) és f(y)dy=g(x)dx
- szeparábilisra visszavezethető:
- y'=f(ax+by+c) alakú, ilyenkor u=ax+by+c, u'=a+by' vezet célra
- y'=f(y/x) alakú, ilyenkor u=y/x és y'=u'x+u vezet célra
- szeparábilisra visszavezethető:
- egzakt
- egzaktra visszavezethető
- m=m(x)
- m=m(y)
- egzaktra visszavezethető
- szeparábilis: dy/dx=g(x)/f(y) és f(y)dy=g(x)dx
- lineáris
- függvényegyütthatós elsőrendű: y'+f(x)y=h(x). Ekkor az állandó variálásával kell számolni: I., y'+f(x)y=0 megoldása: y=y(x,c) II., y=y(x,c(x)) alakban keressük a megoldást
- állandó együtthatós:
- kezdeti feltétellel: Laplace-transzformációval
- egyenlet másodrendű: ay''+by'+cy=h(x), y(0)=... y'(0)=...
- egyenletrendszer elsőrendű: y_1, y_2, y_1(0)=... y_2(0)=...,
- általános megoldást keresünk:
- egyenlet: ay''+by'+cy=h(x) próbafüggvény módszer (böhöm képletek)
- egyenletrendszer (nincs kezdeti feltétel, általános megoldást keresünk) A sajátértékei, vektorai
- kezdeti feltétellel: Laplace-transzformációval
Laplace-transzformáció
- t, s>0
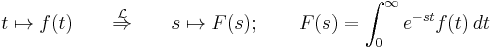
Linearitás
Deriváltak
Elemi függvények
Másodrendű állandó együtthatós inhomogén lineáris kezdetiérték feladat
1.
Mo.
Parciális törtekre bontás:
Innen s=1-gyel 3=4C, s=-1-gyel 1=-2A, és s=0-val 1=-A-B+C. Azaz
2.
Mo.
- L(y') = sY − y(0)
- L(y'') = s2Y − sy(0) − y'(0)
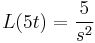
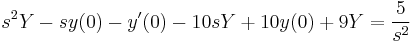
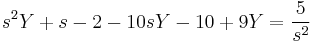
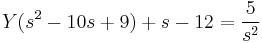
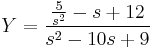
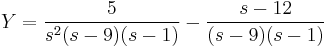
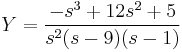
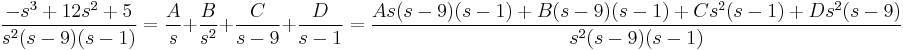
A gyököket beírva: s=0-ra B=5/9
s=1-re D=16/(-8)=-2
s=9-re C.8.81=-243+12.27+5 C=31/81
s=2-re A=50/81
Visszatranszf.
Elsőrendű állandó együtthatós inhomogén lineáris differenciálegyenletrendszer kezdetiérték feltétellel
3.
A  kezdetiérték feltétellel.
kezdetiérték feltétellel.
Mo.
Összeadva őket:
Ami csak akkor teljesülhet minden s-re, ha X2 = − X1. Innen
És végül
- x1(t) = 2e − t
- x2(t) = − 2e − t
4.
A 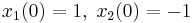 kezdetiérték feltétellel.
kezdetiérték feltétellel.
Mo.
azaz
azaz
...
[5.
]
| 4. gyakorlat |
| 6. gyakorlat |