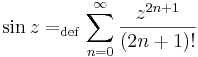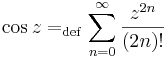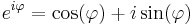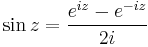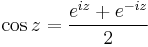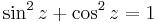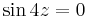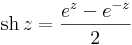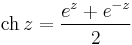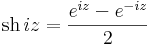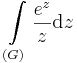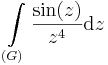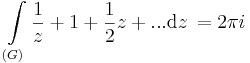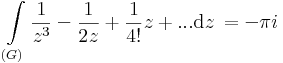Matematika A3a 2008/6. gyakorlat
Mozo (vitalap | szerkesztései) (→Komplex sorozatok) |
Mozo (vitalap | szerkesztései) (→Komplex sorozatok) |
||
| 97. sor: | 97. sor: | ||
''Mo.'' Van neki, ha Δ=0. Ezt ellenőrizni kell, majd az előző módszerrel megkeresi v-t, amivel u+iv reguláris. | ''Mo.'' Van neki, ha Δ=0. Ezt ellenőrizni kell, majd az előző módszerrel megkeresi v-t, amivel u+iv reguláris. | ||
| + | |||
| + | ==Komplex integrál== | ||
| + | |||
| + | ===Görbék a komplex síkon=== | ||
| + | |||
| + | Ha ''G'':[''a'',''b'']<math>\to</math>'''C''', ''t''<math>\mapsto</math>''z''(''t'') folytonosan differenciálható, akkor ''G''-t görbének nevezzük. (Esetleg a folytonos, véges sok helyen nem folytonosan differenciálható előbbi ''G''-ket is görbéknek nevezzük.) A ''G'' görbe ''egyszerű'', ha nem metszi át saját magát, azaz minden <math>t_1</math>, <math>t_2</math>-re, ha <math>z(t_1)=z(t_2)</math>, akkor <math>t_1=t_2</math>. ''G'' zárt, ha <math>z(a)=z(b)</math>. A görbe ''t''-beli irányvektorán a | ||
| + | :<math>\dot{z}(t)=\dot{x}(t)+\mathrm{i}\dot{y}(t)</math> | ||
| + | komplex számot értjük. | ||
| + | |||
| + | ====Példák==== | ||
| + | '''1.''' Legyen ''t''∈[a,b]-re ''z''(''t'') = ''x''(''t'') + i''y''(''t'') olyan, hogy <math>x(t)=x_0+w_1t</math> és <math>y(t)=y_0+w_2t</math>, azaz <math>z(t)=z_0+w t</math>. Ekkor ''z''(''t'') egy egyenes szakasz. | ||
| + | |||
| + | És ekkor: | ||
| + | :<math>\dot{z}(t)=w</math> | ||
| + | '''2.''' Az origó középpontú R sugarú kör: | ||
| + | :<math>z(t)=Re^{\mathrm{i}t}</math> ''t''∈[0,2π] | ||
| + | És ekkor | ||
| + | :<math>\dot{z}(t)=R\mathrm{i}e^{\mathrm{i}t}</math> | ||
| + | hiszen | ||
| + | :<math>\dot{z}(t)=R\dot{\cos(t)+\mathrm{i}\sin(t)}=-R\sin(t)+\mathrm{i}R\cos(t)=\mathrm{i}(R\mathrm{i}\sin(t)+R\cos(t))</math> | ||
| + | ===Komplex vonalmenti integrál=== | ||
| + | '''Definíció.''' Ha ''G'':[a,b]<math>\to</math>'''C''' görbe és f olyan komplex függvény, melyre Ran(G)⊆Dom(f), és f folytonos, akkor belátható, hogy létezik a | ||
| + | |||
| + | :<math>\begin{matrix} | ||
| + | \sum\limits_{i=1}^nf(\zeta_i)\cdot \Delta z_i & \longrightarrow & \int\limits_{G}f(z)\,\mathrm{d}z\\ | ||
| + | & n\to \infty & \\ | ||
| + | & \forall z_i\in G, \;\forall \zeta_i\in \Delta z_i &\\ | ||
| + | & |\Delta z_i|\to 0 & | ||
| + | \end{matrix}</math> | ||
| + | határérték, mely egy speciális Riemann-közelítőösszeg határértéke. Itt a görbén kijelöltük a véges sok <math>z_i</math> pontot, melyek a szigorúan monoton (<math>t_i</math>)-khez tartoznak a <math>z_i=z(t_i)</math> definícióval. Ezen <math>[z(t_i),z(t_{i+1})]</math> görbeszakaszokon belül felvettük tetszőlegesen a ζ<sub>i</sub> közbülső pontokat, és a Δz<sub>i</sub>=<math>[z(t_i),z(t_{i+1})]</math> szakaszokkal elkészítettük az f(ζ<sub>i</sub>)Δz<sub>i</sub> komplex szorzatokat. A határérték ezek görbére vett összegének határértéke. Ez a határérték az f függvény ''G''-re vett komplex integrálja. | ||
| + | |||
| + | '''Visszavezetés valós vonalintegrálra.''' | ||
| + | Az integrál kifejezhető vonalintegrállal. Ha ugyanis f= u + iv, akkor az f=(u,v) vektormezőnek olyan differenciálforma szerinti integrálja a komplex pályamenti integrál, mely az f=(u,v) vektor és a dz=(dx,dy) infinitezimális elmozdulásvektor komplex szorzásaként jön létre: | ||
| + | :<math>\int\limits_{G}f(z)\mathrm{d}z = \int\limits_{G} u\mathrm{d}x-v\mathrm{d }y + i\int\limits_{G} u\mathrm{d}y+v\mathrm{d }x</math> | ||
| + | Ebben a felírásban az (u,-v) és (v,u) olyan segédvektormezők, melyek vonalintegráljai adják meg a komplex integrál valós és képzetes részét. Tehát az integrált a | ||
| + | :<math>\mathbf{P}=\begin{pmatrix}u\\-v\end{pmatrix}</math> és <math>\mathbf{Q}=\begin{pmatrix}v\\u\end{pmatrix}</math> | ||
| + | segédvektormezők síkbeli '''vonalintegráljai''', vagy a | ||
| + | :<math>\mathbf{P}'=\begin{pmatrix}-v\\-u\end{pmatrix}</math> és <math>\mathbf{Q}'=\begin{pmatrix}u\\-v\end{pmatrix}</math> | ||
| + | segédvektormezők síkbeli '''felületi integráljai''' szolgáltatják. | ||
| + | |||
| + | Itt érdemes feleleveníteni, hogy az '''S''' = (<math>s_1</math>, <math>s_2</math>) síkvektormező felületi integrálja nem más, mint a (<math>-s_2</math>, <math>s_1</math>) vektormező vonalintegrálja (a megfelelő irányítással). | ||
| + | |||
| + | :<math>\int\limits_{F} \mathbf{S}\,\mathrm{d}\mathbf{f}=\int\limits_{''F''} s_1 \mathrm{d}y-s_2\mathrm{d}x</math> | ||
| + | megfelelő módon irányítva az F felületet, ill ennek "F" görbe mivoltát. | ||
| + | |||
| + | (Azaz a s_2dx - s_1 dy differenciálforma integrálja. ''Differenciálforma'' -- nemes egyszerűséggel -- egy olyan kifejezése, ahol dx, dy, dz-k és egy vektormező komponensei vannak összeszorozva-összeadva.) | ||
| + | |||
| + | '''Kiszámítási formula.''' Belátható, hogy a fenti integrál a következőkkel egyenlő: | ||
| + | :<math> | ||
| + | \int\limits_{G}f(z)\mathrm{d}z=\int\limits_{a}^b f(z(t))\cdot \dot{z}(t)\,\mathrm{d}t</math> | ||
| + | ===Példa=== | ||
| + | '''1.''' Legyen ''G'' a komplex egységkör pozitívan irányítva. | ||
| + | :<math>\int\limits_{|z|=1}\frac{1}{z}\mathrm{d}z=\int\limits_{0}^{2\pi} \frac{1}{e^{\mathrm{i}t}}\cdot \mathrm{i}e^{\mathrm{i}t}\,\mathrm{d}t=\int\limits_{0}^{2\pi} \mathrm{i}\,\mathrm{d}t=2\pi\mathrm{i}</math> | ||
| + | Ahol a valós Newton--Leibniz-formulát alkalmaztuk a komponensfüggvényekre. | ||
| + | |||
| + | '''2.''' Legyen ''G'' a z(t)=(1+2i)t, ahol t∈[0,1]. | ||
| + | :<math>\int\limits_{G}\overline{z}\mathrm{d}z=\int\limits_{0}^{1} (1-2\mathrm{i})t\cdot (1+2\mathrm{i})\,\mathrm{d}t=\int\limits_{0}^{1}5t\,\mathrm{d}t=\frac{5}{2}</math> | ||
| + | |||
| + | '''3.''' Legyen ''G'' a komplex egységkör felső fele, pozitívan irányítva. | ||
| + | :<math>\int\limits_{|z|=1,\mathrm{Im}(z)\geq 0}\overline{z}^2\mathrm{d}z=\int\limits_{0}^{\pi}e^{-2\mathrm{i}t}\cdot \mathrm{i}e^{\mathrm{i}t}\,\mathrm{d}t=\int\limits_{0}^{\pi}e^{-\mathrm{i}t}\,\mathrm{d}t=1-(-1)=2</math> | ||
| + | |||
| + | ===Komplex Newton--Leibniz-formula=== | ||
| + | Ha az f komplex függvény, olyan, hogy van olyan komplex differenciálható F, melyre F'=f, akkor azt mondjuk, hogy a F az f primitív függvénye. | ||
| + | |||
| + | '''Komplex Newton--Leibniz-formula.''' Ha a nyílt halmazon értelmezett f komplex függvénynek primitív függvénye az F és f folytonos, akkor minden az f értelmezési tartományában haladó ''G'':[a,b]<math>\to</math>'''C''' görbére: | ||
| + | :<math>\int\limits_{G}f(z)\,\mathrm{d}z=F(b)-F(a)</math> | ||
| + | |||
| + | Például: | ||
| + | |||
| + | '''4.''' Legyen <math>f(z)=\frac{1}{z^2}</math>. Mi az egységkörre az integrálja? | ||
| + | :<math>F(z)=-\frac{1}{z}</math> | ||
| + | primitívfüggvénye f-nek, ezért | ||
| + | :<math>\int\limits_{|z|=1}\frac{1}{z^2}\,\mathrm{d}z=0</math> | ||
| + | hiszen zárt a görbe, azaz a pr. fv. a kezdő és végpontban ugyanannyi. | ||
| + | |||
| + | |||
| + | |||
| + | ==Cirkulációmentesség== | ||
| + | '''Tétel.''' Ha a ''D'' tartományon értelmezett ''f'' függvénynek van primitív függvénye, akkor a körintegrál minden a ''D''-ben haladó folytonosan differenciálható (ill. ilyenek véges összekapcsolásain) zárt görbén eltűnik: | ||
| + | :<math>\oint f=0\,</math> | ||
| + | |||
| + | További információhoz akkor jutunk, ha a többváltozós analízis cirkuálciómentességi feltételeit vizsgáljuk. Ehhez a vissza kell vezetni a komplex integrált a vonalintegrálra. | ||
| + | |||
| + | Legyen ''f''(''z'') = ''f''(''x'',''y'') = ''u''(''x'',''y'') + i''v''(''x'',''y''). Ekkor ''f'' felfogható '''R'''<sup>2</sup> <math>\supset\!\to</math> '''R'''<sup>2</sup> függvényként, melynek vonalintegrálja a | ||
| + | :<math>G:z(t)\equiv\mathbf{r}(t)=(x(t),y(t))\,</math> | ||
| + | vonal mentén: | ||
| + | :<math>\int\limits_{G}f(z)\mathrm{d}z = \int\limits_{G} u\mathrm{d}x-v\mathrm{d }y + i\int\limits_{G} u\mathrm{d}y+v\mathrm{d }x</math> | ||
| + | amiben az | ||
| + | :<math>\mathbf{v}=\begin{pmatrix}u\\-v\end{pmatrix}</math> és <math>\mathbf{w}=\begin{pmatrix}v\\u\end{pmatrix}</math> | ||
| + | vektorterek integráljai szerepelnek. | ||
| + | |||
| + | Vagy kétdimenziós felületi integrálként: | ||
| + | |||
| + | :<math>\mathbf{v}'=\begin{pmatrix}-v\\-u\end{pmatrix}</math> és <math>\mathbf{w}'=\begin{pmatrix}u\\-v\end{pmatrix}</math> | ||
| + | |||
| + | Ugyanis a komplex vonalintegrált síkbeli felületi integrállá lehet alakítani: | ||
| + | :<math>\int \mathbf{v}\mathrm{d}\mathbf{A}=\int \mathbf{v}\times\mathrm{d}\mathbf{r}=\int v_1 \mathrm{d}y-v_2\mathrm{d}x</math> | ||
| + | |||
| + | |||
| + | ===Gauss-tétel=== | ||
| + | Lássuk először Gauss-tételle, hogyan következtethetünk a körintegrál eltűnésére. | ||
| + | |||
| + | '''Gauss-tétel''' ('''R'''<sup>3</sup>-ra) Legyen '''v''' nyílt halmazon értelmezett C<sup>1</sup>-függvény, ''V'' egyszeresen összefüggő, mérhető térrész és legyen ennek ∂''V'' határa kifelé irányított felület. Ha ''V'' a határával együtt Dom('''v''')-ben van, akkor | ||
| + | :<math>\oint\limits_{\partial V} \mathbf{v}\;\mathrm{d}\mathbf{A}=\int\limits_{V} \mathrm{div}\,\mathbf{v}\;\mathrm{d}V</math> | ||
| + | |||
| + | Az itt szereplő fogalmak közül néhányról beszélnünk kell. | ||
| + | |||
| + | '''Felület.''' Legyenek a φ<sup>i</sup>:D<sub>i</sub> <math>\to</math> '''R'''<sup>3</sup> függvények folytonosan differenciálhatóak és injektívek int(''D''<sub>i</sub>)-n, melyek mérhető tarományok '''R'''<sup>2</sup>-ben. Ha a képeik egymásba nem nyúlók, azaz int(φ<sub>i</sub>(''D''<sub>i</sub>)) ∩ int(φ<sub>j</sub>(''D''<sub>j</sub>)) üres, ha ''i'' ≠ ''j'', és a képek uniója összefüggő halmaz, akkor U Ran(φ<sup>i</sup>)-t előállítottuk paraméteres felületként. | ||
| + | |||
| + | Példaként említhetjük a kúp paraméterezését: | ||
| + | |||
| + | :<math>\mathbf{r}_1(\varphi, h)=\left\{\begin{matrix} h\sin\vartheta\cos \varphi\\ h\sin\vartheta\sin\varphi\\ h\end{matrix}\right.</math>, ha φ ∈ [0,2π] és ''h'' ∈ [0,''H''] | ||
| + | :<math>\mathbf{r}_2(\varphi, h)=\left\{\begin{matrix}r\cos\varphi\\r\sin\varphi \\ H\end{matrix}\right.</math>, ha φ ∈ [0,2π] és ''r'' ∈ [0,''R''] | ||
| + | ahol H a kúp magassága, R az alapkörsugara, θ a félkúpszöge (z a tengelye, O a csúcsa). Tehát itt a paramétertartományok [0,2π] × [0,''H''] és [0,2π] × [0,''R'']. | ||
| + | |||
| + | '''C<sup>1</sup>-ség'''. Ez azért kell, mert a térfogati integrált a ''D'' paramétertartományon a | ||
| + | :<math>\int\limits_{V} \mathrm{div}\,\mathbf{v}\;\mathrm{d}V=\int\limits_{\mathbf{r}^{-1}(V)}\mathrm{div}\,\mathbf{v}(\mathbf{r}(u,v,w))|\mathrm{J}^{\mathbf{r}}(u,v,w)|\;\mathrm{d}u\mathrm{d}v\mathrm{d}w</math> | ||
| + | képlettel számoljuk és ahhoz, hogy ez lézetten, ahhoz pl az kell, hogy ne csak az '''r''' = '''r'''(u,v,w) legyen folytonosan diff.-ható, de a divergencia is folytonos legyen. | ||
| + | |||
| + | '''Egyszeresen összefüggő tartomány.''' A G<sub>1</sub>: [a,b] <math>\to</math> '''R'''<sup>3</sup> és a G<sub>2</sub>: [a,b] <math>\to</math> '''R'''<sup>3</sup> görbék homotópak, ha létezik olyan ''F'': [0,1] × [a,b] <math>\to</math> '''R'''<sup>3</sup> folytonos függvény, hogy F(0,.) ≡ G<sub>1</sub> és F(1,.) ≡ G<sub>2</sub>.Ez gyakorlatilag azt jelenti, hogy a G<sub>1</sub> a G<sub>2</sub>-be folytonos transzformációval átvihető. Egyszeresen összefüggő egy tartomány, ha benne minden zárt görbe homotóp a konstans görbével. | ||
| + | |||
| + | Az egyszeres összefüggőség lényeges feltétel. Gondoljunk a '''v'''('''r''') = '''r'''/''r''<sup>3</sup> vektortérre. Ennek divergenciája 0, de az origó körüli zárt gömbfelület integrálja 4π. | ||
| + | |||
| + | '''Gauss-tétel''' ('''R'''<sup>2</sup>-re) Legyen D egyszeresen összefüggő, mérhető síktartomány és legyen G ≡ '''r'''(t) ennek határát paraméterező zárt görbe. Ha '''v''' folytonosan '''R'''-differenciálható a D lezártján, akkor | ||
| + | :<math>\oint\limits_{G} \mathbf{v}(\mathbf{r})\mathrm{d}\mathbf{A}=\int\limits_{D} \mathrm{div}\,(\mathbf{v})\mathrm{d}A</math> | ||
| + | |||
| + | Így tehát a komplex vonalintegrál kiszámításához csak a '''v''' ' és '''w''' ' felületi integrálját kell kiszámítanunk, amihez a Gauss-tétel miatt beli divergenciákat kell kiszámítanunk: | ||
| + | :<math>\mathrm{div}\mathbf{v}'=-\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}=0</math> | ||
| + | :<math>\mathrm{div}\mathbf{w}'=\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}=0</math> | ||
| + | Ami, a C-R-egyenletek miatt igaz. | ||
| + | |||
| + | Innen | ||
| + | :<math>\int\limits_{G}f(z)\mathrm{d}z=0</math> | ||
| + | |||
| + | ===Stokes-tétel=== | ||
| + | |||
| + | Nézzük meg Stokes-tétellel is a bizonyítást. | ||
| + | |||
| + | '''Stokes-tétel''' ('''R'''<sup>3</sup>-ra) Legyen a nyílt halmazon értelmezett '''v''' vektorfüggvény folytonosan differenciálható, a Dom('''v''')-beli F felület pereme legyen a szintén Dom('''v''')-beli G zárt, F-nek megfelelően irányított görbe. Ekkor | ||
| + | :<math>\oint\limits_{G} \mathbf{v}(\mathbf{r})\mathrm{d}\mathbf{r}=\int\limits_{F} \mathrm{rot}(\mathbf{v})\mathrm{d}\mathbf{F}</math> | ||
| + | |||
| + | A térbeli cirkulációmentességre vonatkozó nevezetes tétel ezzel a tétellel kapcsoltos. Ebben az esetben, bár az egyszeres összefüggőség nincs megkötve Dom('''v''')-re vonatkozólag, előjön a következményében: | ||
| + | |||
| + | '''Következmény.''' Ha az egyszeresen összefűggő ''D'' nyílt halmazon értelmezett '''v''' vektortér folytonosan differenciálható, akkor az alábbi három kijelentés ekvivaléens egymással: | ||
| + | # rot '''v''' eltűnik ''D''-n. | ||
| + | # minden ''D''-ben haladó zárt görbén a '''v''' körintegrálja nulla | ||
| + | # létezik '''v'''-nek ''D''-n potenciálja, azaz olyan Φ : ''D'' <math>\to</math> '''R'''<sup>3</sup> függvény, melyre grad Φ = '''v'''. | ||
| + | |||
| + | Itt az egyszeres összefüggőség azért kell, mert annyit biztosan tudunk, hogy ilyen esetben a zárt görbéhez található olyan felület, mely a tartományban halad és pereme a görbe. | ||
| + | |||
| + | '''Stokes-tétel''' ('''R'''<sup>2</sup>-re) Legyen a D síkbeli felület határán a G zárt görbe ( '''r'''(t) ). Ha '''v''' folytonosan '''R'''-differenciálható, akkor | ||
| + | :<math>\oint\limits_{G} \mathbf{v}(\mathbf{r})\mathrm{d}\mathbf{r}=\int\limits_{D} \mathrm{rot}(\mathbf{v})\mathrm{d}A</math> | ||
| + | |||
| + | Világos, hogy a D tartománynak egyszeresen összefüggőnek kell lennie ahhoz, hogy a G a határa legyen a D-nek. Ekkor csak a rotációt kell kiszámítanunk: | ||
| + | |||
| + | :<math>\mathrm{rot}\mathbf{v}=\frac{\partial u}{\partial y} - \left(-\frac{\partial v}{\partial x}\right)=0</math> | ||
| + | :<math>\mathrm{rot}\mathbf{w}=\frac{\partial v}{\partial y} - \frac{\partial u}{\partial x}=0</math> | ||
| + | |||
| + | Ami, a C-R-egyenletek miatt igaz. | ||
| + | |||
| + | ===Goursat-lemma, Cauchy-féle integráltétel=== | ||
| + | |||
| + | Goursat ennél is mélyebb eredményt talált: | ||
| + | |||
| + | |||
| + | '''Goursat-lemma'''. A T háromszöglapon reguláris ''f'' komplex függvény integrálja a háromszög határán nulla: | ||
| + | :<math>\oint\limits_{\partial T}f=0\,</math> | ||
| + | |||
| + | Innen már könnyen adódik a komplex analízis főtétele, melyet először Cauchy modott ki ugyan csak folytonosan diffható komplex függvényre, de Goursat ezt megfejelte a gyengített feltételével: | ||
| + | |||
| + | '''Főtétel.''' Ha a ''D'' tartományon egyszeresen összefüggő tartoányon reguláris az ''f'' komplex függvény, akkor a tartományban minden zárt G görbén a függvény integrálja nulla: | ||
| + | :<math>\oint\limits_{G} f=0\,</math> | ||
| + | |||
| + | |||
==Komplex sorozatok== | ==Komplex sorozatok== | ||
A lap 2013. október 23., 07:44-kori változata
Tartalomjegyzék |
C-differenciálhatóság
A komplex differenciálhatóság az előző észrevételekkel szoros kapcsolatban lesz. Egyfelől
mutaja, hogy ha a Jacobi-mártix hasonlóképpen viselkedik a komplex számok mátrixreprezentációjában, mint az egyváltozós valós derivált. Másrészt a
mutatja, hogy nem minden valósan deriválható függvény lesz komplex deriválható. Nézzük akkor az egyváltozós valós mintájára a definíciót majd lássuk a komplex differenciálhatóság jellemzését.
Definíció - Komplex differenciálhatóság, komplex derivált - Legyen f a z0 egy környezetében értelmezett függvény. Azt mondjuk, hogy f C-deriválható z0-ban és deriváltja a w szám, ha
Jelölése: f'(z0).
Azt, hogy az f a z0-ban komplex deriválható még úgy is jelöljük, hogy
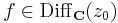 .
.
Pontbeli deriváltra példa a következő.
Példa. Milyen n egész számokra deriválható a 0-ban az alábbi függvény?
Mo. Ha n>0, akkor a különbségi hányados:
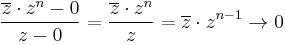 ha z
ha z  0.
0.
Ha n = 0, akkor
aminek nincs határértéke a 0-ban (az egységkörön mozog a végpont).
Ha n < 0, akkor
ami a 0-ban a komplex végtelenbe tart, mert a hossza a végtelenbe tart.
Tehát n > 0-ra a függvény komplex deriválható a 0-ban, más n < 1-re nem deriválható.
Tétel. - A komplex differenciálhatóság jellemzése - Legyen f a z0 = x0 + iy0 egy környezetében értelmezett függvény. Ekkor az alábbiak ekvivalensek:
- 1)
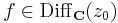
- 2)
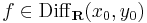 és
és ![[\mathrm{d}f(x_0,y_0)]\in\mathbf{C}](/upload/math/b/9/7/b975f630a8a50e0bde8a08b28b2c681d.png) .
.
Bizonyítás. Legyen f a z0 = x0 + iy0 egy környezetében értelmezett függvény és w' komplex szám. Tekintsük a következő határértéket:
Ha ez létezik, akkor ekvivalens a következővel:
Azaz
Itt (z-z0)/|z-z0| a komplex egységkörön "futó" függvény, ezért a fenti ekvivalnes a következővel:
Ami viszont ugyanakkor igaz mint:
Ha a következtetésben felfelé vizsgálódunk, tehát feltesszük a komplex deriválhatóságot ahol w a komplex derivált, akkor azt kapjuk, hogy a w mátrixreprezentációjával való mátrixszorzás alkalmas lineáris leképezés a valós derivált számára, azaz létezik [df(z0)]=[w].
Másfelől, ha f valósan deriválható és a deriváltja a w komplex számot reprezentálja, akkor komplexen is deriválható.
Cauchy--Riemann-egyenletek A fenti tételben a [df(z)] ∈ C feltétel (természetesen a totális deriválhatóság esetén) ekvivalens az alábbiakkal. Ha f = u + iv és z = x +iy, akkor
Komplex deriváltfüggvény Ahol egy f komplex függvény komplex deriválható, ott a deriváltja:
Definíció - Regularitás - Az f komplex függvény reguláris a z pontban, ha f a z egy egész környezetén értelmezett, és a teljes környezetben komplex deriválható.
Feladat. Legyen f(x+iy)=|x|+i|y|. Hol komplex deriválható és hol reguláris f?
Feladat. Legyen f(x + iy) = x2 + iy3. Hol komplex deriválható és hol reguláris f?
Harmonikus társ keresése
Azt mondjuk, hogy a kétszer differenciálható u=u(x,y) valós függvény harmonikus, ha
itt Δ a Laplace-operátor (nem a Laplace-transzformátor!, hanem a vektoranalízisbeli vektormezőre Hesse-mátrix nyoma).
A C--R-egyenletek mutatják, hogy ha f=u+iv reguláris, akkor u és v harmonikus függvények. Ugyanis:
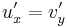 és
és
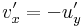
De u és v Hesse-mátrixa is szimmetrikus, ezért:
azaz
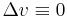 és fordítva.
és fordítva.
Általában az a feladat, hogy ha adott u, akkor keressük az ő harmonikus társát, v-t, mellyel u+iv reguláris. Ha tehát adott u, akkor van F és G, hogy
Ami az egzakt differenciálegynlet megoldásánál tanult parciális differenciálegyenlet megoldását igényli v-re, mint potenciálfüggvényre (ekkor f-et komplex pontenciálnak nevezzük, mármint a (v'x(x,y),vy'(x,y)) síkbeli vektormező komplex pontenciáljának; a v valódi pontenciálja lenne. Ennek szükséges utánanézni máshol is!)
1.. Keressünk harmonikus párt az
függvényhez!
Mo. Van neki, ha Δ=0. Ezt ellenőrizni kell, majd az előző módszerrel megkeresi v-t, amivel u+iv reguláris.
Komplex integrál
Görbék a komplex síkon
Ha G:[a,b] C, t
C, t z(t) folytonosan differenciálható, akkor G-t görbének nevezzük. (Esetleg a folytonos, véges sok helyen nem folytonosan differenciálható előbbi G-ket is görbéknek nevezzük.) A G görbe egyszerű, ha nem metszi át saját magát, azaz minden t1, t2-re, ha z(t1) = z(t2), akkor t1 = t2. G zárt, ha z(a) = z(b). A görbe t-beli irányvektorán a
z(t) folytonosan differenciálható, akkor G-t görbének nevezzük. (Esetleg a folytonos, véges sok helyen nem folytonosan differenciálható előbbi G-ket is görbéknek nevezzük.) A G görbe egyszerű, ha nem metszi át saját magát, azaz minden t1, t2-re, ha z(t1) = z(t2), akkor t1 = t2. G zárt, ha z(a) = z(b). A görbe t-beli irányvektorán a
komplex számot értjük.
Példák
1. Legyen t∈[a,b]-re z(t) = x(t) + iy(t) olyan, hogy x(t) = x0 + w1t és y(t) = y0 + w2t, azaz z(t) = z0 + wt. Ekkor z(t) egy egyenes szakasz.
És ekkor:
2. Az origó középpontú R sugarú kör:
- z(t) = Reit t∈[0,2π]
És ekkor
hiszen
Komplex vonalmenti integrál
Definíció. Ha G:[a,b] C görbe és f olyan komplex függvény, melyre Ran(G)⊆Dom(f), és f folytonos, akkor belátható, hogy létezik a
C görbe és f olyan komplex függvény, melyre Ran(G)⊆Dom(f), és f folytonos, akkor belátható, hogy létezik a
határérték, mely egy speciális Riemann-közelítőösszeg határértéke. Itt a görbén kijelöltük a véges sok zi pontot, melyek a szigorúan monoton (ti)-khez tartoznak a zi = z(ti) definícióval. Ezen [z(ti),z(ti + 1)] görbeszakaszokon belül felvettük tetszőlegesen a ζi közbülső pontokat, és a Δzi=[z(ti),z(ti + 1)] szakaszokkal elkészítettük az f(ζi)Δzi komplex szorzatokat. A határérték ezek görbére vett összegének határértéke. Ez a határérték az f függvény G-re vett komplex integrálja.
Visszavezetés valós vonalintegrálra. Az integrál kifejezhető vonalintegrállal. Ha ugyanis f= u + iv, akkor az f=(u,v) vektormezőnek olyan differenciálforma szerinti integrálja a komplex pályamenti integrál, mely az f=(u,v) vektor és a dz=(dx,dy) infinitezimális elmozdulásvektor komplex szorzásaként jön létre:
Ebben a felírásban az (u,-v) és (v,u) olyan segédvektormezők, melyek vonalintegráljai adják meg a komplex integrál valós és képzetes részét. Tehát az integrált a
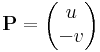 és
és 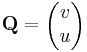
segédvektormezők síkbeli vonalintegráljai, vagy a
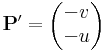 és
és 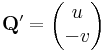
segédvektormezők síkbeli felületi integráljai szolgáltatják.
Itt érdemes feleleveníteni, hogy az S = (s1, s2) síkvektormező felületi integrálja nem más, mint a ( − s2, s1) vektormező vonalintegrálja (a megfelelő irányítással).
megfelelő módon irányítva az F felületet, ill ennek "F" görbe mivoltát.
(Azaz a s_2dx - s_1 dy differenciálforma integrálja. Differenciálforma -- nemes egyszerűséggel -- egy olyan kifejezése, ahol dx, dy, dz-k és egy vektormező komponensei vannak összeszorozva-összeadva.)
Kiszámítási formula. Belátható, hogy a fenti integrál a következőkkel egyenlő:
Példa
1. Legyen G a komplex egységkör pozitívan irányítva.
Ahol a valós Newton--Leibniz-formulát alkalmaztuk a komponensfüggvényekre.
2. Legyen G a z(t)=(1+2i)t, ahol t∈[0,1].
3. Legyen G a komplex egységkör felső fele, pozitívan irányítva.
Komplex Newton--Leibniz-formula
Ha az f komplex függvény, olyan, hogy van olyan komplex differenciálható F, melyre F'=f, akkor azt mondjuk, hogy a F az f primitív függvénye.
Komplex Newton--Leibniz-formula. Ha a nyílt halmazon értelmezett f komplex függvénynek primitív függvénye az F és f folytonos, akkor minden az f értelmezési tartományában haladó G:[a,b] C görbére:
C görbére:
Például:
4. Legyen 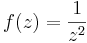 . Mi az egységkörre az integrálja?
. Mi az egységkörre az integrálja?
primitívfüggvénye f-nek, ezért
hiszen zárt a görbe, azaz a pr. fv. a kezdő és végpontban ugyanannyi.
Cirkulációmentesség
Tétel. Ha a D tartományon értelmezett f függvénynek van primitív függvénye, akkor a körintegrál minden a D-ben haladó folytonosan differenciálható (ill. ilyenek véges összekapcsolásain) zárt görbén eltűnik:
További információhoz akkor jutunk, ha a többváltozós analízis cirkuálciómentességi feltételeit vizsgáljuk. Ehhez a vissza kell vezetni a komplex integrált a vonalintegrálra.
Legyen f(z) = f(x,y) = u(x,y) + iv(x,y). Ekkor f felfogható R2  R2 függvényként, melynek vonalintegrálja a
R2 függvényként, melynek vonalintegrálja a
vonal mentén:
amiben az
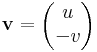 és
és 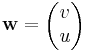
vektorterek integráljai szerepelnek.
Vagy kétdimenziós felületi integrálként:
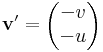 és
és 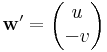
Ugyanis a komplex vonalintegrált síkbeli felületi integrállá lehet alakítani:
Gauss-tétel
Lássuk először Gauss-tételle, hogyan következtethetünk a körintegrál eltűnésére.
Gauss-tétel (R3-ra) Legyen v nyílt halmazon értelmezett C1-függvény, V egyszeresen összefüggő, mérhető térrész és legyen ennek ∂V határa kifelé irányított felület. Ha V a határával együtt Dom(v)-ben van, akkor
Az itt szereplő fogalmak közül néhányról beszélnünk kell.
Felület. Legyenek a φi:Di  R3 függvények folytonosan differenciálhatóak és injektívek int(Di)-n, melyek mérhető tarományok R2-ben. Ha a képeik egymásba nem nyúlók, azaz int(φi(Di)) ∩ int(φj(Dj)) üres, ha i ≠ j, és a képek uniója összefüggő halmaz, akkor U Ran(φi)-t előállítottuk paraméteres felületként.
R3 függvények folytonosan differenciálhatóak és injektívek int(Di)-n, melyek mérhető tarományok R2-ben. Ha a képeik egymásba nem nyúlók, azaz int(φi(Di)) ∩ int(φj(Dj)) üres, ha i ≠ j, és a képek uniója összefüggő halmaz, akkor U Ran(φi)-t előállítottuk paraméteres felületként.
Példaként említhetjük a kúp paraméterezését:
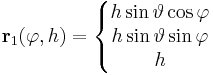 , ha φ ∈ [0,2π] és h ∈ [0,H]
, ha φ ∈ [0,2π] és h ∈ [0,H]
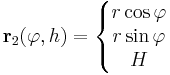 , ha φ ∈ [0,2π] és r ∈ [0,R]
, ha φ ∈ [0,2π] és r ∈ [0,R]
ahol H a kúp magassága, R az alapkörsugara, θ a félkúpszöge (z a tengelye, O a csúcsa). Tehát itt a paramétertartományok [0,2π] × [0,H] és [0,2π] × [0,R].
C1-ség. Ez azért kell, mert a térfogati integrált a D paramétertartományon a
képlettel számoljuk és ahhoz, hogy ez lézetten, ahhoz pl az kell, hogy ne csak az r = r(u,v,w) legyen folytonosan diff.-ható, de a divergencia is folytonos legyen.
Egyszeresen összefüggő tartomány. A G1: [a,b]  R3 és a G2: [a,b]
R3 és a G2: [a,b]  R3 görbék homotópak, ha létezik olyan F: [0,1] × [a,b]
R3 görbék homotópak, ha létezik olyan F: [0,1] × [a,b]  R3 folytonos függvény, hogy F(0,.) ≡ G1 és F(1,.) ≡ G2.Ez gyakorlatilag azt jelenti, hogy a G1 a G2-be folytonos transzformációval átvihető. Egyszeresen összefüggő egy tartomány, ha benne minden zárt görbe homotóp a konstans görbével.
R3 folytonos függvény, hogy F(0,.) ≡ G1 és F(1,.) ≡ G2.Ez gyakorlatilag azt jelenti, hogy a G1 a G2-be folytonos transzformációval átvihető. Egyszeresen összefüggő egy tartomány, ha benne minden zárt görbe homotóp a konstans görbével.
Az egyszeres összefüggőség lényeges feltétel. Gondoljunk a v(r) = r/r3 vektortérre. Ennek divergenciája 0, de az origó körüli zárt gömbfelület integrálja 4π.
Gauss-tétel (R2-re) Legyen D egyszeresen összefüggő, mérhető síktartomány és legyen G ≡ r(t) ennek határát paraméterező zárt görbe. Ha v folytonosan R-differenciálható a D lezártján, akkor
Így tehát a komplex vonalintegrál kiszámításához csak a v ' és w ' felületi integrálját kell kiszámítanunk, amihez a Gauss-tétel miatt beli divergenciákat kell kiszámítanunk:
Ami, a C-R-egyenletek miatt igaz.
Innen
Stokes-tétel
Nézzük meg Stokes-tétellel is a bizonyítást.
Stokes-tétel (R3-ra) Legyen a nyílt halmazon értelmezett v vektorfüggvény folytonosan differenciálható, a Dom(v)-beli F felület pereme legyen a szintén Dom(v)-beli G zárt, F-nek megfelelően irányított görbe. Ekkor
A térbeli cirkulációmentességre vonatkozó nevezetes tétel ezzel a tétellel kapcsoltos. Ebben az esetben, bár az egyszeres összefüggőség nincs megkötve Dom(v)-re vonatkozólag, előjön a következményében:
Következmény. Ha az egyszeresen összefűggő D nyílt halmazon értelmezett v vektortér folytonosan differenciálható, akkor az alábbi három kijelentés ekvivaléens egymással:
- rot v eltűnik D-n.
- minden D-ben haladó zárt görbén a v körintegrálja nulla
- létezik v-nek D-n potenciálja, azaz olyan Φ : D
 R3 függvény, melyre grad Φ = v.
R3 függvény, melyre grad Φ = v.
Itt az egyszeres összefüggőség azért kell, mert annyit biztosan tudunk, hogy ilyen esetben a zárt görbéhez található olyan felület, mely a tartományban halad és pereme a görbe.
Stokes-tétel (R2-re) Legyen a D síkbeli felület határán a G zárt görbe ( r(t) ). Ha v folytonosan R-differenciálható, akkor
Világos, hogy a D tartománynak egyszeresen összefüggőnek kell lennie ahhoz, hogy a G a határa legyen a D-nek. Ekkor csak a rotációt kell kiszámítanunk:
Ami, a C-R-egyenletek miatt igaz.
Goursat-lemma, Cauchy-féle integráltétel
Goursat ennél is mélyebb eredményt talált:
Goursat-lemma. A T háromszöglapon reguláris f komplex függvény integrálja a háromszög határán nulla:
Innen már könnyen adódik a komplex analízis főtétele, melyet először Cauchy modott ki ugyan csak folytonosan diffható komplex függvényre, de Goursat ezt megfejelte a gyengített feltételével:
Főtétel. Ha a D tartományon egyszeresen összefüggő tartoányon reguláris az f komplex függvény, akkor a tartományban minden zárt G görbén a függvény integrálja nulla:
Komplex sorozatok
Minthogy C ≡ R2 (mint normált vektortér), a komplex sorozatok azon tulajdonságai, melyek a vektortérműveletekkel és az | . | ≡ || . ||2 euklideszi normával kapcsolatosak mind R2-ből ismertnek tekinthetők. A sorozatok konvergenciáját ugyanúgy definiáljuk, mint R2-ben:
Ekkor a fenti z egyértelmű, és ez a sorozat határértéke (lim(zn))
A legfontosabb jellemzése tehát a konvergenciának az R2-ből kölcsönzött, a komponensekre vonatkozó kritérium:
Tétel – A C-beli (zn) = (an + ibn) sorozat konvergens akkor és csak akkor, ha
- (an) konvergens és
- (bn) konvergens.
Ekkor lim(zn) = lim(an) + i lim(bn)
lim(bn)
Fontos látni a kapcsolatot a sorozathatárék és a függvényhatárérték között. Egy (ζn) komplex sorozat nem más, mint egy
függvény. Ha Z-t komplex részhalmaznak gondoljuk (ahogy az is), akkor az egyetlen torlódási pontja a ∞. Ezért egy sorozatnak pontosan akkor létezik határértéke és ez a w szám, ha mint függvénynek létezik határértéke és az a w. Azaz:
Ebből következik, hogy a függvényhatárértékre vonatkozó minden műveleti szabály öröklődik a sorozathatárértékre.
Nullsorozatok
A 0 komplex számhoz tartó sorozatok nullsorozatok. Az abszolútérték és a szorzás jó tulajdonságai miatt öröklődnek a valós sorozatok alábbi tulajdonságai.
Állítás – Legyen (zn) komplex számsorozat.
- abszolútérték: zn
 0 akkor és csak akkor, ha |zn|
0 akkor és csak akkor, ha |zn|  0
0
- eltolás: zn
 z akkor és csak akkor, ha (zn – z)
z akkor és csak akkor, ha (zn – z)  0
0
- "K
 0": ha (wn) korlátos és zn
0": ha (wn) korlátos és zn  0, akkor (wn
0, akkor (wn  zn)
zn)  0
0
- majoráns: ha (δn)
 0 valós és |zn| < δn, akkor zn
0 valós és |zn| < δn, akkor zn  0
0
- hányadoskritérium: ha
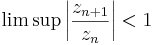 , akkor zn
, akkor zn  0
0
- gyökkritérium: ha
![\limsup\sqrt[n]{|z_n|}<1\,](/upload/math/c/1/a/c1a8b8217114281734effeccc096c4c5.png) , akkor zn
, akkor zn  0
0
Ezek közül C-ben a legjellegzetesebb a "K  0", hiszen ez azt állítja, hogy nem csak a λn.zn skalárral történő szorzás esetén igaz a "korlátos - nullához" tartó kritérium (mindkét változóban), hanem komplex szorzás is ilyen.
0", hiszen ez azt állítja, hogy nem csak a λn.zn skalárral történő szorzás esetén igaz a "korlátos - nullához" tartó kritérium (mindkét változóban), hanem komplex szorzás is ilyen.
1. Feladat
(Útmutatás: hivatkozzunk a "korlátos szor nullához tartó" kritériumra.)
2. Feladat.
ahol az n-edik gyök a valós számból vont valós gyök.
(Útmutatás: "i-telenítsük" a nevezőt.)
ugyanis
3. Feladat.
(Útmutatás: használjunk trigonometrikus alakot és hatványozzunk.)
Mert a szögfüggvények argumentumában lévő sorozat az 1-hez tart (pl L'Hospital-szabállyal majd átviteli elvvel ellenőrizhető), a első szorzó pedig az 1-ehez tart (rendőrelvvel). Az argumentumokban lévő értéket tertmészetesen radiánban kell venni: nem 1˚, hanem 1 rad.
Komplex sorok
Minden normált térben definiálhatók sorok és ezek konvergenciája, így C-ben is. Az (zn) sorozat
részletösszegeinek (sn) sorozatát a (zn) -ből képzett sornak nevezzük és ∑(zn)-nel jelöljük. Azt mondjuk, hogy a ∑(zn) sor konvergens és összege a w komplex szám, ha (zn) részletösszegeinek sorozata konvergens és határértéke w. Ekkor az összeget a
szimbólummal jelöljük.
Komponensek
Az egyik módja, hogy a komplex sorok konvergenciáját visszavezessük a valósokra, ha a komponenssorozatokat vesszük:
esetén az összegeket elképzelve, azokból az i kiemelhető, így
ahol az összeget és a szorzást tagonként végezzük. Ekkor egy sor ponrosan akkor konvergens, ha mindkét komponense konvergens.
Cauchy-kritérium és abszolút konvergencia
Világos, hogy egy sor, mint részletösszegsorozat pontosan akkor konvergens, ha Cauchy-sorozat. Ez a Cauchy-kritérium sorokra.
Létezik az abszolút konvergencia fogalmai is. Egy sor abszolút konvergens, ha a tagjai abszolútértékéből képezett sorozat konvergens. Igaz az, hogy egy normált tér akkor és csak akkor teljes, ha minden abszolút konvergens sor konvergens benne. (És C teljes, mert minden Cauchy-sorozat konvergál benne, ami pont annak a módja, hogy belássuk az előbbi kritériumot.) Persze az előfordul a teljes terekben is, hogy konvergens sorozatok nem lesznek abszolút konvergensek.
Kritériumok az abszolút konvergenciára
Az abszolút konvergencia fenti kritériumából egy sor komplex sorokra vonatkozó kritérium adódik a valósból.
Tétel – Legyen (zn) komplex számsorozat.
- Szükséges kritérium: Ha ∑(zn) konvergens, akkor (zn) nulsorozat.
- Geometriai sor: ha |z| < 1, akkor
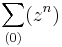 konvergens és az összege:
konvergens és az összege:
- Összehasonlító kritérium: ha az ∑(rn) valós sor konvergens és |zn| ≤ rn majdnem minden n-re, akkor ∑(zn) abszolút konvergens (majoráns-kritérium). Ha az ∑(rn) pozitív valós sor divergens és rn ≤ |zn| m.m., akkor ∑(zn) divergens (minoráns-kritérium).
- p-edik hatvány próba: ha p > 1 valós, akkor a
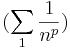 valós sor konvergens.
valós sor konvergens.
- Ha 0 ≤ p ≤ 1, akkor a
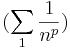 valós sor divergens.
valós sor divergens.
- Ha 0 ≤ p ≤ 1, akkor a
- Hányadoskritérium: ha
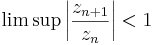 , akkor ∑(zn) abszolút konvergens. Ha a "liminf" > 1, akkor divergens
, akkor ∑(zn) abszolút konvergens. Ha a "liminf" > 1, akkor divergens
- Gyökkritérium: ha
![\limsup\sqrt[n]{|z_n|}<1\,](/upload/math/c/1/a/c1a8b8217114281734effeccc096c4c5.png) , akkor ∑(zn) abszolút konvergens. Ha a "limsup" > 1, akkor divergens.
, akkor ∑(zn) abszolút konvergens. Ha a "limsup" > 1, akkor divergens.
Megjegyezzük, hogy ha a gyökök és hányadosok sorozata konvergál, akkor ugyanahhoz a számhoz konvergálnak.
4.
Konvergens-e illetve abszolút konvergens-e?
5.
- Konvergens-e és mi a határértéke:
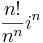
- Konvergens-e
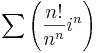
- Milyen z-re konvergens:
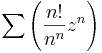
(Útmutatás: használjuk a hányadoskritériumot, vagy vizsgáljuk, hogy milyen rendben tartanak a végtelenhez az összetevősorozatok.)
azaz 0-hoz tart-
6.
- Konvergens-e és mi a határértéke:
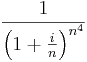
- Konvergens-e
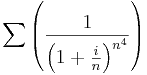
- Milyen z-re konvergens:
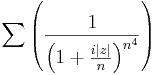
(Útmutatás: használjuk a gyökkritériumot.)
Így a reciproka a 0-hoz tart, azaz a limszup < 1.
Komplex hatványsorok
Definíció – Hatványsor – Legyen (an) komplex számsorozat és z0 ∈ C. Ekkor az ∑(an(idC-z0)n) függvénysort hatványsornak nevezzük és összegét, az
hozzárendelési utasítással értelmezett, a {z ∈ | ∑(an(z-z0)n) konvergál } halmazon értelmezett függvényt a hatványsor összegének nevezzük. Középpontja z0, együtthatósorozata (an).
A továbbiakban csak a ∑(anzn) alakú, azaz a 0 körüli hatványsorokkal foglalkozunk (ezzel nem csorbítjuk az általánosságot, mert eltolással megkaphatjuk a többit is).
Tétel – Cauchy–Hadamard-tétel – Ha (an) komplex számsorozat, ![c= \limsup\limits_{n}\sqrt[n]{|a_n|}](/upload/math/0/8/a/08a549d611fba6d99576372e981e8b49.png) és
és
akkor ∑(anzn) abszolút konvergens a BR(0) gömbön és divergens a B1/R(∞) gömbön.
A tétel minden részletre kiterjedő bizonyítását nem végezzük el, csak utalunk rá, hogy nyilvánvaló, hogy a Cauchy-féle gyökkritériumot kell benne használni. A tételbeli R sugarat a hatványsor konvergenciasugarának nevezzük. R-et másként is kiszámíthajuk. Ha azt tudjuk, a hányadoskritérium alapján, hogy
akkor létezik és ezzel egyenlő az n-edik gyökök sorozata is:
ahol az idézőjel azt jelzi, hogy a konvergenciasugár lehet végtelen vagy 0 is.
7. Feladat. Mi az alábbi hatványsorok konvergenciaköre és -sugara?
Analitikusnak nevezünk egy f komplex függvényt, a z0 pontban, ha van olyan δ sugarú környezet és ∑(an(z-z0)n) hatványsor, hogy minden z ∈ Bδ(z0)-ra f érelmezett, ∑(an(z-z0)n) konvergens és
Ezt úgy jelöljük, hogy f ∈ Cω(z0).
8. Feladat
- Van-e olyan
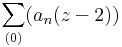 hatványsor, mely konvergál a 0-ban, de divergál a 3-ban. Konvergál 2-ben, de divergál az 2,000001-ben?
hatványsor, mely konvergál a 0-ban, de divergál a 3-ban. Konvergál 2-ben, de divergál az 2,000001-ben?
- Igazoljuk, hogy az alábbi függvény analitikus a nullában. Mi sorfejtés a konvergenciaköre?
Hatványsorok összegfüggvényének folytonossága és differenciálhatósága
Tétel – Ha (an) komplex számsorozat, akkor az ∑(anzn) hatványsor összegfüggvénye folytonos a konvergenciakör belsejében. Sőt, reguláris is ott.
Emlékeztetünk arra, hogy egy függvény reguláris egy pontban, ha a pont egy környezetében mindenütt értelmezett és komplex deriválható. A tétel szerint tehát analitikus függvény reguláris. A döbbenetes azonban, hogymint később kiderül: reguláris függvény analitikus: f ∈ Cω(z0) akkor és csak akkr, ha f ∈ Reg(z0).
Bizonyítás. Legyen z a konvergenciakör egy belső pontja és Δz olyan, hogy még z + Δz is a konvergenciakör belsejébe esik. Ekkor:
mert mindkét sor konvergens, ekkor algebrai azonosságokkal:
vagy ha tetszik nemnulla Δz-vel:
a jobb oldalon álló sor konvergenciáját a gyökkritériummal láthatjuk be:
ahol r olyan pozitív szám, hogy | z + Δz | < r < R (ez utóbbi a hatványsor konvergenciasugára). És
Így azt kaptuk, hogy minden olyan Δz-re, melyre | z + Δz | < r, teljesül és |Δz| <ε/(1+∑n|an|nrn)=:δ
Hosszadalmasabb számolásokkal, de lényegében ugyanígy kimutatható, hogy a hatványsor összegfüggvénye komplex differenciálható is a konvergenciakör belsejében és deriváltja a formális tagonkénti deriválásal kapott sor összegfüggvényével egyenlő, tehát:
Elemi függvények
Hatványfüggvények
A
típusú függvények komplex hatványfüggvények. n ∈ Z esetén, komplex deriváltjuk kiszámítható, n ≠ -1 esetben komplex primitív függvényük is van a következő értelemben:
Mivel
ezért n ≠ -1 esetén az az F(z) függvény, melyre 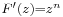 nem más, mint
nem más, mint
ahol C komplex konstans. n ≠ -1-re nincs primitív függvénye, mert a logaritmus nem egyértékű a komplex számok között.
Komplex vonalintegrál értelmezhető a G: [a,b]  C folytonos függvény, mint görbe esetén azzal a különlegességgel, hogy a szorzás a komplex szorzás:
C folytonos függvény, mint görbe esetén azzal a különlegességgel, hogy a szorzás a komplex szorzás:
Feltéve persze, hogy létezik és véges. Itt zi mindig a G görbe valamely pontját jelöli, amit az [a,b] egy felosztásának osztópontjainak G általi képeiből kapunk.
Ekkor fennáll a komplex Newton-Leibniz-formula. Ha a G görbe olyan nyílt halmazban halad, melyben az f-nek van primitív függvénye (egyértékű függvénye!) és f komplex integrálható, akkor z1 és z2 a végpontok esetén (a és b képe), a komplex integrál kiszámítható így:
Ha a görbe belép az f értelmezési tartományának olyan részére, melyben a függvénynek nincs egyértelmű primitív függvénye, akkor az integrál értéke függhet a G úttól.
1. Feladat. Legyen G a 3 középpontú, 1 sugarú kör felső félköre (pozitív irányítással). Számítsuk ki a
integrált.
2. Feladat. Legyen G az origó körüli 2 sugarú kör vonal. Mennyi az
- a)
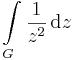 és a b)
és a b) 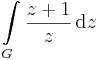
integrál.
A hatványfüggvények inverzei szintén nem egyértékű függvények.
Exponenciális függvény
Ebbőkkiderül az exponenciális függvény sok tulajdonsága. Például, ha z = x + iy, akkor
Ebből rögtön következik, hogy komplex exponenciális függvény periodikus, periódusa a p = 2πi:
3. Feladat. Oldjuk meg az
egyenletet!
Írjuk át 1+i-t exponenciális alakba:
így
4. Feladat. Oldjuk meg az
egyenletet!
Komplex logaritmus és a reciprok integrálja
Tekintsük a
hozzárendelést! Ha w-t exponenciális alakban írjuk, megfeleltethetjük egymásnak a z algebrai alakját w trigonometrikus alakjával:
azaz
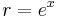 és
és 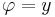
Ebből is látható, hogy a fordított leképezés végtelen sok értkű, hiszen ha y1 = 2π + y, akkor w(x+iy)= w(x+iy1 ). Ekkor a Riemann-felület egy végtelen sok Riemann-levélből áll.
Feladat. Számítsuk ki az alábbi integrálokat:
ahol G1 az egységkör a + irányban i-től -i-ig, G2 az egységkör a - irányban i-től -i-ig.
ahol Log a logaritmus főrésze, hisz a görbe a egy Rieman-levélen belül marad, míg
mivel itt áthalad a görbe a következő Riemann-levélre.
Más számítással:
Trigonometikus függvények
Világos, hogy valós φ-re:
A hiperbolikus függvényekhez hasonlóan a trigonometrikus függvények is előállnak de a komplex exponenciális segítségével:
5. Feladat. Igazoljuk, hogy fennáll
6. Feladat. Oldjuk meg az
egyenletet!
Hiperbolikus függvények
7. Feladat. Határozzuk meg az w = sh(iz) függvény valós és képzetes részét!
Mo.
8. Feladat. G az egységkör. Számítsuk ki
Mo.

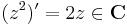
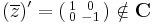
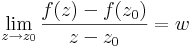
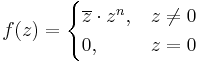
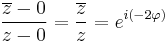
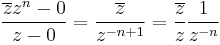
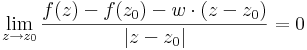
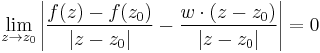
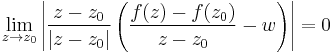
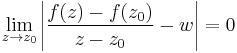
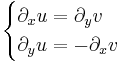
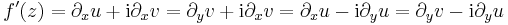
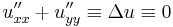
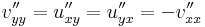
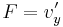
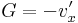
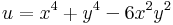
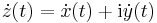
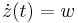
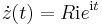
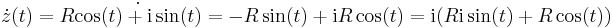
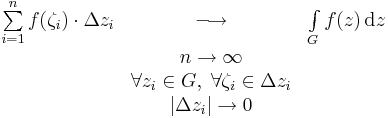
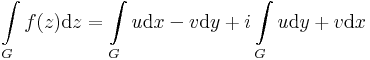
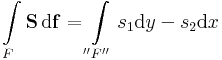
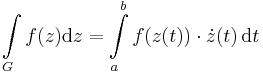
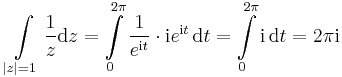
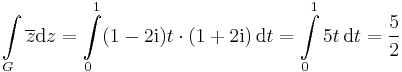
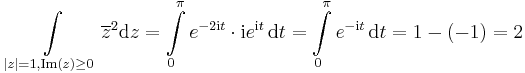
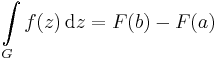
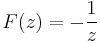
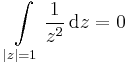
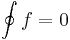
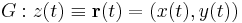
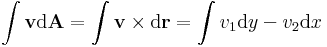
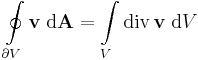
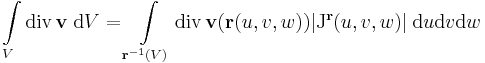
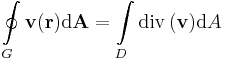
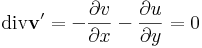
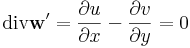
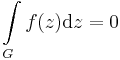
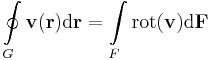
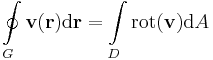
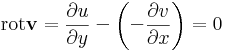
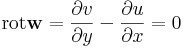
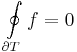
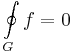
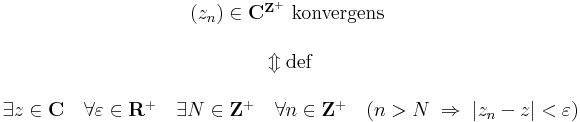
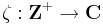
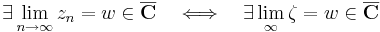
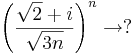
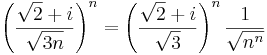
![\frac{\sqrt[n]{n^3+2n}}{i+1}\to ?](/upload/math/6/8/6/686b4f1dcc2e39ef2d30b890a1e8b99e.png)
![\frac{\sqrt[n]{n^3+2n}}{i+1}=\frac{(i-1)\sqrt[n]{n^3+2n}}{-1-1}=\frac{i\sqrt[n]{n^3+2n}-\sqrt[n]{n^3+2n}}{-2}\to \frac{1}{2}-\frac{1}{2}i](/upload/math/e/d/6/ed6bf5f9f7eb97cbe95dc9043cdf3ec6.png)
![1\leftarrow\sqrt[n]{n}^3=\sqrt[n]{n^3}\leq\sqrt[n]{n^3+2n}\leq\sqrt[n]{n^3+\frac{n^3}{2}}=\sqrt[n]{\frac{3}{2}n^3}=\sqrt[n]{\frac{3}{2}}\sqrt[n]{n}^3\to 1](/upload/math/f/3/d/f3d3d9b03a73cdf5affda73cd55f7a2a.png)
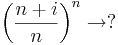
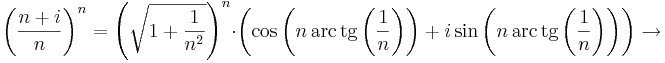
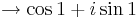
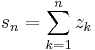
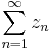
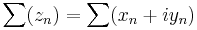
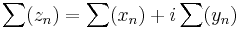
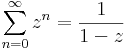
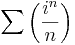
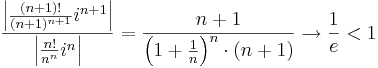
![\sqrt[n]{\left|1+\frac{i}{n}\right|^{n^4}}=\left|1+\frac{i}{n}\right|^{n^3}=\left(\sqrt{\left(1+\frac{1}{n^2}\right)^{n^2}}\right)^n\geq (1+\varepsilon)^n\to +\infty](/upload/math/3/f/0/3f0577419156648cce30f006027bd6ec.png)
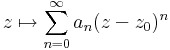
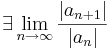
![\exists\lim\limits_{n\to \infty}\sqrt[n]{|a_n|}=\lim\limits_{n\to \infty}\frac{|a_{n+1}|}{|a_n|}=\,''\,\frac{1}{R}\,''](/upload/math/2/1/0/210b8f12a11f0846e6103b096dee2a3d.png)
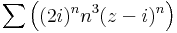
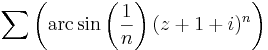
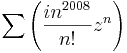
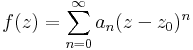
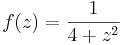
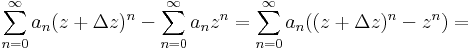
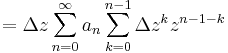
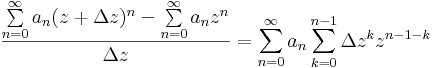
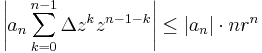
![\limsup\limits_{n\to \infty}\sqrt[n]{|a_n|\cdot n r^n}=\limsup\limits_{n\to \infty}\sqrt[n]{|a_n|}\cdot 1 \cdot r\leq\frac{1}{R}r<1\,](/upload/math/e/f/0/ef0679b874a4aae352293176852288ad.png)
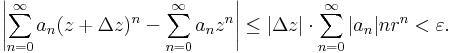
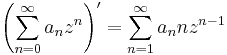
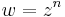
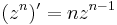
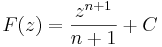
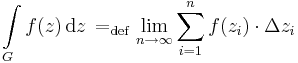
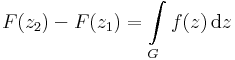
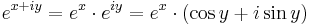
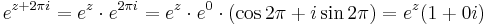
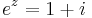
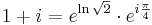
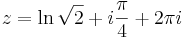
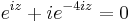
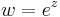
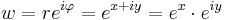
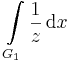
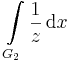
![\int\limits_{i,\,(G_1)}^{-i}\frac{1}{z}\mathrm{d}z=[\mathrm{Log}(z)]_{i}^-i=\mathrm{Log}(e^{i\frac{3}{2}\pi})-\mathrm{Log}(e^{\frac{1}{2}\pi})=i\pi\,](/upload/math/a/4/2/a42e365fce32cb21f8db2e0469a88fa0.png)
![\int\limits_{i,\,(G_2)}^{-i}\frac{1}{z}\mathrm{d}z=[\mathrm{Log}(z)]_{i}^-i=\mathrm{Log}(e^{-i\frac{1}{2}\pi})-\mathrm{Log}(e^{\frac{1}{2}\pi})=-i\pi\,](/upload/math/4/3/7/4374216d8c2e89e0aa46ef1f7f5d54b2.png)
![\int\limits_{i,\,(G_1)}^{-i}\frac{1}{z}\mathrm{d}z=\int\limits_{t=\frac{\pi}{2}}^{\frac{3\pi}{2}}\frac{1}{z(t)}\cdot\frac{\mathrm{d}z(t)}{\mathrm{d}t}\,\mathrm{d}t=\int\limits_{t=\frac{\pi}{2}}^{\frac{3\pi}{2}}e^{-it}ie^{it}\mathrm{d}t=[it]_{t=\frac{\pi}{2}}^{\frac{3\pi}{2}}](/upload/math/3/d/c/3dc40d6864883c4ca1fe553849dce88a.png)