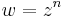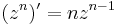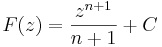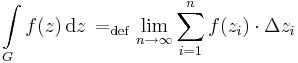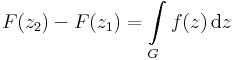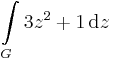Matematika A3a 2008/6. gyakorlat
Mozo (vitalap | szerkesztései) (→Hatványfüggvények) |
Mozo (vitalap | szerkesztései) (→Hatványfüggvények) |
||
| 18. sor: | 18. sor: | ||
Ekkor fennáll a komplex Newton-Leibniz-formula. Ha ''z''<sub>1</sub> és ''z''<sub>2</sub> a G két végpontja (''a'' és ''b'' képe), akkor a komplex integrál kiszámítható: | Ekkor fennáll a komplex Newton-Leibniz-formula. Ha ''z''<sub>1</sub> és ''z''<sub>2</sub> a G két végpontja (''a'' és ''b'' képe), akkor a komplex integrál kiszámítható: | ||
| − | <math>F(z_2)-F(z_1)=\int\limits_{G}f(z)\,\mathrm{d}z\,</math> | + | :<math>F(z_2)-F(z_1)=\int\limits_{G}f(z)\,\mathrm{d}z\,</math> |
| + | |||
| + | '''Feladat.''' Legyen G a 3 középpontú, 1 sugarú kör felső félköre (pozitív irányítással). Számítsuk ki a | ||
| + | :<math>\int\limits_{G}3z^2+1\,\mathrm{d}z\,</math> | ||
| + | integrált. | ||
[[Kategória:Matematika A3]] | [[Kategória:Matematika A3]] | ||
A lap 2008. október 30., 11:54-kori változata
Elemi függvények
Hatványfüggvények
A
típusú függvények komplex hatványfüggvények. n ∈ Z esetén, komplex deriváltjuk kiszámítható, n ≠ -1 esetben komplex primitív függvényük is van a következő értelemben:
Mivel
ezért n ≠ -1 esetén az az F(z) függvény, melyre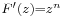 
nem más, mint
ahol C komplex konstans.
Komplex vonalintegrál értelmezhető a G: [a,b] 
C folytonos függvény, mint görbe esetén azzal a különlegességgel, hogy a szorzás a komplex szorzás:
Feltéve persze, hogy létezik és véges. Itt zi mindig a G görbe valamely pontját jelöli, amit az [a,b] egy felosztásának osztópontjainak G általi képeiből kapunk.
Ekkor fennáll a komplex Newton-Leibniz-formula. Ha z1 és z2 a G két végpontja (a és b képe), akkor a komplex integrál kiszámítható:
Feladat. Legyen G a 3 középpontú, 1 sugarú kör felső félköre (pozitív irányítással). Számítsuk ki a
integrált.
