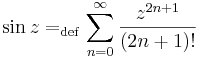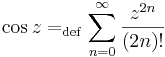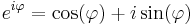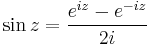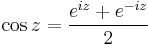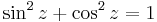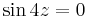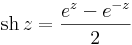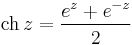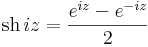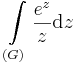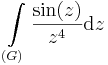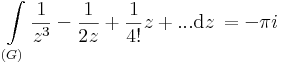Matematika A3a 2008/6. gyakorlat
Mozo (vitalap | szerkesztései) (→Elemi függvények) |
Mozo (vitalap | szerkesztései) (→Hiperbolikus függvények) |
||
| 111. sor: | 111. sor: | ||
'''8. Feladat.''' G az egységkör. Számítsuk ki | '''8. Feladat.''' G az egységkör. Számítsuk ki | ||
| − | :<math>\int\limits_{(G)}\frac{e^ | + | :<math>\int\limits_{(G)}\frac{e^z}{z}\mathrm{d}z\,</math> |
| + | :<math>\int\limits_{(G)}\frac{\sin(z)}{z^4}\mathrm{d}z\,</math> | ||
:<math>\int\limits_{(G)}\frac{1}{z}+1+\frac{1}{2}z+...\mathrm{d}z\,=2\pi i</math> | :<math>\int\limits_{(G)}\frac{1}{z}+1+\frac{1}{2}z+...\mathrm{d}z\,=2\pi i</math> | ||
| + | :<math>\int\limits_{(G)}\frac{1}{z^3}-\frac{1}{2z}+\frac{1}{4!}z+...\mathrm{d}z\,=-\pi i</math> | ||
| + | |||
[[Kategória:Matematika A3]] | [[Kategória:Matematika A3]] | ||
A lap 2008. október 30., 14:49-kori változata
Tartalomjegyzék |
Elemi függvények
Hatványfüggvények
A
típusú függvények komplex hatványfüggvények. n ∈ Z esetén, komplex deriváltjuk kiszámítható, n ≠ -1 esetben komplex primitív függvényük is van a következő értelemben:
Mivel
ezért n ≠ -1 esetén az az F(z) függvény, melyre 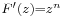 nem más, mint
nem más, mint
ahol C komplex konstans. n ≠ -1-re nincs primitív függvénye, mert a logaritmus nem egyértékű a komplex számok között.
Komplex vonalintegrál értelmezhető a G: [a,b]  C folytonos függvény, mint görbe esetén azzal a különlegességgel, hogy a szorzás a komplex szorzás:
C folytonos függvény, mint görbe esetén azzal a különlegességgel, hogy a szorzás a komplex szorzás:
Feltéve persze, hogy létezik és véges. Itt zi mindig a G görbe valamely pontját jelöli, amit az [a,b] egy felosztásának osztópontjainak G általi képeiből kapunk.
Ekkor fennáll a komplex Newton-Leibniz-formula. Ha a G görbe olyan nyílt halmazban halad, melyben az f-nek van primitív függvénye (egyértékű függvénye!) akkor z1 és z2 a végpontok esetén (a és b képe), a komplex integrál kiszámítható így:
Ha a görbe belép az f értelmezési tartományának olyan részére, melyben a függvénynek nincs egyértelmű primitív függvénye, akkor az integrál értéke függhet a G úttól.
1. Feladat. Legyen G a 3 középpontú, 1 sugarú kör felső félköre (pozitív irányítással). Számítsuk ki a
integrált.
2. Feladat. Legyen G az origó körüli 2 sugarú kör vonal. Mennyi az
integrál.
A hatványfüggvények inverzei szintén nem egyértékű függvények.
Exponenciális függvény
Ebbőkkiderül az exponenciális függvény sok tulajdonsága. Például, ha z = x + iy, akkor
Ebből rögtön következik, hogy komplex exponenciális függvény periodikus, periódusa a p = 2πi:
3. Feladat. Oldjuk meg az
egyenletet!
Írjuk át 1+i-t exponenciális alakba:
így
4. Feladat. Oldjuk meg az
egyenletet!
Komplex logaritmus és a reciprok integrálja
Tekintsük a
hozzárendelést! Ha w-t exponenciális alakban írjuk, megfeleltethetjük egymásnak a z algebrai alakját w trigonometrikus alakjával:
azaz
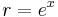 és
és 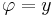
Ebből is látható, hogy a fordított leképezés végtelen sok értkű, hiszen ha y1 = 2π + y, akkor w(x+iy)= w(x+iy1 ). Ekkor a Riemann-felület egy végtelen sok Riemann-levélből áll.
Feladat. Számítsuk ki az alábbi integrálokat:
ahol G1 az egységkör a + irányban i-től -i-ig, G2 az egységkör a - irányban i-től -i-ig.
ahol Log a logaritmus főrésze, hisz a görbe a egy Rieman-levélen belül marad, míg
mivel itt áthalad a görbe a következő Riemann-levélre.
Más számítással:
Trigonometikus függvények
Világos, hogy valós φ-re:
A hiperbolikus függvényekhez hasonlóan a trigonometrikus függvények is előállnak de a komplex exponenciális segítségével:
5. Feladat. Igazoljuk, hogy fennáll
6. Feladat. Oldjuk meg az
egyenletet!
Hiperbolikus függvények
7. Feladat. Határozzuk meg az w = sh(iz) függvény valós és képzetes részét!
Mo.
8. Feladat. G az egységkör. Számítsuk ki
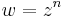
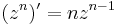
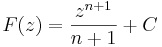
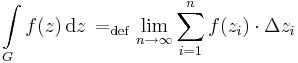
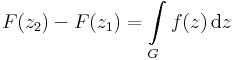
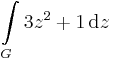
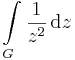
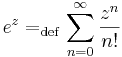
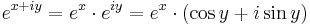
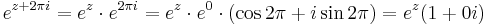
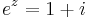
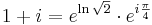
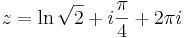
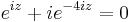
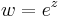
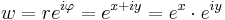
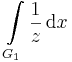
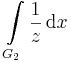
![\int\limits_{i,\,(G_1)}^{-i}\frac{1}{z}\mathrm{d}z=[\mathrm{Log}(z)]_{i}^-i=\mathrm{Log}(e^{i\frac{3}{2}\pi})-\mathrm{Log}(e^{\frac{1}{2}\pi})=i\pi\,](/upload/math/a/4/2/a42e365fce32cb21f8db2e0469a88fa0.png)
![\int\limits_{i,\,(G_2)}^{-i}\frac{1}{z}\mathrm{d}z=[\mathrm{Log}(z)]_{i}^-i=\mathrm{Log}(e^{-i\frac{1}{2}\pi})-\mathrm{Log}(e^{\frac{1}{2}\pi})=-i\pi\,](/upload/math/4/3/7/4374216d8c2e89e0aa46ef1f7f5d54b2.png)
![\int\limits_{i,\,(G_1)}^{-i}\frac{1}{z}\mathrm{d}z=\int\limits_{t=\frac{\pi}{2}}^{\frac{3\pi}{2}}\frac{1}{z(t)}\cdot\frac{\mathrm{d}z(t)}{\mathrm{d}t}\,\mathrm{d}t=\int\limits_{t=\frac{\pi}{2}}^{\frac{3\pi}{2}}e^{-it}ie^{it}\mathrm{d}t=[it]_{t=\frac{\pi}{2}}^{\frac{3\pi}{2}}](/upload/math/3/d/c/3dc40d6864883c4ca1fe553849dce88a.png)