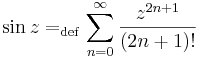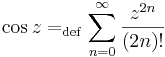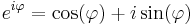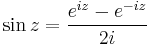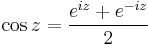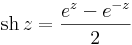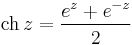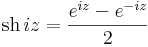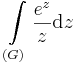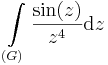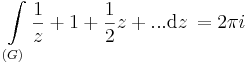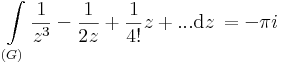Matematika A3a 2008/6. gyakorlat
Mozo (vitalap | szerkesztései) (→R-differenciálhatóság) |
Mozo (vitalap | szerkesztései) (→R-differenciálhatóság) |
||
| 9. sor: | 9. sor: | ||
szerint (itt ''u'' és ''v'' kétváltozós valós függvények, rendre az ''f'' valós és képzetes része). | szerint (itt ''u'' és ''v'' kétváltozós valós függvények, rendre az ''f'' valós és képzetes része). | ||
| − | ''f'' abban az értelemen '''R'''-differenciálható, ahogy az (''u'',''v''):'''R'''<sup>2</sup> <math>\ | + | ''f'' abban az értelemen '''R'''-differenciálható, ahogy az (''u'',''v''):'''R'''<sup>2</sup> <math>\supset\to</math> '''R'''<sup>2</sup> függvény differenciálható, azaz |
| − | '''Definíció''' -- Valós deriválhatóság -- Legyen ''g'':'''R'''<sup>2</sup> <math>\ | + | '''Definíció''' -- Valós deriválhatóság -- Legyen ''g'':'''R'''<sup>2</sup> <math>\supset\to</math> '''R'''<sup>2</sup>, ''x''<sub>0</sub>∈IntDom(g). Ekkor a ''g'' differenciálható az ''x''<sub>0</sub> pontban, ha létezik olyan ''A'': '''R'''<sup>2</sup> <math>\to</math> '''R'''<sup>2</sup> lineáris leképezés, melyre |
:<math>\exists \lim_{x\to x_0}\frac{f(x)-f(x_0)-A(x-x_0)}{||x-x_0||}=0</math> | :<math>\exists \lim_{x\to x_0}\frac{f(x)-f(x_0)-A(x-x_0)}{||x-x_0||}=0</math> | ||
ahol ||.|| tetszőleges norma (például az ||.||<sub>2</sub>=|.| komplex abszolútérték) '''R'''<sup>2</sup>-ben. | ahol ||.|| tetszőleges norma (például az ||.||<sub>2</sub>=|.| komplex abszolútérték) '''R'''<sup>2</sup>-ben. | ||
A lap 2012. november 2., 19:27-kori változata
Tartalomjegyzék |
Differenciálhatóság
R-differenciálhatóság
Legyen f : C ⊃ C komplex függvény. Ekkor f azonosítható az
C komplex függvény. Ekkor f azonosítható az
vektorértékű kétváltozós függvénnyel az
szerint (itt u és v kétváltozós valós függvények, rendre az f valós és képzetes része).
f abban az értelemen R-differenciálható, ahogy az (u,v):R2 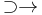 R2 függvény differenciálható, azaz
R2 függvény differenciálható, azaz
Definíció -- Valós deriválhatóság -- Legyen g:R2 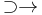 R2, x0∈IntDom(g). Ekkor a g differenciálható az x0 pontban, ha létezik olyan A: R2
R2, x0∈IntDom(g). Ekkor a g differenciálható az x0 pontban, ha létezik olyan A: R2  R2 lineáris leképezés, melyre
R2 lineáris leképezés, melyre
ahol ||.|| tetszőleges norma (például az ||.||2=|.| komplex abszolútérték) R2-ben.
Ekkor a fenti A lineáris leképezés egyértelmű és a jelölése: dg(x0).
Ekkor például a hozzáadás, mint affin függvény R-differenciálható, és R-differenciálja az identitás:
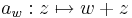 akkor
akkor 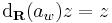
A komplex számmal szorzás R-differenciálját közvetlenül a definíciójából számíthatjuk ki:
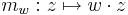 akkor
akkor 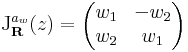
Rendkívül érdekes észrevétel tanúi lehetünk ekkor. z  w
w z R-deriváltja maga w komplex számnak megfelelő mátrix, azaz
z R-deriváltja maga w komplex számnak megfelelő mátrix, azaz
ha mátrixreprezentációt veszünk. Sőt, visszanézve ez az összeadásra is igaz:
Feladat. Számítsuk ki az f(z) = z2 R-differenciálját!
Legyen z = x + i y. Ekkor z2 = x2 - y2 +i(2xy)
Feladat. Számítsuk ki az 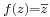 R-differenciálját!
R-differenciálját!
Ha z = x + i y, akkor 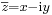 , így:
, így:
És ezzel már ki is mondhatjuk a Cauchy-Riemann-féle szükséges feltételt:
- Annak a szükséges feltétele, hogy az f:R2
 R2 R-differenciálható függvény differenciálja egy komplex szám mátrixreprezentációja legyen, az, hogy:
R2 R-differenciálható függvény differenciálja egy komplex szám mátrixreprezentációja legyen, az, hogy:
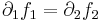 és
és 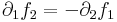
C-differenciálhatóság
A fenti példa motiválja a C-differenciálhatóság fogalmát. Legyen a szituáció az előbbi, azaz legyen f(z) totálisan differenciálható (mint kétváltozós függvény) a z0 pontban és a Jacobi-mátrixa ott legyen a w ∈ C szám mátrixreprezentációja. Ekkor
Itt w (z-z0) egyfelől a mátrixszorzás, másfelől a komplex szorzás. Ekkor:
(z-z0) egyfelől a mátrixszorzás, másfelől a komplex szorzás. Ekkor:
Ha h(z)=(z-z0)/|z-z0|, ami a komplex "egységgömbön" "futó" függvény, akkor a komplex szorzás tulajdonságai miatt:
Innen a következő gondolatunk támadhat. Teljesen az egyváltozós valós derivált tulajdonságait mutató deriváltfogalmat kapunk, ha bevezetődne a következő
Definíció - Komplex differenciálhatóság, komplex derivált - Legyen f a z0 egy környezetében értelmezett függvény. Azt mondjuk, hogy f C-deriválható z0-ban és deriváltja a w szám, ha
Most gondoljuk végig, hogy milyen kapcsolatban van az R'- és a C-deriválhatóság. Ha a fenti gondolamenetet felfelé nézzük, akkor a h(z) korlátossága miatt a "korlátos szor nullához" tartó függvényt kapunk, így a szorzat határértéke 0. Persze ehhez kellene a "korlátos szor nullához tartó" lemma komplex szorzásra.
Ha lefelé gondolkodunk, akkor indirekten kell eljárnunk. Tegyük fel, hogy a második tényező nem nulla határértékű. Amikor nem létezik, vagy nem az adott szám a határérték, akkor "cáfoló" sorozatot szoktunk megadni. Az átviteli elv miatt létezik olyan z(n) konvergens komplex sorozat, mely nem a 0-hoz tart. De a h(z(n)) ekkor az egységkörön van, így a szorzat biztosan "elerüli a nullát" (az abszolút értéke nem a 0-hoz tart). Következésképpen:
Tétel. A definícióbeli f pontosan akkor komplex differenciálható, ha differenciálható és a deriváltja komplex szám (mátrix reprezentációja). Továbbá f pontosan akkor komplex differenciálható, ha differenciálható és a parciális deriváltjai teljesítik a Cauchy-Riemann-egyenleteket.
Feladat. Komplex deriváljuk az f(z) = zn függvényt!
Feladat. Komplex deriválható-e: 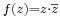 , vagy a
, vagy a 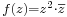 ?
?
Feladat. Igazoljuk, hogy ha f korlátos komplex függvény a D ⊆ C halmazon és limwg = 0, akkor limw fg = 0. (w ∈ int D).
Elemi függvények
Hatványfüggvények
A
típusú függvények komplex hatványfüggvények. n ∈ Z esetén, komplex deriváltjuk kiszámítható, n ≠ -1 esetben komplex primitív függvényük is van a következő értelemben:
Mivel
ezért n ≠ -1 esetén az az F(z) függvény, melyre 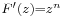 nem más, mint
nem más, mint
ahol C komplex konstans. n ≠ -1-re nincs primitív függvénye, mert a logaritmus nem egyértékű a komplex számok között.
Komplex vonalintegrál értelmezhető a G: [a,b]  C folytonos függvény, mint görbe esetén azzal a különlegességgel, hogy a szorzás a komplex szorzás:
C folytonos függvény, mint görbe esetén azzal a különlegességgel, hogy a szorzás a komplex szorzás:
Feltéve persze, hogy létezik és véges. Itt zi mindig a G görbe valamely pontját jelöli, amit az [a,b] egy felosztásának osztópontjainak G általi képeiből kapunk.
Ekkor fennáll a komplex Newton-Leibniz-formula. Ha a G görbe olyan nyílt halmazban halad, melyben az f-nek van primitív függvénye (egyértékű függvénye!) és f komplex integrálható, akkor z1 és z2 a végpontok esetén (a és b képe), a komplex integrál kiszámítható így:
Ha a görbe belép az f értelmezési tartományának olyan részére, melyben a függvénynek nincs egyértelmű primitív függvénye, akkor az integrál értéke függhet a G úttól.
1. Feladat. Legyen G a 3 középpontú, 1 sugarú kör felső félköre (pozitív irányítással). Számítsuk ki a
integrált.
2. Feladat. Legyen G az origó körüli 2 sugarú kör vonal. Mennyi az
- a)
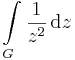 és a b)
és a b) 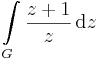
integrál.
A hatványfüggvények inverzei szintén nem egyértékű függvények.
Exponenciális függvény
Ebbőkkiderül az exponenciális függvény sok tulajdonsága. Például, ha z = x + iy, akkor
Ebből rögtön következik, hogy komplex exponenciális függvény periodikus, periódusa a p = 2πi:
3. Feladat. Oldjuk meg az
egyenletet!
Írjuk át 1+i-t exponenciális alakba:
így
4. Feladat. Oldjuk meg az
egyenletet!
Komplex logaritmus és a reciprok integrálja
Tekintsük a
hozzárendelést! Ha w-t exponenciális alakban írjuk, megfeleltethetjük egymásnak a z algebrai alakját w trigonometrikus alakjával:
azaz
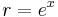 és
és 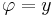
Ebből is látható, hogy a fordított leképezés végtelen sok értkű, hiszen ha y1 = 2π + y, akkor w(x+iy)= w(x+iy1 ). Ekkor a Riemann-felület egy végtelen sok Riemann-levélből áll.
Feladat. Számítsuk ki az alábbi integrálokat:
ahol G1 az egységkör a + irányban i-től -i-ig, G2 az egységkör a - irányban i-től -i-ig.
ahol Log a logaritmus főrésze, hisz a görbe a egy Rieman-levélen belül marad, míg
mivel itt áthalad a görbe a következő Riemann-levélre.
Más számítással:
Trigonometikus függvények
Világos, hogy valós φ-re:
A hiperbolikus függvényekhez hasonlóan a trigonometrikus függvények is előállnak de a komplex exponenciális segítségével:
5. Feladat. Igazoljuk, hogy fennáll
6. Feladat. Oldjuk meg az
egyenletet!
Hiperbolikus függvények
7. Feladat. Határozzuk meg az w = sh(iz) függvény valós és képzetes részét!
Mo.
8. Feladat. G az egységkör. Számítsuk ki
Mo.
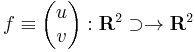
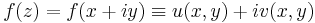
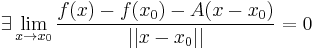
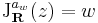
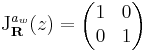
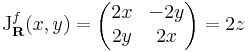
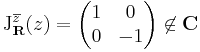
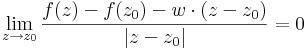
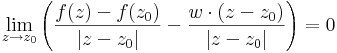
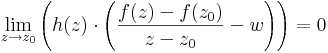
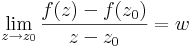
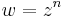
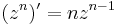
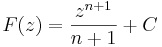
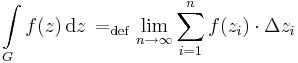
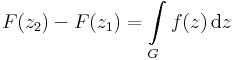
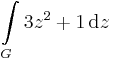
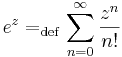
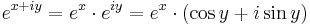
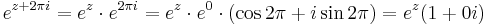
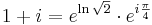
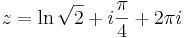
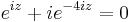
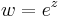
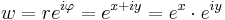
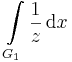
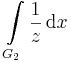
![\int\limits_{i,\,(G_1)}^{-i}\frac{1}{z}\mathrm{d}z=[\mathrm{Log}(z)]_{i}^-i=\mathrm{Log}(e^{i\frac{3}{2}\pi})-\mathrm{Log}(e^{\frac{1}{2}\pi})=i\pi\,](/upload/math/a/4/2/a42e365fce32cb21f8db2e0469a88fa0.png)
![\int\limits_{i,\,(G_2)}^{-i}\frac{1}{z}\mathrm{d}z=[\mathrm{Log}(z)]_{i}^-i=\mathrm{Log}(e^{-i\frac{1}{2}\pi})-\mathrm{Log}(e^{\frac{1}{2}\pi})=-i\pi\,](/upload/math/4/3/7/4374216d8c2e89e0aa46ef1f7f5d54b2.png)
![\int\limits_{i,\,(G_1)}^{-i}\frac{1}{z}\mathrm{d}z=\int\limits_{t=\frac{\pi}{2}}^{\frac{3\pi}{2}}\frac{1}{z(t)}\cdot\frac{\mathrm{d}z(t)}{\mathrm{d}t}\,\mathrm{d}t=\int\limits_{t=\frac{\pi}{2}}^{\frac{3\pi}{2}}e^{-it}ie^{it}\mathrm{d}t=[it]_{t=\frac{\pi}{2}}^{\frac{3\pi}{2}}](/upload/math/3/d/c/3dc40d6864883c4ca1fe553849dce88a.png)