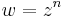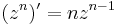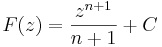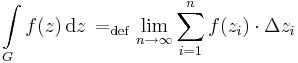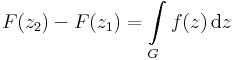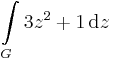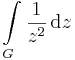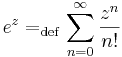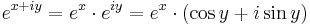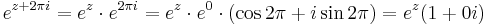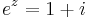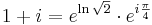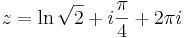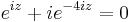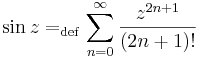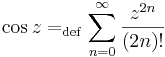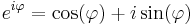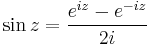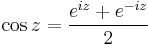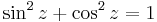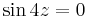Matematika A3a 2008/6. gyakorlat

_{<Matematika A3a 2008}

Elemi függvények

Hatványfüggvények

A

$w=z^n\,$

típusú függvények komplex hatványfüggvények. n ∈ Z esetén, komplex deriváltjuk kiszámítható, n ≠ -1 esetben komplex primitív függvényük is van a következő értelemben:

Mivel

$(z^n)'=nz^{n-1}\,$

ezért n ≠ -1 esetén az az F(z) függvény, melyre 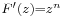$\scriptstyle{F'(z)=z^n}$ nem más, mint

$F(z)=\frac{z^{n+1}}{n+1}+C\,$

ahol C komplex konstans. n ≠ -1-re nincs primitív függvénye, mert a logaritmus nem egyértékű a komplex számok között.

Komplex vonalintegrál értelmezhető a G: [a,b] $\to$ C folytonos függvény, mint görbe esetén azzal a különlegességgel, hogy a szorzás a komplex szorzás:

$\int\limits_{G}f(z)\,\mathrm{d}z\,=_{\mathrm{def}}\lim\limits_{n \to \infty}\sum\limits_{i=1}^nf(z_i)\cdot\Delta z_i$

Feltéve persze, hogy létezik és véges. Itt z_i mindig a G görbe valamely pontját jelöli, amit az [a,b] egy felosztásának osztópontjainak G általi képeiből kapunk.

Ekkor fennáll a komplex Newton-Leibniz-formula. Ha a G görbe olyan nyílt halmazban halad, melyben az f-nek van primitív függvénye (egyértékű függvénye!) akkor z₁ és z₂ a végpontok esetén (a és b képe), a komplex integrál kiszámítható így:

$F(z_2)-F(z_1)=\int\limits_{G}f(z)\,\mathrm{d}z\,$

Ha a görbe belép az f értelmezési tartományának olyan részére, melyben a függvénynek nincs egyértelmű primitív függvénye, akkor az integrál értéke függhet a G úttól.

1. Feladat. Legyen G a 3 középpontú, 1 sugarú kör felső félköre (pozitív irányítással). Számítsuk ki a

$\int\limits_{G}3z^2+1\,\mathrm{d}z\,$

integrált.

2. Feladat. Legyen G az origó körüli 2 sugarú kör vonal. Mennyi az

$\int\limits_{G}\frac{1}{z^2}\,\mathrm{d}z\,$

integrál.

A hatványfüggvények inverzei szintén nem egyértékű függvények.

Exponenciális függvény

$e^z=_{\mathrm{def}}\sum\limits_{n=0}^{\infty}\frac{z^n}{n!}\,$

Ebbőkkiderül az exponenciális függvény sok tulajdonsága. Például, ha z = x + iy, akkor

$e^{x+iy}=e^x\cdot e^{iy}=e^x\cdot (\cos y + i\sin y)\,$

Ebből rögtön következik, hogy komplex exponenciális függvény periodikus, periódusa a p = 2πi:

$e^{z+2\pi i}=e^z\cdot e^{2\pi i}=e^z\cdot e^0\cdot (\cos 2\pi + i\sin 2\pi)=e^z(1+0i)\,$

3. Feladat. Oldjuk meg az

$e^z=1+i\;$

egyenletet!

Írjuk át 1+i-t exponenciális alakba:

$1+i=e^{\ln \sqrt{2}}\cdot e^{i\frac{\pi}{4}}\,$

így

$z=\ln\sqrt{2} +i\frac{\pi}{4}+2\pi i\,$

4. Feladat. Oldjuk meg az

$e^{iz}+ie^{-4iz}=0\,$

egyenletet!

Trigonometikus függvények

$\sin z=_{\mathrm{def}}\sum\limits_{n=0}^{\infty}\frac{z^{2n+1}}{(2n+1)!}\,$

$\cos z=_{\mathrm{def}}\sum\limits_{n=0}^{\infty}\frac{z^{2n}}{(2n)!}\,$

Világos, hogy valós φ-re:

$e^{i\varphi}=\cos(\varphi)+i\sin(\varphi)\,$

A hiperbolikus függvényekhez hasonlóan a trigonometrikus függvények is előállnak de a komplex exponenciális segítségével:

$\sin z=\frac{e^{iz}-e^{-iz}}{2i}$

$\cos z=\frac{e^{iz}+e^{-iz}}{2}$

4. Feladat. Igazoljuk, hogy fennáll

$\sin^2 z+ \cos^2z = 1\,$

5. Feladat. Oldjuk meg az

$\sin 4z=0\,$

egyenletet!