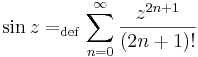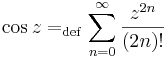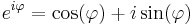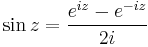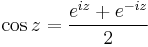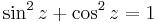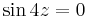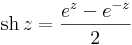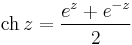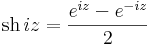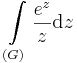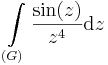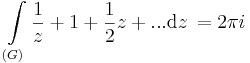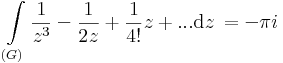Matematika A3a 2008/6. gyakorlat
Tartalomjegyzék |
Differenciálhatóság
R-differenciálhatóság
Legyen f : C ⊃ C komplex függvény. Ekkor f azonosítható az
C komplex függvény. Ekkor f azonosítható az
vektorértékű kétváltozós függvénnyel az
szerint (itt u és v kétváltozós valós függvények, rendre az f valós és képzetes része).
f abban az értelemen R-differenciálható, ahogy az (u,v):R2  R2 függvény differenciálható, azaz
R2 függvény differenciálható, azaz
Definíció -- Valós deriválhatóság -- Legyen g:R2  R2, x0∈IntDom(g). Ekkor a g differenciálható az x0 pontban, ha létezik olyan A: R2
R2, x0∈IntDom(g). Ekkor a g differenciálható az x0 pontban, ha létezik olyan A: R2  R2 lineáris leképezés, melyre
R2 lineáris leképezés, melyre
ahol ||.|| tetszőleges norma (például az ||.||2=|.| komplex abszolútérték) R2-ben.
Ekkor a fenti A lineáris leképezés egyértelmű és a jelölése: dg(x0). Azt, hogy a g valósan differenciálható (totálisan differenciálható) az x0-ban, még úgy is jelöljük, hogy
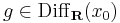 .
.
A df(x0,y0) leképezés sztenderd bázisban felírt koordinátamátrixát nevezzük Jacobi-mátrixnak, mely a következő. Ha f komponensfüggvényei: (x,y)  f(x,y) = (u(x,y),v(x,y)), akkor
f(x,y) = (u(x,y),v(x,y)), akkor
És persze, ha f differenciálható (értsd: totálisan differenciálhat, vagy valósan differenciálható), akkor parciálisan is deriválható, azaz a komponensfüggvényeinek az adott pontban léteznek a parciális deriváltjai, tehát felírható a Jacobi-mátrix.
Példák
1. Legyen w ∈ C tetszőlegesen rögzített és legyen
Ekkor a komponensfüggvények (f valós és képzetes része):
És a derivált:
Vegyük észre, hogy az imént kijött derivált éppen a w komplex szám mártixreprezentációja, hiszen általában egy z = a +' 'bi komplex szám mátrixreprezentációja:
a valós rész a főátlóban, a képzetes rész a -, + -szal a mellékátlóban van. Tehát:
2.
f(z) = z2
Legyen z = x + i y. Ekkor z2 = x2 - y2 +i(2xy)
azaz amit kaptunk, pont a 2z szám mátrixreprezentációja:
3. Számítsuk ki az 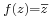 R-differenciálját!
R-differenciálját!
Ha z = x + i y, akkor 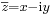 , így:
, így:
azaz nem mátrixreprezentáció alakú a Jacobi-mátrix. Ám, azt jegyezzük meg, hogy az iménti leképezés lineáris (ez az x tengelyre vonatkozó tükrözés), tehát folytonos, sőt totálisan (végtelenszer) differenciálható és a valós deriváltja pont saját maga:
csak nem komplex számot reprezentál a Jacobi-mátrix.
C-differenciálhatóság
A komplex differenciálhatóság az előző észrevételekkel szoros kapcsolatban lesz. Egyfelől
mutaja, hogy ha a Jacobi-mártix hasonlóképpen viselkedik a komplex számok mátrixreprezentációjában, mint az egyváltozós valós derivált. Másrészt a
mutatja, hogy nem minden valósan deriválható függvény lesz komplex deriválható. Nézzük akkor az egyváltozós valós mintájára a definíciót majd lássuk a komplex differenciálhatóság jellemzését.
Definíció - Komplex differenciálhatóság, komplex derivált - Legyen f a z0 egy környezetében értelmezett függvény. Azt mondjuk, hogy f C-deriválható z0-ban és deriváltja a w szám, ha
Jelölése: f'(z0).
Azt, hogy az f a z0-ban komplex deriválható még úgy is jelöljük, hogy
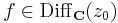 .
.
Pontbeli deriváltra példa a következő.
Példa. Milyen n egész számokra deriválható a 0-ban az alábbi függvény?
Mo. Ha n>0, akkor a különbségi hányados:
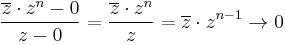 ha z
ha z  0.
0.
Ha n = 0, akkor
aminek nincs határértéke a 0-ban (az egységkörön mozog a végpont).
Ha n < 0, akkor
ami a 0-ban a komplex végtelenbe tart, mert a hossza a végtelenbe tart.
Tehát n > 0-ra a függvény komplex deriválható a 0-ban, más n < 1-re nem deriválható.
Tétel. - A komplex differenciálhatóság jellemzése - Legyen f a z0 = x0 + iy0 egy környezetében értelmezett függvény. Ekkor az alábbiak ekvivalensek:
- 1)
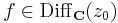
- 2)
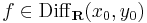 és
és ![[\mathrm{d}f(x_0,y_0)]\in\mathbf{C}](/upload/math/b/9/7/b975f630a8a50e0bde8a08b28b2c681d.png) .
.
Bizonyítás. Legyen f a z0 = x0 + iy0 egy környezetében értelmezett függvény és w' komplex szám. Tekintsük a következő határértéket:
Itt (z-z0)/|z-z0| a komplex egységkörön "futó" függvény, ezért a fenti ekvivalnes a következővel:
Ami viszont ugyanakkor igaz mint:
Ha a következtetésben felfelé vizsgálódunk, tehát feltesszük a komplex deriválhatóságot ahol w a komplex derivált, akkor azt kapjuk, hogy a w mátrixreprezentációjával való mátrixszorzás alkalmas lineáris leképezés a valós derivált számára, azaz létezik [df(z0)]=[w].
Másfelől, ha f valósan deriválható és a deriváltja a w komplex számot reprezentálja, akkor komplexen is deriválható.
Cauchy--Riemann-egyenletek A fenti tételben a [df(z)] ∈ C feltétel (természetesen a totális deriválhatóság esetén) ekvivalens az alábbiakkal. Ha f = u + iv és z = x +iy, akkor
Feladat. Komplex deriváljuk az f(z) = zn függvényt!
Feladat. Komplex deriválható-e: 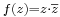 , vagy a
, vagy a 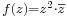 ?
?
Feladat. Igazoljuk, hogy ha f korlátos komplex függvény a D ⊆ C halmazon és limwg = 0, akkor limw fg = 0. (w ∈ int D).
Elemi függvények
Hatványfüggvények
A
típusú függvények komplex hatványfüggvények. n ∈ Z esetén, komplex deriváltjuk kiszámítható, n ≠ -1 esetben komplex primitív függvényük is van a következő értelemben:
Mivel
ezért n ≠ -1 esetén az az F(z) függvény, melyre 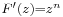 nem más, mint
nem más, mint
ahol C komplex konstans. n ≠ -1-re nincs primitív függvénye, mert a logaritmus nem egyértékű a komplex számok között.
Komplex vonalintegrál értelmezhető a G: [a,b]  C folytonos függvény, mint görbe esetén azzal a különlegességgel, hogy a szorzás a komplex szorzás:
C folytonos függvény, mint görbe esetén azzal a különlegességgel, hogy a szorzás a komplex szorzás:
Feltéve persze, hogy létezik és véges. Itt zi mindig a G görbe valamely pontját jelöli, amit az [a,b] egy felosztásának osztópontjainak G általi képeiből kapunk.
Ekkor fennáll a komplex Newton-Leibniz-formula. Ha a G görbe olyan nyílt halmazban halad, melyben az f-nek van primitív függvénye (egyértékű függvénye!) és f komplex integrálható, akkor z1 és z2 a végpontok esetén (a és b képe), a komplex integrál kiszámítható így:
Ha a görbe belép az f értelmezési tartományának olyan részére, melyben a függvénynek nincs egyértelmű primitív függvénye, akkor az integrál értéke függhet a G úttól.
1. Feladat. Legyen G a 3 középpontú, 1 sugarú kör felső félköre (pozitív irányítással). Számítsuk ki a
integrált.
2. Feladat. Legyen G az origó körüli 2 sugarú kör vonal. Mennyi az
- a)
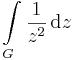 és a b)
és a b) 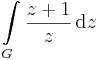
integrál.
A hatványfüggvények inverzei szintén nem egyértékű függvények.
Exponenciális függvény
Ebbőkkiderül az exponenciális függvény sok tulajdonsága. Például, ha z = x + iy, akkor
Ebből rögtön következik, hogy komplex exponenciális függvény periodikus, periódusa a p = 2πi:
3. Feladat. Oldjuk meg az
egyenletet!
Írjuk át 1+i-t exponenciális alakba:
így
4. Feladat. Oldjuk meg az
egyenletet!
Komplex logaritmus és a reciprok integrálja
Tekintsük a
hozzárendelést! Ha w-t exponenciális alakban írjuk, megfeleltethetjük egymásnak a z algebrai alakját w trigonometrikus alakjával:
azaz
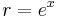 és
és 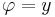
Ebből is látható, hogy a fordított leképezés végtelen sok értkű, hiszen ha y1 = 2π + y, akkor w(x+iy)= w(x+iy1 ). Ekkor a Riemann-felület egy végtelen sok Riemann-levélből áll.
Feladat. Számítsuk ki az alábbi integrálokat:
ahol G1 az egységkör a + irányban i-től -i-ig, G2 az egységkör a - irányban i-től -i-ig.
ahol Log a logaritmus főrésze, hisz a görbe a egy Rieman-levélen belül marad, míg
mivel itt áthalad a görbe a következő Riemann-levélre.
Más számítással:
Trigonometikus függvények
Világos, hogy valós φ-re:
A hiperbolikus függvényekhez hasonlóan a trigonometrikus függvények is előállnak de a komplex exponenciális segítségével:
5. Feladat. Igazoljuk, hogy fennáll
6. Feladat. Oldjuk meg az
egyenletet!
Hiperbolikus függvények
7. Feladat. Határozzuk meg az w = sh(iz) függvény valós és képzetes részét!
Mo.
8. Feladat. G az egységkör. Számítsuk ki
Mo.
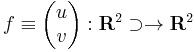
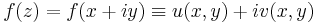
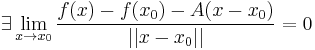
![\mathrm{J}^g(x_0,y_0)=[\mathrm{d}f(x_0,y_0)]=\begin{bmatrix}\partial_x u & \partial_y u \\\partial_x v & \partial_y v\end{bmatrix}(x_0,y_0)](/upload/math/3/4/2/342d296549ff91cf2601b4a8bde7f91b.png)

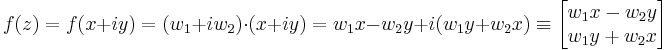
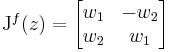
![[z]=\begin{bmatrix}
a & -b\\
b & a
\end{bmatrix}](/upload/math/2/7/7/277eedec9c464ad366d421eb71fcb5e5.png)
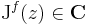
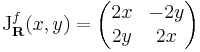
![\mathrm{J}^{f}(z)=[2z]\in\mathbf{C}](/upload/math/1/d/b/1db02ba7c867fd0c1ef9572f4417d48e.png)
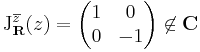
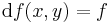

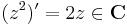
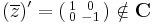
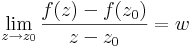
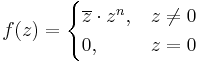
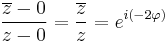
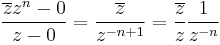
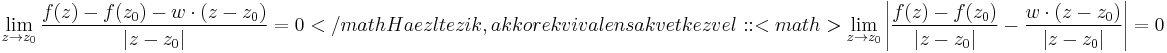
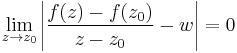
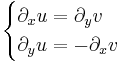
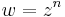
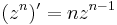
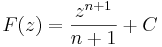
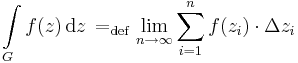
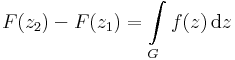
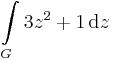
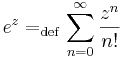
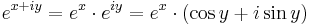
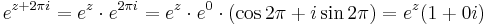
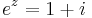
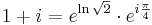
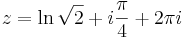
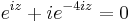
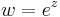
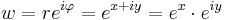
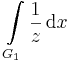
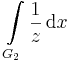
![\int\limits_{i,\,(G_1)}^{-i}\frac{1}{z}\mathrm{d}z=[\mathrm{Log}(z)]_{i}^-i=\mathrm{Log}(e^{i\frac{3}{2}\pi})-\mathrm{Log}(e^{\frac{1}{2}\pi})=i\pi\,](/upload/math/a/4/2/a42e365fce32cb21f8db2e0469a88fa0.png)
![\int\limits_{i,\,(G_2)}^{-i}\frac{1}{z}\mathrm{d}z=[\mathrm{Log}(z)]_{i}^-i=\mathrm{Log}(e^{-i\frac{1}{2}\pi})-\mathrm{Log}(e^{\frac{1}{2}\pi})=-i\pi\,](/upload/math/4/3/7/4374216d8c2e89e0aa46ef1f7f5d54b2.png)
![\int\limits_{i,\,(G_1)}^{-i}\frac{1}{z}\mathrm{d}z=\int\limits_{t=\frac{\pi}{2}}^{\frac{3\pi}{2}}\frac{1}{z(t)}\cdot\frac{\mathrm{d}z(t)}{\mathrm{d}t}\,\mathrm{d}t=\int\limits_{t=\frac{\pi}{2}}^{\frac{3\pi}{2}}e^{-it}ie^{it}\mathrm{d}t=[it]_{t=\frac{\pi}{2}}^{\frac{3\pi}{2}}](/upload/math/3/d/c/3dc40d6864883c4ca1fe553849dce88a.png)