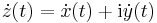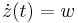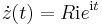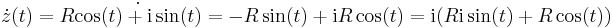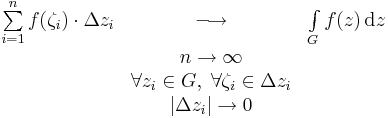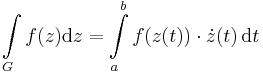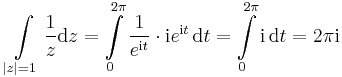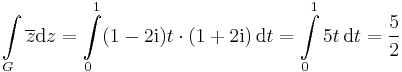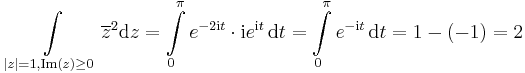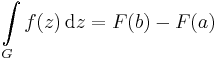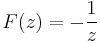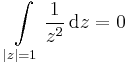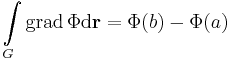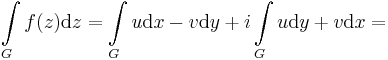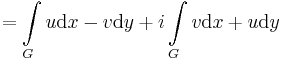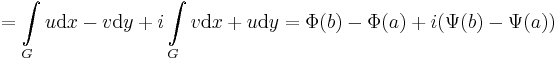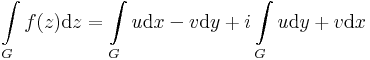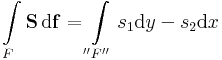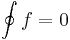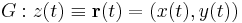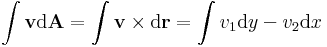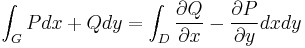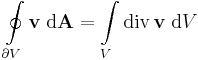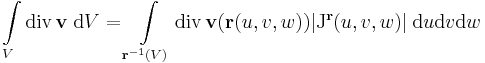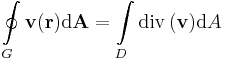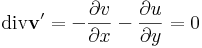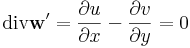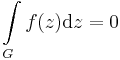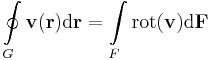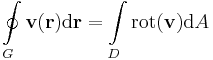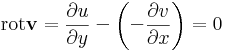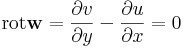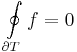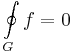Matematika A3a 2008/7. gyakorlat

A lap 2013. október 23., 07:46-kori változata (lapforrás) Mozo (vitalap | szerkesztései) ← Régebbi szerkesztés		A lap 2013. október 31., 12:22-kori változata (lapforrás) Mozo (vitalap | szerkesztései) Újabb szerkesztés →
1. sor:		1. sor:
	''<sub><[[Matematika A3a 2008]]</sub>''		''<sub><[[Matematika A3a 2008]]</sub>''
−	==Komplex sorozatok==	+	==Komplex integrál==
−	Minthogy '''C''' &equiv; '''R'''<sup>2</sup> (mint normált vektortér), a komplex sorozatok azon tulajdonságai, melyek a vektortérműveletekkel és az | . | &equiv; || . ||<sub>2</sub> euklideszi normával kapcsolatosak mind '''R'''<sup>2</sup>-ből ismertnek tekinthetők. A sorozatok konvergenciáját ugyanúgy definiáljuk, mint  '''R'''<sup>2</sup>-ben:	+
−	:<math>	+
−	\begin{matrix}	+
−	(z_n)\in\mathbf{C}^{\mathbf{Z}^+}\mbox{ konvergens }\\	+
−	\\	+
−	\Updownarrow\mathrm{def}\\	+
−	\\	+
−	\exists z\in \mathbf{C}\quad \forall \varepsilon\in\mathbf{R}^+\quad \exists N\in \mathbf{Z}^+\quad \forall n\in\mathbf{Z}^+ \quad(n> N\;\Rightarrow\;|z_n-z|<\varepsilon)	+
−	\end{matrix}</math>	+
−	Ekkor a fenti ''z'' egyértelmű, és ez a sorozat határértéke (lim(''z''<sub>n</sub>))	+
−	A legfontosabb jellemzése tehát a konvergenciának az '''R'''<sup>2</sup>-ből kölcsönzött, a komponensekre vonatkozó kritérium:	+	===Görbék a komplex síkon===
−	'''Tétel''' – A '''C'''-beli (''z''<sub>n</sub>) = (''a''<sub>n</sub> + i''b''<sub>n</sub>) sorozat konvergens akkor és csak akkor, ha	+	Ha ''G'':[''a'',''b'']<math>\to</math>'''C''', ''t''<math>\mapsto</math>''z''(''t'') folytonosan differenciálható, akkor ''G''-t görbének nevezzük. (Esetleg a folytonos, véges sok helyen nem folytonosan differenciálható előbbi ''G''-ket is görbéknek nevezzük.) A ''G'' görbe ''egyszerű'', ha nem metszi át saját magát, azaz minden <math>t_1</math>, <math>t_2</math>-re, ha <math>z(t_1)=z(t_2)</math>, akkor <math>t_1=t_2</math>. ''G'' zárt, ha <math>z(a)=z(b)</math>. A görbe ''t''-beli irányvektorán a
−	:(''a''<sub>n</sub>) konvergens és	+	:<math>\dot{z}(t)=\dot{x}(t)+\mathrm{i}\dot{y}(t)</math>
−	:(''b''<sub>n</sub>) konvergens.	+	komplex számot értjük.
−	Ekkor lim(''z''<sub>n</sub>) = lim(''a''<sub>n</sub>) + i<math>\cdot</math>lim(''b''<sub>n</sub>)	+	====Példák====
		+	'''1.''' Legyen ''t''&isin;[a,b]-re ''z''(''t'') = ''x''(''t'') + i''y''(''t'') olyan, hogy <math>x(t)=x_0+w_1t</math> és <math>y(t)=y_0+w_2t</math>, azaz <math>z(t)=z_0+w t</math>. Ekkor ''z''(''t'') egy egyenes szakasz.
−	Fontos látni a kapcsolatot a sorozathatárék és a függvényhatárérték között. Egy (''&zeta;''<sub>n</sub>) komplex sorozat nem más, mint egy	+	És ekkor:
−	:<math>\zeta: \mathbf{Z}^+\to \mathbf{C}</math>	+	:<math>\dot{z}(t)=w</math>
−	függvény. Ha '''Z'''<sup></sup>-t komplex részhalmaznak gondoljuk (ahogy az is), akkor az egyetlen torlódási pontja a &infin;. Ezért egy sorozatnak pontosan akkor létezik határértéke és ez a w szám, ha mint függvénynek létezik határértéke és az a w. Azaz:	+	'''2.''' Az origó középpontú R sugarú kör:
−	:<math>\exists\lim\limits_{n\to \infty}z_n=w\in\overline{\mathbf{C}}\quad\Longleftrightarrow\quad\exists\lim\limits_{\infty}\zeta=w\in\overline{\mathbf{C}}</math>	+	:<math>z(t)=Re^{\mathrm{i}t}</math> ''t''&isin;[0,2&pi;]
−	Ebből következik, hogy a függvényhatárértékre vonatkozó minden műveleti szabály öröklődik a sorozathatárértékre.	+	És ekkor
−	===Nullsorozatok===	+	:<math>\dot{z}(t)=R\mathrm{i}e^{\mathrm{i}t}</math>
		+	hiszen
		+	:<math>\dot{z}(t)=R\dot{\cos(t)+\mathrm{i}\sin(t)}=-R\sin(t)+\mathrm{i}R\cos(t)=\mathrm{i}(R\mathrm{i}\sin(t)+R\cos(t))</math>
		+	===Komplex vonalmenti integrál===
		+	'''Definíció.''' Ha ''G'':[a,b]<math>\to</math>'''C''' görbe és f olyan komplex függvény, melyre Ran(G)&sube;Dom(f), és f folytonos, akkor belátható, hogy létezik a
−	A 0 komplex számhoz tartó sorozatok nullsorozatok. Az abszolútérték és a szorzás jó tulajdonságai miatt öröklődnek a valós sorozatok alábbi tulajdonságai.	+	:<math>\begin{matrix}
		+	\sum\limits_{i=1}^nf(\zeta_i)\cdot \Delta z_i & \longrightarrow & \int\limits_{G}f(z)\,\mathrm{d}z\\
		+	& n\to \infty & \\
		+	& \forall z_i\in G, \;\forall \zeta_i\in \Delta z_i &\\
		+	& |\Delta z_i|\to 0 &
		+	\end{matrix}</math>
		+	határérték, mely egy speciális Riemann-közelítőösszeg határértéke. Itt a görbén kijelöltük a véges sok <math>z_i</math> pontot, melyek a szigorúan monoton (<math>t_i</math>)-khez tartoznak a <math>z_i=z(t_i)</math> definícióval. Ezen <math>[z(t_i),z(t_{i+1})]</math> görbeszakaszokon belül felvettük tetszőlegesen a &zeta;<sub>i</sub> közbülső pontokat, és a &Delta;z<sub>i</sub>=<math>[z(t_i),z(t_{i+1})]</math> szakaszokkal elkészítettük az f(&zeta;<sub>i</sub>)&Delta;z<sub>i</sub> komplex szorzatokat. A határérték ezek görbére vett összegének határértéke. Ez a határérték az f függvény ''G''-re vett komplex integrálja.
−	'''Állítás''' – Legyen (''z''<sub>n</sub>) komplex számsorozat.
−	# ''abszolútérték:'' ''z''<sub>n</sub> <math>\to</math> 0 akkor és csak akkor, ha |''z''<sub>n</sub>| <math>\to</math> 0
−	# ''eltolás:'' ''z''<sub>n</sub> <math>\to</math> ''z'' akkor és csak akkor, ha (''z''<sub>n</sub> – ''z'') <math>\to</math> 0
−	# ''"K <math> \cdot</math> 0":'' ha (''w''<sub>n</sub>) korlátos és ''z''<sub>n</sub> <math>\to</math> 0, akkor  (''w''<sub>n</sub> <math>\cdot</math> ''z''<sub>n</sub>) <math>\to</math> 0
−	# ''majoráns:'' ha (&delta;<sub>n</sub>) <math>\to</math> 0 valós és |''z''<sub>n</sub>| < &delta;<sub>n</sub>, akkor ''z''<sub>n</sub> <math>\to</math> 0
−	# ''hányadoskritérium:'' ha <math>\limsup\left|\frac{z_{n+1}}{z_n}\right|<1\,</math>, akkor  ''z''<sub>n</sub> <math>\to</math> 0
−	# ''gyökkritérium:'' ha <math>\limsup\sqrt[n]{|z_n|}<1\,</math>, akkor  ''z''<sub>n</sub> <math>\to</math> 0
		+	'''Kiszámítási formula.''' Belátható, hogy a fenti integrál a következőkkel egyenlő:
		+	:<math>
		+	\int\limits_{G}f(z)\mathrm{d}z=\int\limits_{a}^b f(z(t))\cdot \dot{z}(t)\,\mathrm{d}t</math>
−	Ezek közül '''C'''-ben a legjellegzetesebb a ''"K <math> \cdot</math> 0"'', hiszen ez azt állítja, hogy nem csak a &lambda;<sub>n</sub>.''z''<sub>n</sub> skalárral történő szorzás esetén igaz a "korlátos - nullához" tartó kritérium (mindkét változóban), hanem komplex szorzás is ilyen.	+	===Példa===
		+	'''1.''' Legyen ''G'' a komplex egységkör pozitívan irányítva.
		+	:<math>\int\limits_{|z|=1}\frac{1}{z}\mathrm{d}z=\int\limits_{0}^{2\pi} \frac{1}{e^{\mathrm{i}t}}\cdot \mathrm{i}e^{\mathrm{i}t}\,\mathrm{d}t=\int\limits_{0}^{2\pi} \mathrm{i}\,\mathrm{d}t=2\pi\mathrm{i}</math>
		+	Ahol a valós Newton--Leibniz-formulát alkalmaztuk a komponensfüggvényekre.
		+	'''2.''' Legyen ''G'' a z(t)=(1+2i)t, ahol t&isin;[0,1].
		+	:<math>\int\limits_{G}\overline{z}\mathrm{d}z=\int\limits_{0}^{1} (1-2\mathrm{i})t\cdot (1+2\mathrm{i})\,\mathrm{d}t=\int\limits_{0}^{1}5t\,\mathrm{d}t=\frac{5}{2}</math>
−	'''1. Feladat'''	+	'''3.''' Legyen ''G'' a komplex egységkör felső fele, pozitívan irányítva.
−	:<math>\left(\frac{\sqrt{2}+i}{\sqrt{3n}}\right)^n\to ?</math>	+	:<math>\int\limits_{|z|=1,\mathrm{Im}(z)\geq 0}\overline{z}^2\mathrm{d}z=\int\limits_{0}^{\pi}e^{-2\mathrm{i}t}\cdot \mathrm{i}e^{\mathrm{i}t}\,\mathrm{d}t=\int\limits_{0}^{\pi}e^{-\mathrm{i}t}\,\mathrm{d}t=1-(-1)=2</math>
−	''(Útmutatás: hivatkozzunk a "korlátos szor nullához tartó" kritériumra.)''	+	===Komplex Newton--Leibniz-formula===
−		+	Ha az f komplex függvény, olyan, hogy van olyan komplex differenciálható F, melyre F'=f, akkor azt mondjuk, hogy a F az f primitív függvénye.
−	:<math>\left(\frac{\sqrt{2}+i}{\sqrt{3n}}\right)^n=\left(\frac{\sqrt{2}+i}{\sqrt{3}}\right)^n\frac{1}{\sqrt{n^n}}</math>	+
−	'''2. Feladat.'''	+	'''Komplex Newton--Leibniz-formula.''' Ha a nyílt halmazon értelmezett f komplex függvénynek primitív függvénye az F és f folytonos, akkor minden az f értelmezési tartományában haladó ''G'':[a,b]<math>\to</math>'''C''' görbére:
−	:<math>\frac{\sqrt[n]{n^3+2n}}{i+1}\to ?</math>	+	:<math>\int\limits_{G}f(z)\,\mathrm{d}z=F(b)-F(a)</math>
−	ahol az ''n''-edik gyök a valós számból vont valós gyök.	+
−	''(Útmutatás: "i-telenítsük" a nevezőt.)''	+	Például:
−	:<math>\frac{\sqrt[n]{n^3+2n}}{i+1}=\frac{(i-1)\sqrt[n]{n^3+2n}}{-1-1}=\frac{i\sqrt[n]{n^3+2n}-\sqrt[n]{n^3+2n}}{-2}\to \frac{1}{2}-\frac{1}{2}i</math>	+	'''4.''' Legyen <math>f(z)=\frac{1}{z^2}</math>. Mi az egységkörre az integrálja?
−	ugyanis	+	:<math>F(z)=-\frac{1}{z}</math>
−	: <math>1\leftarrow\sqrt[n]{n}^3=\sqrt[n]{n^3}\leq\sqrt[n]{n^3+2n}\leq\sqrt[n]{n^3+\frac{n^3}{2}}=\sqrt[n]{\frac{3}{2}n^3}=\sqrt[n]{\frac{3}{2}}\sqrt[n]{n}^3\to 1</math>	+	primitívfüggvénye f-nek, ezért
		+	:<math>\int\limits_{|z|=1}\frac{1}{z^2}\,\mathrm{d}z=0</math>
		+	hiszen zárt a görbe, azaz a pr. fv. a kezdő és végpontban ugyanannyi.
		+	''Bizonyitas.'' A vonalintegralra vonatkozo Newton--Leibniz-tetel (I. gradiens tetel) a kovetkezo. G vegpontjai: a es b.
		+	:<math>\int\limits_{G}\mathrm{grad}\,\Phi\mathrm{d}\mathbf{r}=\Phi(b)-\Phi(a)</math>
−	'''3. Feladat.'''	+	:<math>\int\limits_{G}f(z)\mathrm{d}z = \int\limits_{G} u\mathrm{d}x-v\mathrm{d }y + i\int\limits_{G} u\mathrm{d}y+v\mathrm{d }x=</math>
−	:<math>\left(\frac{n+i}{n}\right)^n\to ?</math>	+	:<math>=\int\limits_{G} u\mathrm{d}x-v\mathrm{d }y + i\int\limits_{G} v\mathrm{d }x+u\mathrm{d}y</math>
−	''(Útmutatás: használjunk trigonometrikus alakot és hatványozzunk.)''	+	:<math>F=\Phi+i\Psi</math>
		+	:<math>f=F'=\partial_x\Phi+i\partial_y(-\Phi)=u+vi</math>
		+	:<math>f=F'=\partial_y(\Psi)+i\partial_x(\Psi)=u+vi</math>
		+	:<math>\mathrm{grad}\,\Phi = (u,-v)</math>
		+	:<math>\mathrm{grad}\,\Psi = (v,u)</math>
−	:<math>\left(\frac{n+i}{n}\right)^n=\left(\sqrt{1+\frac{1}{n^2}}\right)^n\cdot\left(\cos\left(n\,\mathrm{arc\,tg}\left(\frac{1}{n}\right)\right)+i\sin\left(n\,\mathrm{arc\,tg}\left(\frac{1}{n}\right)\right)\right)\to </math>	+	:<math>=\int\limits_{G} u\mathrm{d}x-v\mathrm{d }y + i\int\limits_{G} v\mathrm{d }x+u\mathrm{d}y=\Phi(b)-\Phi(a)+i(\Psi(b)-\Psi(a))</math>
−	:: <math>\to \cos1+i\sin 1\,</math>	+
−	Mert a szögfüggvények argumentumában lévő sorozat az 1-hez tart (pl L'Hospital-szabállyal majd átviteli elvvel ellenőrizhető), a első szorzó pedig az 1-ehez tart (rendőrelvvel). Az argumentumokban lévő értéket tertmészetesen radiánban kell venni: nem 1˚, hanem 1 rad.	+
−	==Komplex sorok==
−	Minden normált térben definiálhatók sorok és ezek konvergenciája, így '''C'''-ben is. Az (''z''<sub>n</sub>) sorozat	+	==Cirkulációmentesség==
−	: <math>s_n=\sum\limits_{k=1}^n z_k</math>	+
−	részletösszegeinek (''s''<sub>n</sub>) sorozatát a (''z''<sub>n</sub>) -ből képzett '''sor'''nak nevezzük és &sum;(''z''<sub>n</sub>)-nel jelöljük. Azt mondjuk, hogy a &sum;(''z''<sub>n</sub>) sor konvergens és összege a ''w'' komplex szám, ha (''z''<sub>n</sub>) részletösszegeinek sorozata konvergens és határértéke ''w''. Ekkor az összeget a	+
−	:<math>\sum\limits_{n=1}^{\infty}z_n</math>	+
−	szimbólummal jelöljük.	+
−	===Komponensek===	+	'''Visszavezetés valós vonalintegrálra.'''
		+	Az integrál kifejezhető vonalintegrállal. Ha ugyanis f= u + iv, akkor az f=(u,v) vektormezőnek olyan differenciálforma szerinti integrálja a komplex pályamenti integrál, mely az f=(u,v) vektor és a dz=(dx,dy) infinitezimális elmozdulásvektor komplex szorzásaként jön létre:
		+	:<math>\int\limits_{G}f(z)\mathrm{d}z = \int\limits_{G} u\mathrm{d}x-v\mathrm{d }y + i\int\limits_{G} u\mathrm{d}y+v\mathrm{d }x</math>
		+	Ebben a felírásban az (u,-v) és (v,u) olyan segédvektormezők, melyek vonalintegráljai adják meg a komplex integrál valós és képzetes részét. Tehát az integrált a
		+	:<math>\mathbf{P}=\begin{pmatrix}u\\-v\end{pmatrix}</math> és <math>\mathbf{Q}=\begin{pmatrix}v\\u\end{pmatrix}</math>
		+	segédvektormezők síkbeli '''vonalintegráljai''', vagy a
		+	:<math>\mathbf{P}'=\begin{pmatrix}-v\\-u\end{pmatrix}</math> és <math>\mathbf{Q}'=\begin{pmatrix}u\\-v\end{pmatrix}</math>
		+	segédvektormezők síkbeli '''felületi integráljai''' szolgáltatják.
−	Az egyik módja, hogy a komplex sorok konvergenciáját visszavezessük a valósokra, ha a komponenssorozatokat vesszük:	+	Itt érdemes feleleveníteni, hogy az '''S''' = (<math>s_1</math>, <math>s_2</math>) síkvektormező felületi integrálja nem más, mint a (<math>-s_2</math>, <math>s_1</math>) vektormező vonalintegrálja (a megfelelő irányítással).
−	:<math>\sum(z_n)=\sum(x_n+iy_n)\,  </math>	+
−	esetén az összegeket elképzelve, azokból az i kiemelhető, így	+
−	:<math>\sum(z_n)=\sum(x_n)+i\sum(y_n)\, </math>	+
−	ahol az összeget és a szorzást tagonként végezzük. Ekkor egy sor ponrosan akkor konvergens, ha mindkét komponense konvergens.	+
−	===Cauchy-kritérium és abszolút konvergencia===	+	:<math>\int\limits_{F} \mathbf{S}\,\mathrm{d}\mathbf{f}=\int\limits_{''F''} s_1 \mathrm{d}y-s_2\mathrm{d}x</math>
		+	megfelelő módon irányítva az F felületet, ill ennek "F" görbe mivoltát.
−	Világos, hogy egy sor, mint részletösszegsorozat pontosan akkor konvergens, ha Cauchy-sorozat. Ez a Cauchy-kritérium sorokra.	+	(Azaz a s_2dx - s_1 dy differenciálforma integrálja. ''Differenciálforma'' -- nemes egyszerűséggel -- egy olyan kifejezése, ahol dx, dy, dz-k és egy vektormező komponensei vannak összeszorozva-összeadva.)
−	Létezik az abszolút konvergencia fogalmai is. Egy sor abszolút konvergens, ha a tagjai abszolútértékéből képezett sorozat konvergens. Igaz az, hogy egy normált tér akkor és csak akkor teljes, ha minden abszolút konvergens sor konvergens benne. (És '''C''' teljes, mert minden Cauchy-sorozat konvergál benne, ami pont annak a módja, hogy belássuk az előbbi kritériumot.) Persze az előfordul a teljes terekben is, hogy konvergens sorozatok nem lesznek abszolút konvergensek.
−	===Kritériumok az abszolút konvergenciára===	+	'''Tétel.''' Ha a ''D'' tartományon értelmezett ''f'' függvénynek van primitív függvénye, akkor a körintegrál minden a ''D''-ben haladó folytonosan differenciálható (ill. ilyenek véges összekapcsolásain) zárt görbén eltűnik:
		+	:<math>\oint f=0\,</math>
−	Az abszolút konvergencia fenti kritériumából egy sor komplex sorokra vonatkozó kritérium adódik a valósból.	+	További információhoz akkor jutunk, ha a többváltozós analízis cirkuálciómentességi feltételeit vizsgáljuk. Ehhez a vissza kell vezetni a komplex integrált a vonalintegrálra.
−	'''Tétel''' – Legyen (''z''<sub>n</sub>) komplex számsorozat.	+	Legyen ''f''(''z'') = ''f''(''x'',''y'') = ''u''(''x'',''y'') + i''v''(''x'',''y''). Ekkor ''f'' felfogható '''R'''<sup>2</sup> <math>\supset\!\to</math> '''R'''<sup>2</sup> függvényként, melynek vonalintegrálja a
−	# '''Szükséges kritérium:''' Ha  &sum;(''z''<sub>n</sub>) konvergens, akkor (''z''<sub>n</sub>) nulsorozat.	+	:<math>G:z(t)\equiv\mathbf{r}(t)=(x(t),y(t))\,</math>
−	# '''Geometriai sor:''' ha |''z''| < 1, akkor <math>\sum\limits_{(0)} (z^n)</math> konvergens és az összege:	+	vonal mentén:
−	#:<math>\sum\limits_{n=0}^\infty z^n=\frac{1}{1-z}</math>	+	:<math>\int\limits_{G}f(z)\mathrm{d}z = \int\limits_{G} u\mathrm{d}x-v\mathrm{d }y + i\int\limits_{G} u\mathrm{d}y+v\mathrm{d }x</math>
−	# '''Összehasonlító kritérium:''' ha az &sum;(''r''<sub>n</sub>) valós sor konvergens és |''z''<sub>n</sub>| ≤ ''r''<sub>n</sub> majdnem minden ''n''-re, akkor  &sum;(''z''<sub>n</sub>) abszolút konvergens (''majoráns-kritérium''). Ha az &sum;(''r''<sub>n</sub>) pozitív valós sor divergens és  ''r''<sub>n</sub> ≤ |''z''<sub>n</sub>| m.m., akkor &sum;(''z''<sub>n</sub>) divergens (''minoráns-kritérium'').	+	amiben az
−	# '''p-edik hatvány próba:''' ha ''p'' > 1  valós, akkor a <math>(\sum\limits_{1}\frac{1}{n^p})</math> valós sor konvergens.	+	:<math>\mathbf{v}=\begin{pmatrix}u\\-v\end{pmatrix}</math> és <math>\mathbf{w}=\begin{pmatrix}v\\u\end{pmatrix}</math>
−	#: Ha 0 ≤ ''p'' ≤ 1, akkor a <math>(\sum\limits_{1}\frac{1}{n^p})</math> valós sor divergens.	+	vektorterek integráljai szerepelnek.
−	# '''Hányadoskritérium:''' ha <math>\limsup\left|\frac{z_{n+1}}{z_n}\right|<1\,</math>, akkor &sum;(''z''<sub>n</sub>) abszolút konvergens. Ha a "liminf" > 1, akkor divergens	+
−	# '''Gyökkritérium:''' ha <math>\limsup\sqrt[n]{|z_n|}<1\,</math>, akkor  &sum;(''z''<sub>n</sub>) abszolút konvergens. Ha a "limsup" > 1, akkor divergens.	+
		+	Vagy kétdimenziós felületi integrálként:
−	'''Megjegyezzük,''' hogy ha a gyökök és hányadosok sorozata konvergál, akkor ugyanahhoz a számhoz konvergálnak.	+	:<math>\mathbf{v}'=\begin{pmatrix}-v\\-u\end{pmatrix}</math> és <math>\mathbf{w}'=\begin{pmatrix}u\\-v\end{pmatrix}</math>
		+	Ugyanis a komplex vonalintegrált síkbeli felületi integrállá lehet alakítani:
		+	:<math>\int \mathbf{v}\mathrm{d}\mathbf{A}=\int \mathbf{v}\times\mathrm{d}\mathbf{r}=\int v_1 \mathrm{d}y-v_2\mathrm{d}x</math>
−	'''4.'''
−	Konvergens-e illetve abszolút konvergens-e?
−	:<math>\sum\left(\frac{i^n}{n}\right)</math>
−	'''5.'''	+	===Green-tétel===
−	#Konvergens-e és mi a határértéke: <math>\frac{n!}{n^n}i^n</math>	+
−	#Konvergens-e <math>\sum\left(\frac{n!}{n^n}i^n\right)</math>	+
−	#Milyen ''z''-re konvergens: <math>\sum\left(\frac{n!}{n^n}z^n\right)</math>	+
−	''(Útmutatás: használjuk a hányadoskritériumot, vagy vizsgáljuk, hogy milyen rendben tartanak a végtelenhez az összetevősorozatok.)''	+	Nehany topologiai fogalom.
−	:<math>\frac{\left|\frac{(n+1)!}{(n+1)^{n+1}}i^{n+1}\right|}{\left|\frac{n!}{n^n}i^n\right|}=\frac{n+1}{\left(1+\frac{1}{n}\right)^n\cdot(n+1)}\to\frac{1}{e}<1 </math>	+	Egy ''D'' nyilt halmaz '''C'''-ben egyszeresen osszefuggo, ha benne minden zart gorbe ''pontra deformalhato''.
−	azaz 0-hoz tart-	+	Ez utobbi a kovetkezot jelenti. Azt mondjuk, hogy a &gamma;:[a,b]<math>\to</math>''D'' zart gorbe  a <math>z_0</math>  ''D''-beli pontra deformalhato a ''D'' tartomanyban, ha letezik olyan &Gamma;:[0,1]<math>\to</math> <math>D^{[a,b]}</math> gorbe erteku fuggveny, melyre &Gamma;(1)=&gamma;, &Gamma;(0)=<math>z_0</math> konstans gorbe es &Gamma; az [a,b] es <math>D^{[a,b]}</math> terek kozott hato folytonos lekepezes a szupremumnorma szerint.
		+	''Csillagszeru'' egy ''H'' halmaz '''C'''-ben, ha van olyan ''H''-beli pont ''c'' pont, hogy barmely ''H''-beli ''z'' pontra a [''cz''] szakasz ''H''-ban van.
−	'''6.'''	+	''Pelda.'' Egy csillagszeru tartomany egyszeresen osszefuggo, mert a csillagpontra valo [0,1]-beli aranyszammal parameterezett kozeppontos kicsinyites kepei alkotta parameteres gorbesereg ilyen.
−	#Konvergens-e és mi a határértéke: <math>\frac{1}{\left(1+\frac{i}{n}\right)^{n^4}}</math>	+
−	#Konvergens-e <math>\sum\left(\frac{1}{\left(1+\frac{i}{n}\right)^{n^4}}\right)</math>	+
−	#Milyen ''z''-re konvergens:<math>\sum\left(\frac{1}{\left(1+\frac{i|z|}{n}\right)^{n^4}}\right)</math>	+
−	''(Útmutatás: használjuk a gyökkritériumot.)''	+	Tetel:
−	:<math>\sqrt[n]{\left|1+\frac{i}{n}\right|^{n^4}}=\left|1+\frac{i}{n}\right|^{n^3}=\left(\sqrt{\left(1+\frac{1}{n^2}\right)^{n^2}}\right)^n\geq (1+\varepsilon)^n\to +\infty</math>	+	:<math>\int_G Pdx+Qdy=\int_D\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}dxdy</math>
−	Így a reciproka a 0-hoz tart, azaz a limszup < 1.	+
−	==Komplex hatványsorok==	+	===Gauss-tétel===
		+	Lássuk először Gauss-tételle, hogyan következtethetünk a körintegrál eltűnésére.
−	'''Definíció''' – ''Hatványsor'' – Legyen (''a''<sub>n</sub>) komplex számsorozat és ''z''<sub>0</sub> &isin; '''C'''. Ekkor az  &sum;(''a''<sub>n(</sub>id<sub>'''C'''</sub>-z<sub>0</sub>)<sup>n</sup>) függvénysort hatványsornak nevezzük és összegét, az	+	'''Gauss-tétel''' ('''R'''<sup>3</sup>-ra) Legyen '''v''' nyílt halmazon értelmezett C<sup>1</sup>-függvény, ''V'' egyszeresen összefüggő, mérhető térrész és legyen ennek &part;''V'' határa kifelé irányított felület. Ha ''V'' a határával együtt Dom('''v''')-ben van, akkor
−	:<math>z\mapsto \sum\limits_{n=0}^\infty a_n(z-z_0)^n</math>	+	:<math>\oint\limits_{\partial V} \mathbf{v}\;\mathrm{d}\mathbf{A}=\int\limits_{V} \mathrm{div}\,\mathbf{v}\;\mathrm{d}V</math>
−	hozzárendelési utasítással értelmezett, a {''z'' &isin; | &sum;(''a''<sub>n</sub>(z-''z''<sub>0</sub>)<sup>n</sup>) konvergál } halmazon értelmezett függvényt a hatványsor '''összegének''' nevezzük. Középpontja ''z''<sub>0</sub>, együtthatósorozata (''a''<sub>n</sub>).	+
−	A továbbiakban csak a  &sum;(''a''<sub>n</sub>z<sup>n</sup>) alakú, azaz a 0 körüli hatványsorokkal foglalkozunk (ezzel nem csorbítjuk az általánosságot, mert eltolással megkaphatjuk a többit is).	+	Az itt szereplő fogalmak közül néhányról beszélnünk kell.
−	'''Tétel''' – ''Cauchy–Hadamard-tétel'' – Ha (''a''<sub>n</sub>) komplex számsorozat, <math>c= \limsup\limits_{n}\sqrt[n]{|a_n|}</math> és	+	'''Felület.''' Legyenek a &phi;<sup>i</sup>:D<sub>i</sub> <math>\to</math> '''R'''<sup>3</sup> függvények folytonosan differenciálhatóak és injektívek int(''D''<sub>i</sub>)-n, melyek mérhető tarományok '''R'''<sup>2</sup>-ben. Ha a képeik egymásba nem nyúlók, azaz int(&phi;<sub>i</sub>(''D''<sub>i</sub>)) &cap; int(&phi;<sub>j</sub>(''D''<sub>j</sub>)) üres, ha ''i'' &ne; ''j'', és a képek uniója összefüggő halmaz, akkor U Ran(&phi;<sup>i</sup>)-t előállítottuk paraméteres felületként.
−	:<math>R=\left\{	+
−	\begin{matrix}	+
−	0,& \mathrm{ha} &c=+\infty\\	+
−	+\infty,& \mathrm{ha} & c=0\\	+
−	\frac{1}{c},& \mathrm{ha} & 0<c<+\infty	+
−	\end{matrix}	+
−	\right.</math>	+	Példaként említhetjük a kúp paraméterezését:
−	akkor  &sum;(''a''<sub>n</sub>z<sup>n</sup>) abszolút konvergens a B<sub>R</sub>(0) gömbön és divergens a  B<sub>1/R</sub>(&infin;) gömbön.	+
−	A tétel minden részletre kiterjedő bizonyítását nem végezzük el, csak utalunk rá, hogy nyilvánvaló, hogy a Cauchy-féle gyökkritériumot kell benne használni. A tételbeli ''R'' sugarat a hatványsor ''konvergenciasugarának'' nevezzük. ''R''-et másként is kiszámíthajuk. Ha azt tudjuk, a hányadoskritérium alapján, hogy	+	:<math>\mathbf{r}_1(\varphi, h)=\left\{\begin{matrix} h\sin\vartheta\cos \varphi\\ h\sin\vartheta\sin\varphi\\ h\end{matrix}\right.</math>, ha &phi; &isin; [0,2&pi;] és ''h'' &isin; [0,''H'']
−	:<math>\exists\lim\limits_{n\to \infty}\frac{|a_{n+1}|}{|a_n|}</math>	+	:<math>\mathbf{r}_2(\varphi, h)=\left\{\begin{matrix}r\cos\varphi\\r\sin\varphi \\ H\end{matrix}\right.</math>, ha &phi; &isin; [0,2&pi;] és ''r'' &isin; [0,''R'']
−	akkor létezik és ezzel egyenlő az n-edik gyökök sorozata is:	+	ahol H a kúp magassága, R az alapkörsugara, &theta; a félkúpszöge (z a tengelye, O a csúcsa). Tehát itt a paramétertartományok [0,2&pi;] &times; [0,''H''] és [0,2&pi;] &times; [0,''R''].
−	:<math>\exists\lim\limits_{n\to \infty}\sqrt[n]{|a_n|}=\lim\limits_{n\to \infty}\frac{|a_{n+1}|}{|a_n|}=\,''\,\frac{1}{R}\,''</math>	+
−	ahol az idézőjel azt jelzi, hogy a konvergenciasugár lehet végtelen vagy 0 is.	+
		+	'''C<sup>1</sup>-ség'''. Ez azért kell, mert a térfogati integrált a ''D'' paramétertartományon a
		+	:<math>\int\limits_{V} \mathrm{div}\,\mathbf{v}\;\mathrm{d}V=\int\limits_{\mathbf{r}^{-1}(V)}\mathrm{div}\,\mathbf{v}(\mathbf{r}(u,v,w))|\mathrm{J}^{\mathbf{r}}(u,v,w)|\;\mathrm{d}u\mathrm{d}v\mathrm{d}w</math>
		+	képlettel számoljuk és ahhoz, hogy ez lézetten, ahhoz pl az kell, hogy ne csak az '''r''' = '''r'''(u,v,w) legyen folytonosan diff.-ható, de a divergencia is folytonos legyen.
−	'''7. Feladat.''' Mi az alábbi hatványsorok konvergenciaköre és -sugara?	+	'''Egyszeresen összefüggő tartomány.''' A G<sub>1</sub>: [a,b] <math>\to</math> '''R'''<sup>3</sup> és a G<sub>2</sub>: [a,b] <math>\to</math> '''R'''<sup>3</sup> görbék homotópak, ha létezik olyan ''F'': [0,1] &times; [a,b] <math>\to</math> '''R'''<sup>3</sup> folytonos függvény, hogy F(0,.) &equiv; G<sub>1</sub> és F(1,.) &equiv; G<sub>2</sub>.Ez gyakorlatilag azt jelenti, hogy a G<sub>1</sub> a G<sub>2</sub>-be folytonos transzformációval átvihető. Egyszeresen összefüggő egy tartomány, ha benne minden zárt görbe homotóp a konstans görbével.
−	#<math>\sum\left((2i)^nn^3(z-i)^n\right)</math>	+
−	#<math>\sum\left(\mathrm{arc\,sin}\left(\frac{1}{n}\right)(z+1+i)^n\right)</math>	+
−	#<math>\sum\left(\frac{in^{2008}}{n!}z^n\right)</math>	+
		+	Az egyszeres összefüggőség lényeges feltétel. Gondoljunk a '''v'''('''r''') = '''r'''/''r''<sup>3</sup> vektortérre. Ennek divergenciája 0, de az origó körüli zárt gömbfelület integrálja 4&pi;.
−	'''Analitikus'''nak nevezünk egy ''f'' komplex függvényt, a ''z''<sub>0</sub> pontban, ha van olyan &delta; sugarú környezet és &sum;(''a''<sub>n</sub>(z-z<sub>0</sub>)<sup>n</sup>) hatványsor, hogy minden ''z'' &isin; B<sub>&delta;</sub>(''z''<sub>0</sub>)-ra ''f'' érelmezett, &sum;(''a''<sub>n</sub>(z-z<sub>0</sub>)<sup>n</sup>) konvergens és	+	'''Gauss-tétel''' ('''R'''<sup>2</sup>-re) Legyen D egyszeresen összefüggő, mérhető síktartomány és legyen G &equiv; '''r'''(t) ennek határát paraméterező zárt görbe. Ha '''v''' folytonosan '''R'''-differenciálható a D lezártján, akkor
−	:<math>f(z)=\sum\limits_{n=0}^{\infty}a_n(z-z_0)^n</math>	+	:<math>\oint\limits_{G} \mathbf{v}(\mathbf{r})\mathrm{d}\mathbf{A}=\int\limits_{D} \mathrm{div}\,(\mathbf{v})\mathrm{d}A</math>
−	Ezt úgy jelöljük, hogy ''f'' &isin; C<sup>&omega;</sup>(''z''<sub>0</sub>).	+
−	'''8. Feladat'''	+	Így tehát a komplex vonalintegrál kiszámításához csak a '''v''' ' és '''w''' ' felületi integrálját kell kiszámítanunk, amihez a Gauss-tétel miatt beli divergenciákat kell kiszámítanunk:
−	# Van-e olyan <math>\sum\limits_{(0)}(a_n(z-2))</math> hatványsor, mely konvergál a 0-ban, de divergál a 3-ban. Konvergál 2-ben, de divergál az 2,000001-ben?	+	:<math>\mathrm{div}\mathbf{v}'=-\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}=0</math>
−	# Igazoljuk, hogy az alábbi függvény analitikus a nullában. Mi sorfejtés a konvergenciaköre?	+	:<math>\mathrm{div}\mathbf{w}'=\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}=0</math>
−	#:<math>f(z) = \frac{1}{4+z^2} \,</math>	+	Ami, a C-R-egyenletek miatt igaz.
−	===Hatványsorok összegfüggvényének folytonossága és differenciálhatósága===	+	Innen
		+	:<math>\int\limits_{G}f(z)\mathrm{d}z=0</math>
−	'''Tétel''' – Ha (''a''<sub>n</sub>) komplex számsorozat, akkor az  &sum;(''a''<sub>n</sub>z<sup>n</sup>) hatványsor összegfüggvénye folytonos a konvergenciakör belsejében. Sőt, reguláris is ott.	+	===Stokes-tétel===
−	Emlékeztetünk arra, hogy egy függvény reguláris egy pontban, ha a pont egy környezetében mindenütt értelmezett és komplex deriválható. A tétel szerint tehát analitikus függvény reguláris. A döbbenetes azonban, hogymint később kiderül: reguláris függvény analitikus: ''f'' &isin; C<sup>&omega;</sup>(''z''<sub>0</sub>) akkor és csak akkr, ha ''f'' &isin; Reg(''z''<sub>0</sub>).	+	Nézzük meg Stokes-tétellel is a bizonyítást.
−	''Bizonyítás.'' Legyen ''z'' a konvergenciakör egy belső pontja és &Delta;''z'' olyan, hogy még ''z'' + &Delta;''z'' is a konvergenciakör belsejébe esik. Ekkor:	+	'''Stokes-tétel''' ('''R'''<sup>3</sup>-ra) Legyen a nyílt halmazon értelmezett '''v''' vektorfüggvény folytonosan differenciálható, a Dom('''v''')-beli F felület pereme legyen a szintén Dom('''v''')-beli G zárt, F-nek megfelelően irányított görbe. Ekkor
−	: <math>\sum\limits_{n=0}^{\infty}a_n(z+\Delta z)^n-\sum\limits_{n=0}^{\infty}a_nz^n=	+	:<math>\oint\limits_{G} \mathbf{v}(\mathbf{r})\mathrm{d}\mathbf{r}=\int\limits_{F} \mathrm{rot}(\mathbf{v})\mathrm{d}\mathbf{F}</math>
−	\sum\limits_{n=0}^{\infty}a_n((z+\Delta z)^n-z^n)=</math>	+
−	mert mindkét sor konvergens, ekkor algebrai azonosságokkal:	+
−	:<math>=\Delta z\sum\limits_{n=0}^{\infty}a_n\sum\limits_{k=0}^{n-1}\Delta z^{k}z^{n-1-k}</math>	+
−	vagy ha tetszik nemnulla &Delta;''z''-vel:	+
−	:<math>\frac{\sum\limits_{n=0}^{\infty}a_n(z+\Delta z)^n-\sum\limits_{n=0}^{\infty}a_nz^n}{\Delta z}=\sum\limits_{n=0}^{\infty}a_n\sum\limits_{k=0}^{n-1}\Delta z^{k}z^{n-1-k}</math>	+
−	a jobb oldalon álló sor konvergenciáját a gyökkritériummal láthatjuk be:	+
−	:<math>\left|a_n\sum\limits_{k=0}^{n-1}\Delta z^{k}z^{n-1-k}\right|\leq|a_n|\cdot n r^n</math>	+
−	ahol r olyan pozitív szám, hogy | ''z'' + &Delta;''z'' | < r < R (ez  utóbbi a hatványsor konvergenciasugára). És	+
−	:<math>\limsup\limits_{n\to \infty}\sqrt[n]{|a_n|\cdot n r^n}=\limsup\limits_{n\to \infty}\sqrt[n]{|a_n|}\cdot 1 \cdot r\leq\frac{1}{R}r<1\,</math>	+
−	Így azt kaptuk, hogy minden olyan  &Delta;''z''-re, melyre | ''z'' + &Delta;''z'' | < r, teljesül és |&Delta;''z''| <&epsilon;/(1+&sum;<sub>n</sub>|a<sub>n</sub>|nr<sup>n</sup>)=:&delta;	+
−	:<math>\left|\sum\limits_{n=0}^{\infty}a_n(z+\Delta z)^n-\sum\limits_{n=0}^{\infty}a_nz^n\right|\leq|\Delta z|\cdot \sum\limits_{n=0}^\infty|a_n|nr^n<\varepsilon.</math>	+
−	Hosszadalmasabb számolásokkal, de lényegében ugyanígy kimutatható, hogy a hatványsor összegfüggvénye komplex differenciálható is a konvergenciakör belsejében és deriváltja a formális tagonkénti deriválásal kapott sor összegfüggvényével egyenlő, tehát:	+	A térbeli cirkulációmentességre vonatkozó nevezetes tétel ezzel a tétellel kapcsoltos. Ebben az esetben, bár az egyszeres összefüggőség nincs megkötve Dom('''v''')-re vonatkozólag, előjön a következményében:
−	:<math>\left(\sum\limits_{n=0}^{\infty}a_nz^n\right)'=\sum\limits_{n=1}^{\infty}a_n n z^{n-1}</math>	+
		+	'''Következmény.''' Ha az egyszeresen összefűggő ''D'' nyílt halmazon értelmezett '''v''' vektortér folytonosan differenciálható, akkor az alábbi három kijelentés ekvivaléens egymással:
		+	# rot '''v''' eltűnik ''D''-n.
		+	# minden ''D''-ben haladó zárt görbén a '''v''' körintegrálja nulla
		+	# létezik '''v'''-nek ''D''-n potenciálja, azaz olyan &Phi; : ''D'' <math>\to</math> '''R'''<sup>3</sup> függvény, melyre grad &Phi; = '''v'''.
−	==Elemi függvények==	+	Itt az egyszeres összefüggőség azért kell, mert annyit biztosan tudunk, hogy ilyen esetben a zárt görbéhez található olyan felület, mely a tartományban halad és pereme a görbe.
−	===Hatványfüggvények===	+	'''Stokes-tétel''' ('''R'''<sup>2</sup>-re) Legyen a D síkbeli felület határán a G zárt görbe ( '''r'''(t) ). Ha '''v''' folytonosan '''R'''-differenciálható, akkor
−	A	+	:<math>\oint\limits_{G} \mathbf{v}(\mathbf{r})\mathrm{d}\mathbf{r}=\int\limits_{D} \mathrm{rot}(\mathbf{v})\mathrm{d}A</math>
−	:<math>w=z^n\,</math>	+
−	típusú függvények komplex hatványfüggvények. ''n'' &isin; '''Z''' esetén, komplex deriváltjuk kiszámítható, ''n'' &ne; -1 esetben komplex primitív függvényük is van a következő értelemben:	+
−	Mivel	+	Világos, hogy a D tartománynak egyszeresen összefüggőnek kell lennie ahhoz, hogy a G a határa legyen a D-nek. Ekkor csak a rotációt kell kiszámítanunk:
−	:<math>(z^n)'=nz^{n-1}\,</math>	+
−	ezért ''n'' &ne; -1  esetén az az ''F''(''z'') függvény, melyre <math> \scriptstyle{F'(z)=z^n}</math> nem más, mint	+
−	:<math>F(z)=\frac{z^{n+1}}{n+1}+C\,</math>	+
−	ahol C komplex konstans. ''n'' &ne; -1-re nincs primitív függvénye, mert a logaritmus nem egyértékű a komplex számok között.	+
−	Komplex vonalintegrál értelmezhető a G: [a,b] <math>\to</math> '''C''' folytonos függvény, mint görbe esetén azzal a különlegességgel, hogy a szorzás a komplex szorzás:	+	:<math>\mathrm{rot}\mathbf{v}=\frac{\partial u}{\partial y} - \left(-\frac{\partial v}{\partial x}\right)=0</math>
−	:<math>\int\limits_{G}f(z)\,\mathrm{d}z\,=_{\mathrm{def}}\lim\limits_{n \to \infty}\sum\limits_{i=1}^nf(z_i)\cdot\Delta z_i</math>	+	:<math>\mathrm{rot}\mathbf{w}=\frac{\partial v}{\partial y} - \frac{\partial u}{\partial x}=0</math>
−	Feltéve persze, hogy létezik és véges. Itt ''z''<sub>i</sub> mindig a G görbe valamely pontját jelöli, amit az [a,b] egy felosztásának osztópontjainak G általi képeiből kapunk.	+
−	Ekkor fennáll a komplex Newton-Leibniz-formula. Ha a G görbe olyan nyílt halmazban halad, melyben az ''f''-nek van primitív függvénye (egyértékű függvénye!) és ''f'' komplex integrálható, akkor ''z''<sub>1</sub> és ''z''<sub>2</sub> a végpontok esetén (''a'' és ''b'' képe), a komplex integrál kiszámítható így:	+	Ami, a C-R-egyenletek miatt igaz.
−	:<math>F(z_2)-F(z_1)=\int\limits_{G}f(z)\,\mathrm{d}z\,</math>	+
−	Ha a görbe belép az ''f'' értelmezési tartományának olyan részére, melyben a függvénynek nincs egyértelmű primitív függvénye, akkor az integrál értéke függhet a G úttól.	+	===Goursat-lemma, Cauchy-féle integráltétel===
−		+
−	'''1. Feladat.''' Legyen G a 3 középpontú, 1 sugarú kör felső félköre (pozitív irányítással). Számítsuk ki a	+
−	:<math>\int\limits_{G}3z^2+1\,\mathrm{d}z\,</math>	+
−	integrált.	+
−	'''2. Feladat.''' Legyen G az origó körüli 2 sugarú kör vonal. Mennyi az	+	Goursat ennél is mélyebb eredményt talált:
−	:a) <math>\int\limits_{G}\frac{1}{z^2}\,\mathrm{d}z\,</math> és a b) <math>\int\limits_{G}\frac{z+1}{z}\,\mathrm{d}z\,</math>	+
−	integrál.	+
−	A hatványfüggvények inverzei szintén nem egyértékű függvények.
−	===Exponenciális függvény===	+	'''Goursat-lemma'''. A T háromszöglapon reguláris ''f'' komplex függvény integrálja a háromszög határán nulla:
−	:<math>	+	:<math>\oint\limits_{\partial T}f=0\,</math>
−	e^z=_{\mathrm{def}}\sum\limits_{n=0}^{\infty}\frac{z^n}{n!}\,</math>	+
−	Ebbőkkiderül az exponenciális függvény sok tulajdonsága. Például, ha z = x + iy, akkor	+
−	:<math>e^{x+iy}=e^x\cdot e^{iy}=e^x\cdot (\cos y + i\sin y)\,</math>	+
−	Ebből rögtön következik, hogy komplex exponenciális függvény periodikus, periódusa a p = 2&pi;i:	+
−	:<math>e^{z+2\pi i}=e^z\cdot e^{2\pi i}=e^z\cdot e^0\cdot (\cos 2\pi + i\sin 2\pi)=e^z(1+0i)\,</math>	+
−	'''3. Feladat.''' Oldjuk meg az	+
−	:<math>e^z=1+i\;</math>	+
−	egyenletet!	+
−	Írjuk át 1+i-t exponenciális alakba:	+	Innen már könnyen adódik a komplex analízis főtétele, melyet először Cauchy modott ki ugyan csak folytonosan diffható komplex függvényre, de Goursat ezt megfejelte a gyengített feltételével:
−	:<math>1+i=e^{\ln \sqrt{2}}\cdot e^{i\frac{\pi}{4}}\,	+
−	</math>	+	'''Főtétel.''' Ha a ''D'' tartományon egyszeresen összefüggő tartoányon reguláris az ''f'' komplex függvény, akkor a tartományban minden zárt G görbén a függvény integrálja nulla:
−	így	+	:<math>\oint\limits_{G} f=0\,</math>
−	:<math>z=\ln\sqrt{2} +i\frac{\pi}{4}+2\pi i\,</math>	+
−		+
−	'''4. Feladat.''' Oldjuk meg az	+
−	:<math>e^{iz}+ie^{-4iz}=0\,</math>	+
−	egyenletet!	+
−		+
−	===Komplex logaritmus és a reciprok integrálja===	+
−		+
−	Tekintsük a	+
−	:<math>w=e^z\,</math>	+
−	hozzárendelést! Ha w-t exponenciális alakban írjuk, megfeleltethetjük egymásnak a z algebrai alakját w trigonometrikus alakjával:	+
−	:<math>w=re^{i\varphi}=e^{x+iy}=e^x\cdot e^{iy}\,</math>	+
−	azaz	+
−	:<math>r=e^x\,</math> és <math>\varphi= y\,</math>	+
−	Ebből is látható, hogy a fordított leképezés végtelen sok értkű, hiszen ha y<sub>1</sub> = 2&pi; + y, akkor w(x+iy)= w(x+iy<sub>1</sub> ). Ekkor a Riemann-felület egy végtelen sok Riemann-levélből áll.	+
−		+
−	'''Feladat.''' Számítsuk ki az alábbi integrálokat:	+
−	:<math>\int\limits_{G_1}\frac{1}{z}\,\mathrm{d}x</math>	+
−	:<math>\int\limits_{G_2}\frac{1}{z}\,\mathrm{d}x</math>	+
−	ahol G<sub>1</sub> az egységkör a + irányban i-től -i-ig, G<sub>2</sub> az egységkör a - irányban i-től -i-ig.	+
−		+
−	:<math>\int\limits_{i,\,(G_1)}^{-i}\frac{1}{z}\mathrm{d}z=[\mathrm{Log}(z)]_{i}^-i=\mathrm{Log}(e^{i\frac{3}{2}\pi})-\mathrm{Log}(e^{\frac{1}{2}\pi})=i\pi\,</math>	+
−		+
−	ahol Log a logaritmus főrésze, hisz a görbe a egy Rieman-levélen belül marad, míg	+
−		+
−	:<math>\int\limits_{i,\,(G_2)}^{-i}\frac{1}{z}\mathrm{d}z=[\mathrm{Log}(z)]_{i}^-i=\mathrm{Log}(e^{-i\frac{1}{2}\pi})-\mathrm{Log}(e^{\frac{1}{2}\pi})=-i\pi\,</math>	+
−		+
−	mivel itt áthalad a görbe a következő Riemann-levélre.	+
−		+
−	Más számítással:	+
−		+
−	:<math>\int\limits_{i,\,(G_1)}^{-i}\frac{1}{z}\mathrm{d}z=\int\limits_{t=\frac{\pi}{2}}^{\frac{3\pi}{2}}\frac{1}{z(t)}\cdot\frac{\mathrm{d}z(t)}{\mathrm{d}t}\,\mathrm{d}t=\int\limits_{t=\frac{\pi}{2}}^{\frac{3\pi}{2}}e^{-it}ie^{it}\mathrm{d}t=[it]_{t=\frac{\pi}{2}}^{\frac{3\pi}{2}}</math>	+
−		+
−	===Trigonometikus függvények===	+
−		+
−	:<math>\sin z=_{\mathrm{def}}\sum\limits_{n=0}^{\infty}\frac{z^{2n+1}}{(2n+1)!}\,</math>	+
−	:<math>\cos z=_{\mathrm{def}}\sum\limits_{n=0}^{\infty}\frac{z^{2n}}{(2n)!}\,</math>	+
−		+
−	Világos, hogy valós &phi;-re:	+
−	:<math>e^{i\varphi}=\cos(\varphi)+i\sin(\varphi)\,</math>	+
−		+
−	A hiperbolikus függvényekhez hasonlóan a trigonometrikus függvények is előállnak de a komplex exponenciális segítségével:	+
−		+
−	:<math>\sin z=\frac{e^{iz}-e^{-iz}}{2i}</math>	+
−	:<math>\cos z=\frac{e^{iz}+e^{-iz}}{2} </math>	+
−		+
−	'''5. Feladat.''' Igazoljuk, hogy fennáll	+
−	:<math>\sin^2 z+ \cos^2z = 1\,</math>	+
−		+
−	'''6. Feladat.''' Oldjuk meg az	+
−	:<math>\sin 4z=0\,</math>	+
−	egyenletet!	+
−		+
−	===Hiperbolikus függvények===	+
−		+
−	:<math>\mathrm{sh}\, z=\frac{e^{z}-e^{-z}}{2}</math>	+
−	:<math>\mathrm{ch}\, z=\frac{e^{z}+e^{-z}}{2} </math>	+
−		+
−	'''7. Feladat.''' Határozzuk meg az w = sh(iz) függvény valós és képzetes részét!	+
−		+
−	Mo.	+
−	:<math>\mathrm{sh}\, iz=\frac{e^{iz}-e^{-iz}}{2}</math>	+
−	'''8. Feladat.''' G az egységkör. Számítsuk ki
−	:<math>\int\limits_{(G)}\frac{e^z}{z}\mathrm{d}z\,</math>
−	:<math>\int\limits_{(G)}\frac{\sin(z)}{z^4}\mathrm{d}z\,</math>
−	Mo.
−	:<math>\int\limits_{(G)}\frac{1}{z}+1+\frac{1}{2}z+...\mathrm{d}z\,=2\pi i</math>
−	:<math>\int\limits_{(G)}\frac{1}{z^3}-\frac{1}{2z}+\frac{1}{4!}z+...\mathrm{d}z\,=-\pi i</math>
	[[Kategória:Matematika A3]]		[[Kategória:Matematika A3]]

---

A lap 2013. október 31., 12:22-kori változata

_{<Matematika A3a 2008}

Tartalomjegyzék 1 Komplex integrál 1.1 Görbék a komplex síkon 1.1.1 Példák 1.2 Komplex vonalmenti integrál 1.3 Példa 1.4 Komplex Newton--Leibniz-formula 2 Cirkulációmentesség 2.1 Green-tétel 2.2 Gauss-tétel 2.3 Stokes-tétel 2.4 Goursat-lemma, Cauchy-féle integráltétel

Komplex integrál

Görbék a komplex síkon

Ha G:[a,b]C, tz(t) folytonosan differenciálható, akkor G-t görbének nevezzük. (Esetleg a folytonos, véges sok helyen nem folytonosan differenciálható előbbi G-ket is görbéknek nevezzük.) A G görbe egyszerű, ha nem metszi át saját magát, azaz minden t₁, t₂-re, ha z(t₁) = z(t₂), akkor t₁ = t₂. G zárt, ha z(a) = z(b). A görbe t-beli irányvektorán a

komplex számot értjük.

Példák

1. Legyen t∈[a,b]-re z(t) = x(t) + iy(t) olyan, hogy x(t) = x₀ + w₁t és y(t) = y₀ + w₂t, azaz z(t) = z₀ + wt. Ekkor z(t) egy egyenes szakasz.

És ekkor:

2. Az origó középpontú R sugarú kör:

z(t) = Re^it t∈[0,2π]

És ekkor

hiszen

Komplex vonalmenti integrál

Definíció. Ha G:[a,b]C görbe és f olyan komplex függvény, melyre Ran(G)⊆Dom(f), és f folytonos, akkor belátható, hogy létezik a

határérték, mely egy speciális Riemann-közelítőösszeg határértéke. Itt a görbén kijelöltük a véges sok z_i pontot, melyek a szigorúan monoton (t_i)-khez tartoznak a z_i = z(t_i) definícióval. Ezen [z(t_i),z(t_{i + 1})] görbeszakaszokon belül felvettük tetszőlegesen a ζ_i közbülső pontokat, és a Δz_i=[z(t_i),z(t_{i + 1})] szakaszokkal elkészítettük az f(ζ_i)Δz_i komplex szorzatokat. A határérték ezek görbére vett összegének határértéke. Ez a határérték az f függvény G-re vett komplex integrálja.

Kiszámítási formula. Belátható, hogy a fenti integrál a következőkkel egyenlő:

Példa

1. Legyen G a komplex egységkör pozitívan irányítva.

Ahol a valós Newton--Leibniz-formulát alkalmaztuk a komponensfüggvényekre.

2. Legyen G a z(t)=(1+2i)t, ahol t∈[0,1].

3. Legyen G a komplex egységkör felső fele, pozitívan irányítva.

Komplex Newton--Leibniz-formula

Ha az f komplex függvény, olyan, hogy van olyan komplex differenciálható F, melyre F'=f, akkor azt mondjuk, hogy a F az f primitív függvénye.

Komplex Newton--Leibniz-formula. Ha a nyílt halmazon értelmezett f komplex függvénynek primitív függvénye az F és f folytonos, akkor minden az f értelmezési tartományában haladó G:[a,b]C görbére:

Például:

4. Legyen 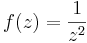. Mi az egységkörre az integrálja?

primitívfüggvénye f-nek, ezért

hiszen zárt a görbe, azaz a pr. fv. a kezdő és végpontban ugyanannyi.

Bizonyitas. A vonalintegralra vonatkozo Newton--Leibniz-tetel (I. gradiens tetel) a kovetkezo. G vegpontjai: a es b.

F = Φ + iΨ

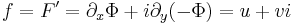
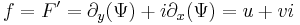
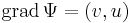
Cirkulációmentesség

Visszavezetés valós vonalintegrálra. Az integrál kifejezhető vonalintegrállal. Ha ugyanis f= u + iv, akkor az f=(u,v) vektormezőnek olyan differenciálforma szerinti integrálja a komplex pályamenti integrál, mely az f=(u,v) vektor és a dz=(dx,dy) infinitezimális elmozdulásvektor komplex szorzásaként jön létre:

Ebben a felírásban az (u,-v) és (v,u) olyan segédvektormezők, melyek vonalintegráljai adják meg a komplex integrál valós és képzetes részét. Tehát az integrált a

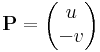és

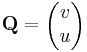
segédvektormezők síkbeli vonalintegráljai, vagy a

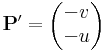és

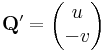
segédvektormezők síkbeli felületi integráljai szolgáltatják.

Itt érdemes feleleveníteni, hogy az S = (s₁, s₂) síkvektormező felületi integrálja nem más, mint a ( − s₂, s₁) vektormező vonalintegrálja (a megfelelő irányítással).

megfelelő módon irányítva az F felületet, ill ennek "F" görbe mivoltát.

(Azaz a s_2dx - s_1 dy differenciálforma integrálja. Differenciálforma -- nemes egyszerűséggel -- egy olyan kifejezése, ahol dx, dy, dz-k és egy vektormező komponensei vannak összeszorozva-összeadva.)

Tétel. Ha a D tartományon értelmezett f függvénynek van primitív függvénye, akkor a körintegrál minden a D-ben haladó folytonosan differenciálható (ill. ilyenek véges összekapcsolásain) zárt görbén eltűnik:

További információhoz akkor jutunk, ha a többváltozós analízis cirkuálciómentességi feltételeit vizsgáljuk. Ehhez a vissza kell vezetni a komplex integrált a vonalintegrálra.

Legyen f(z) = f(x,y) = u(x,y) + iv(x,y). Ekkor f felfogható R² R² függvényként, melynek vonalintegrálja a

vonal mentén:

amiben az

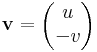és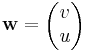

vektorterek integráljai szerepelnek.

Vagy kétdimenziós felületi integrálként:

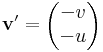és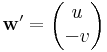

Ugyanis a komplex vonalintegrált síkbeli felületi integrállá lehet alakítani:

Green-tétel

Nehany topologiai fogalom.

Egy D nyilt halmaz C-ben egyszeresen osszefuggo, ha benne minden zart gorbe pontra deformalhato. Ez utobbi a kovetkezot jelenti. Azt mondjuk, hogy a γ:[a,b]D zart gorbe a z₀ D-beli pontra deformalhato a D tartomanyban, ha letezik olyan Γ:[0,1] D^[a,b] gorbe erteku fuggveny, melyre Γ(1)=γ, Γ(0)=z₀ konstans gorbe es Γ az [a,b] es D^[a,b] terek kozott hato folytonos lekepezes a szupremumnorma szerint.

Csillagszeru egy H halmaz C-ben, ha van olyan H-beli pont c pont, hogy barmely H-beli z pontra a [cz] szakasz H-ban van.

Pelda. Egy csillagszeru tartomany egyszeresen osszefuggo, mert a csillagpontra valo [0,1]-beli aranyszammal parameterezett kozeppontos kicsinyites kepei alkotta parameteres gorbesereg ilyen.

Tetel:

Gauss-tétel

Lássuk először Gauss-tételle, hogyan következtethetünk a körintegrál eltűnésére.

Gauss-tétel (R³-ra) Legyen v nyílt halmazon értelmezett C¹-függvény, V egyszeresen összefüggő, mérhető térrész és legyen ennek ∂V határa kifelé irányított felület. Ha V a határával együtt Dom(v)-ben van, akkor

Az itt szereplő fogalmak közül néhányról beszélnünk kell.

Felület. Legyenek a φⁱ:D_i R³ függvények folytonosan differenciálhatóak és injektívek int(D_i)-n, melyek mérhető tarományok R²-ben. Ha a képeik egymásba nem nyúlók, azaz int(φ_i(D_i)) ∩ int(φ_j(D_j)) üres, ha i ≠ j, és a képek uniója összefüggő halmaz, akkor U Ran(φⁱ)-t előállítottuk paraméteres felületként.

Példaként említhetjük a kúp paraméterezését:

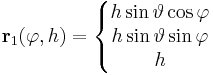, ha φ ∈ [0,2π] és h ∈ [0,H]

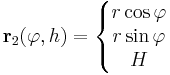, ha φ ∈ [0,2π] és r ∈ [0,R]

ahol H a kúp magassága, R az alapkörsugara, θ a félkúpszöge (z a tengelye, O a csúcsa). Tehát itt a paramétertartományok [0,2π] × [0,H] és [0,2π] × [0,R].

C¹-ség. Ez azért kell, mert a térfogati integrált a D paramétertartományon a

képlettel számoljuk és ahhoz, hogy ez lézetten, ahhoz pl az kell, hogy ne csak az r = r(u,v,w) legyen folytonosan diff.-ható, de a divergencia is folytonos legyen.

Egyszeresen összefüggő tartomány. A G₁: [a,b] R³ és a G₂: [a,b] R³ görbék homotópak, ha létezik olyan F: [0,1] × [a,b] R³ folytonos függvény, hogy F(0,.) ≡ G₁ és F(1,.) ≡ G₂.Ez gyakorlatilag azt jelenti, hogy a G₁ a G₂-be folytonos transzformációval átvihető. Egyszeresen összefüggő egy tartomány, ha benne minden zárt görbe homotóp a konstans görbével.

Az egyszeres összefüggőség lényeges feltétel. Gondoljunk a v(r) = r/r³ vektortérre. Ennek divergenciája 0, de az origó körüli zárt gömbfelület integrálja 4π.

Gauss-tétel (R²-re) Legyen D egyszeresen összefüggő, mérhető síktartomány és legyen G ≡ r(t) ennek határát paraméterező zárt görbe. Ha v folytonosan R-differenciálható a D lezártján, akkor

Így tehát a komplex vonalintegrál kiszámításához csak a v ' és w ' felületi integrálját kell kiszámítanunk, amihez a Gauss-tétel miatt beli divergenciákat kell kiszámítanunk:

Ami, a C-R-egyenletek miatt igaz.

Innen

Stokes-tétel

Nézzük meg Stokes-tétellel is a bizonyítást.

Stokes-tétel (R³-ra) Legyen a nyílt halmazon értelmezett v vektorfüggvény folytonosan differenciálható, a Dom(v)-beli F felület pereme legyen a szintén Dom(v)-beli G zárt, F-nek megfelelően irányított görbe. Ekkor

A térbeli cirkulációmentességre vonatkozó nevezetes tétel ezzel a tétellel kapcsoltos. Ebben az esetben, bár az egyszeres összefüggőség nincs megkötve Dom(v)-re vonatkozólag, előjön a következményében:

Következmény. Ha az egyszeresen összefűggő D nyílt halmazon értelmezett v vektortér folytonosan differenciálható, akkor az alábbi három kijelentés ekvivaléens egymással:

1. rot v eltűnik D-n.
2. minden D-ben haladó zárt görbén a v körintegrálja nulla
3. létezik v-nek D-n potenciálja, azaz olyan Φ : D R³ függvény, melyre grad Φ = v.

Itt az egyszeres összefüggőség azért kell, mert annyit biztosan tudunk, hogy ilyen esetben a zárt görbéhez található olyan felület, mely a tartományban halad és pereme a görbe.

Stokes-tétel (R²-re) Legyen a D síkbeli felület határán a G zárt görbe ( r(t) ). Ha v folytonosan R-differenciálható, akkor

Világos, hogy a D tartománynak egyszeresen összefüggőnek kell lennie ahhoz, hogy a G a határa legyen a D-nek. Ekkor csak a rotációt kell kiszámítanunk:

Ami, a C-R-egyenletek miatt igaz.

Goursat-lemma, Cauchy-féle integráltétel

Goursat ennél is mélyebb eredményt talált:

Goursat-lemma. A T háromszöglapon reguláris f komplex függvény integrálja a háromszög határán nulla:

Innen már könnyen adódik a komplex analízis főtétele, melyet először Cauchy modott ki ugyan csak folytonosan diffható komplex függvényre, de Goursat ezt megfejelte a gyengített feltételével:

Főtétel. Ha a D tartományon egyszeresen összefüggő tartoányon reguláris az f komplex függvény, akkor a tartományban minden zárt G görbén a függvény integrálja nulla: