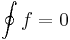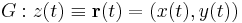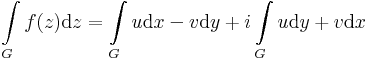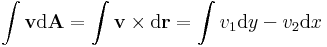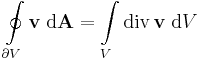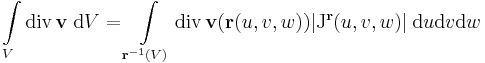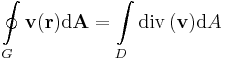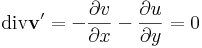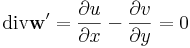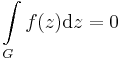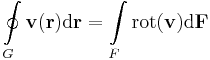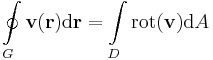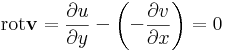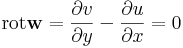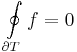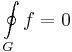Matematika A3a 2008/7. gyakorlat

_{<Matematika A3a 2008}

Cirkulációmentesség

Tétel. Ha a D tartományon értelmezett f függvénynek van primitív függvénye, akkor a körintegrál minden a D-ben haladó folytonosan differenciálható (ill. ilyenek véges összekapcsolásain) zárt görbén eltűnik:

$\oint f=0\,$

További információhoz akkor jutunk, ha a többváltozós analízis cirkuálciómentességi feltételeit vizsgáljuk. Ehhez a vissza kell vezetni a komplex integrált a vonalintegrálra.

Legyen f(z) = f(x,y) = u(x,y) + iv(x,y). Ekkor f felfogható R² 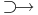$\supset\!\to$ R² függvényként, melynek vonalintegrálja a

$G:z(t)\equiv\mathbf{r}(t)=(x(t),y(t))\,$

vonal mentén:

$\int\limits_{G}f(z)\mathrm{d}z = \int\limits_{G} u\mathrm{d}x-v\mathrm{d }y + i\int\limits_{G} u\mathrm{d}y+v\mathrm{d }x$

amiben az

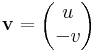$\mathbf{v}=\begin{pmatrix}u\\-v\end{pmatrix}$ és $\mathbf{w}=\begin{pmatrix}v\\u\end{pmatrix}$

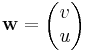
vektorterek integráljai szerepelnek.

Vagy kétdimenziós felületi integrálként:

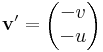$\mathbf{v}'=\begin{pmatrix}-v\\-u\end{pmatrix}$ és $\mathbf{w}'=\begin{pmatrix}u\\-v\end{pmatrix}$

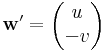
Ugyanis a komplex vonalintegrált síkbeli felületi integrállá lehet alakítani:

$\int \mathbf{v}\mathrm{d}\mathbf{A}=\int \mathbf{v}\times\mathrm{d}\mathbf{r}=\int v_1 \mathrm{d}y-v_2\mathrm{d}x$

Gauss-tétel

Lássuk először Gauss-tételle, hogyan következtethetünk a körintegrál eltűnésére.

Gauss-tétel (R³-ra) Legyen v nyílt halmazon értelmezett C¹-függvény, V egyszeresen összefüggő, mérhető térrész és legyen ennek ∂V határa kifelé irányított felület. Ha V a határával együtt Dom(v)-ben van, akkor

$\oint\limits_{\partial V} \mathbf{v}\;\mathrm{d}\mathbf{A}=\int\limits_{V} \mathrm{div}\,\mathbf{v}\;\mathrm{d}V$

Az itt szereplő fogalmak közül néhányról beszélnünk kell.

Felület. Legyenek a φⁱ:D_i $\to$ R³ függvények folytonosan differenciálhatóak és injektívek int(D_i)-n, melyek mérhető tarományok R²-ben. Ha a képeik egymásba nem nyúlók, azaz int(φ_i(D_i)) ∩ int(φ_j(D_j)) üres, ha i ≠ j, és a képek uniója összefüggő halmaz, akkor U Ran(φⁱ)-t előállítottuk paraméteres felületként.

Példaként említhetjük a kúp paraméterezését:

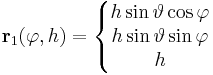$\mathbf{r}_1(\varphi, h)=\left\{\begin{matrix} h\sin\vartheta\cos \varphi\\ h\sin\vartheta\sin\varphi\\ h\end{matrix}\right.$, ha φ ∈ [0,2π] és h ∈ [0,H]

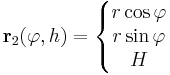$\mathbf{r}_2(\varphi, h)=\left\{\begin{matrix}r\cos\varphi\\r\sin\varphi \\ H\end{matrix}\right.$, ha φ ∈ [0,2π] és r ∈ [0,R]

ahol H a kúp magassága, R az alapkörsugara, θ a félkúpszöge (z a tengelye, O a csúcsa). Tehát itt a paramétertartományok [0,2π] × [0,H] és [0,2π] × [0,R].

C¹-ség. Ez azért kell, mert a térfogati integrált a D paramétertartományon a

$\int\limits_{V} \mathrm{div}\,\mathbf{v}\;\mathrm{d}V=\int\limits_{\mathbf{r}^{-1}(V)}\mathrm{div}\,\mathbf{v}(\mathbf{r}(u,v,w))|\mathrm{J}^{\mathbf{r}}(u,v,w)|\;\mathrm{d}u\mathrm{d}v\mathrm{d}w$

képlettel számoljuk és ahhoz, hogy ez lézetten, ahhoz pl az kell, hogy ne csak az r = r(u,v,w) legyen folytonosan diff.-ható, de a divergencia is folytonos legyen.

Egyszeresen összefüggő tartomány. A G₁: [a,b] $\to$ R³ és a G₂: [a,b] $\to$ R³ görbék homotópak, ha létezik olyan F: [0,1] × [a,b] $\to$ R³ folytonos függvény, hogy F(0,.) ≡ G₁ és F(1,.) ≡ G₂.Ez gyakorlatilag azt jelenti, hogy a G₁ a G₂-be folytonos transzformációval átvihető. Egyszeresen összefüggő egy tartomány, ha benne minden zárt görbe homotóp a konstans görbével.

Az egyszeres összefüggőség lényeges feltétel. Gondoljunk a v(r) = r/r³ vektortérre. Ennek divergenciája 0, de az origó körüli zárt gömbfelület integrálja 4π.

Gauss-tétel (R²-re) Legyen D egyszeresen összefüggő, mérhető síktartomány és legyen G ≡ r(t) ennek határát paraméterező zárt görbe. Ha v folytonosan R-differenciálható a D lezártján, akkor

$\oint\limits_{G} \mathbf{v}(\mathbf{r})\mathrm{d}\mathbf{A}=\int\limits_{D} \mathrm{div}\,(\mathbf{v})\mathrm{d}A$

Így tehát a komplex vonalintegrál kiszámításához csak a v ' és w ' felületi integrálját kell kiszámítanunk, amihez a Gauss-tétel miatt beli divergenciákat kell kiszámítanunk:

$\mathrm{div}\mathbf{v}'=-\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}=0$

$\mathrm{div}\mathbf{w}'=\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}=0$

Ami, a C-R-egyenletek miatt igaz.

Innen

$\int\limits_{G}f(z)\mathrm{d}z=0$

Stokes-tétel

Nézzük meg Stokes-tétellel is a bizonyítást.

Stokes-tétel (R³-ra) Legyen a nyílt halmazon értelmezett v vektorfüggvény folytonosan differenciálható, a Dom(v)-beli F felület pereme legyen a szintén Dom(v)-beli G zárt, F-nek megfelelően irányított görbe. Ekkor

$\oint\limits_{G} \mathbf{v}(\mathbf{r})\mathrm{d}\mathbf{r}=\int\limits_{F} \mathrm{rot}(\mathbf{v})\mathrm{d}\mathbf{F}$

A térbeli cirkulációmentességre vonatkozó nevezetes tétel ezzel a tétellel kapcsoltos. Ebben az esetben, bár az egyszeres összefüggőség nincs megkötve Dom(v)-re vonatkozólag, előjön a következményében:

Következmény. Ha az egyszeresen összefűggő D nyílt halmazon értelmezett v vektortér folytonosan differenciálható, akkor az alábbi három kijelentés ekvivaléens egymással:

1. rot v eltűnik D-n.
2. minden D-ben haladó zárt görbén a v körintegrálja nulla
3. létezik v-nek D-n potenciálja, azaz olyan Φ : D $\to$ R³ függvény, melyre grad Φ = v.

Itt az egyszeres összefüggőség azért kell, mert annyit biztosan tudunk, hogy ilyen esetben a zárt görbéhez található olyan felület, mely a tartományban halad és pereme a görbe.

Stokes-tétel (R²-re) Legyen a D síkbeli felület határán a G zárt görbe ( r(t) ). Ha v folytonosan R-differenciálható, akkor

$\oint\limits_{G} \mathbf{v}(\mathbf{r})\mathrm{d}\mathbf{r}=\int\limits_{D} \mathrm{rot}(\mathbf{v})\mathrm{d}A$

Világos, hogy a D tartománynak egyszeresen összefüggőnek kell lennie ahhoz, hogy a G a határa legyen a D-nek. Ekkor csak a rotációt kell kiszámítanunk:

$\mathrm{rot}\mathbf{v}=\frac{\partial u}{\partial y} - \left(-\frac{\partial v}{\partial x}\right)=0$

$\mathrm{rot}\mathbf{w}=\frac{\partial v}{\partial y} - \frac{\partial u}{\partial x}=0$

Ami, a C-R-egyenletek miatt igaz.

Goursat-lemma, Cauchy-féle integráltétel

Goursat ennél is mélyebb eredményt talált:

Goursat-lemma. A T háromszöglapon reguláris f komplex függvény integrálja a háromszög határán nulla:

$\oint\limits_{\partial T}f=0\,$

Innen már könnyen adódik a komplex analízis főtétele, melyet először Cauchy modott ki ugyan csak folytonosan diffható komplex függvényre, de Goursat ezt megfejelte a gyengített feltételével:

Főtétel. Ha a D tartományon egyszeresen összefüggő tartoányon reguláris az f komplex függvény, akkor a tartományban minden zárt G görbén a függvény integrálja nulla:

$\oint\limits_{G} f=0\,$