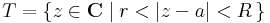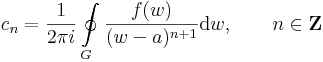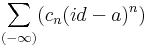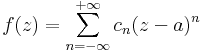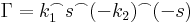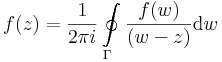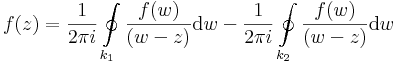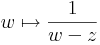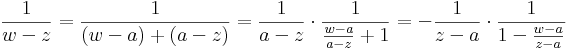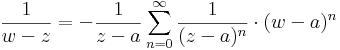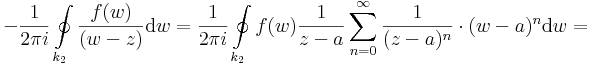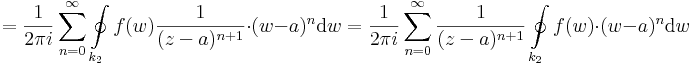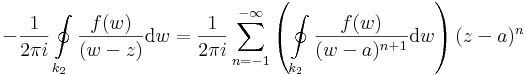Matematika A3a 2008/9. gyakorlat

A MathWikiből

(Változatok közti eltérés)

A lap 2008. december 4., 12:45-kori változata

_{<Matematika A3a 2008}

Laurent-sor

Tétel. -- A Laurent-sor tétele -- Ha az f: C 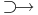$\supset\!\to$ C és a ∈ C szám és 0 ≤ r < R ≤ +∞ olyan sugarak, hogy f az

$T=\{z\in \mathbf{C}\mid r<|z-a|<R\,\}$

nyílt körgyűrűben reguláris, akkor egyértelműen léteznek olyan (c_n)_n∈Z komplex számok, éspedig tetszőleges a T-ben haladó az a-t egyszer pozitív irányban körbehurkoló G görbére:

$c_n=\frac{1}{2\pi i}\oint\limits_{G}\frac{f(w)}{(w-a)^{n+1}}\mathrm{d}w,\quad\quad n\in\mathbf{Z}$

hogy a

$\sum\limits_{(-\infty)}(c_n(id-a)^n)$

függvénysor konvergens T-ben és minden z ∈ T számra:

$f(z)=\sum\limits_{n=-\infty}^{+\infty}c_n(z-a)^n$

Bizonyítás. f-et most nem tudjuk előállítani a Cauchy-integrálformulával, mint a Taylor-sor esetén, mert az a pontban esetleg a függvény nem reguláris. De előállíthatjuk két hasonló formula különbségeként.

Rögzítsük egy tetszőlegesen választott z ∈ T-t. Legyenek k₁ és k₂ két a középpontú, T-ben haladó, pozitívan irányított kör, úgy, hogy z a k₁ és k₂ körök közötti nyílt tartományba essen. Ezekből a körökből és az őket elválasztó gyűrűt sugárirányban befelé átmetsző s szakaszból elkészítünk egy olyan zárt görbét, melyre már alkalmazható az integrálformula. Tekintsük úgy, hogy k₁ kezdő és végpontja az s kezdőpontja, k₂ kezdő és végpontja pedig az s végpontja. Legyen

$\Gamma=k_1^\frown s^\frown (-k_2)^\frown(-s)$

itt (-s) az s-sel ellenkező irányítású szakaszt jelzi. Ekkor Γ a z-t egy reguláris tartományban hurkolja egyszer, pozitívan körbe, így a Cauchy-integrálformulával:

$f(z)=\frac{1}{2\pi i}\oint\limits_{\Gamma}\frac{f(w)}{(w-z)}\mathrm{d}w$

Node, ebben az integálban az s íven kétszer oda-vissza végezzük el az integrálást, így az erre vett integrál eltűnik. Másrészt a (-k₂)-n vett integrál ellenkezője a 'k₂-vettének, így végülis:

$f(z)=\frac{1}{2\pi i}\oint\limits_{k_1}\frac{f(w)}{(w-z)}\mathrm{d}w-\frac{1}{2\pi i}\oint\limits_{k_2}\frac{f(w)}{(w-z)}\mathrm{d}w$

Hangsúlyozzuk, hogy z és a most konstansok, így a

$w\mapsto\frac{1}{w-z}\,$

az értelmezési tartományán analitikus függvény. Ennek -- szikásos módon a mértani sor összegére vonatkozó képlet segítségével -- elvégezhetjük az a középpontú, valamilyen körön belüli hatványsorba fejtését. Természetesen a |w-a| < |z-a| feltételt meg kell követelnünk, hiszen hatványsor konvergenciakörében nem lehet benne a z szakadási pont. Tegyük fel tehát, hogy |w-a| < |z-a|. Ekkor:

$\frac{1}{w-z}=\frac{1}{(w-a)+(a-z)}=\frac{1}{a-z}\cdot\frac{1}{\frac{w-a}{a-z}+1}=-\frac{1}{z-a}\cdot\frac{1}{1-\frac{w-a}{z-a}}$

Ezzel megvan a sorfejtés minden együtthatója, ugyanis 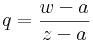$q=\frac{w-a}{z-a}$ -ra kell alkalmazni a mértani sor formuláját:

$\frac{1}{w-z}=-\frac{1}{z-a}\sum\limits_{n=0}^{\infty}\frac{1}{(z-a)^n}\cdot(w-a)^n$

1) Világos, hogy ezt a sorfejtést csak a k₂-re vonatkozó integrálban használhatjuk fel, mert ott lesz a q < 1 (ill. a w mindig közelebb a-hoz mint z-hez). Ezt az integrált tehát:

$-\frac{1}{2\pi i}\oint\limits_{k_2}\frac{f(w)}{(w-z)}\mathrm{d}w=\frac{1}{2\pi i}\oint\limits_{k_2}f(w)\frac{1}{z-a}\sum\limits_{n=0}^{\infty}\frac{1}{(z-a)^n}\cdot(w-a)^n\mathrm{d}w=$

az integrál felcserélhető a szummával és a w-től független tagok kihozhatók az integrál elé, ezért

$=\frac{1}{2\pi i}\sum\limits_{n=0}^{\infty}\oint\limits_{k_2}f(w)\frac{1}{(z-a)^{n+1}}\cdot(w-a)^n\mathrm{d}w=\frac{1}{2\pi i}\sum\limits_{n=0}^{\infty}\frac{1}{(z-a)^{n+1}}\oint\limits_{k_2}f(w)\cdot(w-a)^n\mathrm{d}w$

Ekkor egy konvergens, negatív kitevőjű hatványsort kaptunk, melynek csak főrésze van, de érdekes módon nem a középponttal és w-re, hanem a középponttal és z-ra. Ez pont a kívánt sorfejtés, melyet érdemes átindexelni úgy, hogy a szummázás -1-től induljon és -∞-ig menjen:

$-\frac{1}{2\pi i}\oint\limits_{k_2}\frac{f(w)}{(w-z)}\mathrm{d}w=\frac{1}{2\pi i}\sum\limits_{n=-1}^{-\infty}\left(\oint\limits_{k_2}\frac{f(w)}{(w-a)^{n+1}}\mathrm{d}w\right)(z-a)^{n}$

Már csak azt kell megmagyaráznunk, hogy a k₂ helyére most már minden olyan G görbére felírható, mely az a-t pozitívan öleli körbe egyszer és a regularitási tartományban halad. Valóban, a képletbeli integrál már független az 1/(w-z) sorfejtési szituációjától és minden olyan G görbére áttranszformálható melyek folytonosan áttranszformálható k₂-be. Ez a T körgyűrű összes a tételi állításban megadott görbéjére áll.

2) Most már az előző számolásból sejthető, hogy a Laurent-sor reguláris része akkor jön ki, ha az 1/(w-z) reciprokfüggvényt a az a körül nem pozitív, hanem negatív kitevőjű hatványsorba, fejtjük. Ezt a |w-a| > |z-a| feltétellel tehetjük csak meg, hisz ilyen sor konvergenciatartománya körgyűrű és a z szinguláris pontot nem tartalmazhatja.

@@ 34. sor: / 34. sor: @@
 Már csak azt kell megmagyaráznunk, hogy a ''k''<sub>2</sub> helyére most már minden olyan G görbére felírható, mely az ''a''-t pozitívan öleli körbe egyszer és a regularitási tartományban halad. Valóban, a képletbeli integrál már független az 1/(w-z) sorfejtési szituációjától és minden olyan G görbére áttranszformálható melyek folytonosan áttranszformálható ''k''<sub>2</sub>-be. Ez a ''T'' körgyűrű összes a tételi állításban megadott görbéjére áll.
+) Most már az előző számolásból sejthető, hogy a Laurent-sor reguláris része akkor jön ki, ha az 1/(w-z) reciprokfüggvényt a az ''a'' körül nem pozitív, hanem negatív kitevőjű hatványsorba, fejtjük. Ezt a  |w-a| > |z-a| feltétellel tehetjük csak meg, hisz ilyen sor konvergenciatartománya körgyűrű és a z szinguláris pontot nem tartalmazhatja.
 [[Kategória:Matematika A3]]

Matematika A3a 2008/9. gyakorlat

A lap 2008. december 4., 12:45-kori változata

Laurent-sor

Nézetek

Személyes eszközök

Navigáció

Keresés

Eszközök