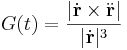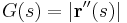Matematika A3a 2009/2. gyakorlat
A MathWikiből
A lap korábbi változatát látod, amilyen Mozo (vitalap | szerkesztései) 2009. szeptember 17., 14:39-kor történt szerkesztése után volt.
Ívhosszparaméter és görbület
A görbület adott pontban független a koordinátarendszer választásától. Ezt például az is mutatja, hogy egy általános paraméterezésben felírt értékén
túl a koordinátarendszerfüggetlen ívhosszpraméterezésben is kifejezhető a nagysága:
1. Feladat Térjünk át az alábbi görbénél ívhosszparaméterezésre és határozzuk meg a görbületet!
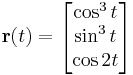 ahol
ahol ![t\in[0,2\pi]](/upload/math/1/0/e/10e9ceb4f0ea47ca0bfef8df01b9ae3b.png)
- Mo.
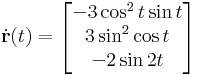 ahol
ahol ![t\in[0,2\pi]](/upload/math/1/0/e/10e9ceb4f0ea47ca0bfef8df01b9ae3b.png)