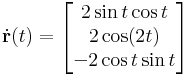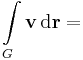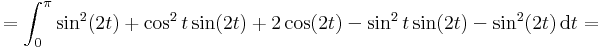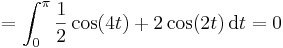Matematika A3a 2009/3. gyakorlat
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) (→Görbementi integrál) |
||
| 1. sor: | 1. sor: | ||
:''<sub>[[Matematika A3a 2009]]</sub>'' | :''<sub>[[Matematika A3a 2009]]</sub>'' | ||
==Görbementi integrál== | ==Görbementi integrál== | ||
| + | |||
| + | A '''v''' = '''v'''('''r''') vektormező integrálja az '''r''' = '''r'''(''t''), <math>t</math>=<math>t_1 ... t_2</math> görbe mentén a következő szám, ha létezik: | ||
| + | |||
| + | :<math>\int\limits_G\mathbf{v}\;\mathrm{d}r=\lim\limits_{|\Delta \mathbf{r}|\to 0,\;N\to \infty}\sum\limits_{i=1}^{N}\mathbf{v}(\mathbf{r}_i)\cdot\Delta \mathbf{r}_i</math> | ||
| + | ahol az '''r'''<sub>i</sub> pontokat a görbén "libasorban" vettük föl. | ||
| + | |||
| + | A vonalintegrál kiszámítását a következőképpen tehetjük: | ||
| + | :<math>\int\limits_{G,\mathbf{r}_1}^{\mathbf{r}_2}\mathbf{v}\;\mathrm{d}\mathbf{r}=\int\limits_{t_1}^{t_2}\mathbf{v}(\mathbf{r}(t))\cdot\dot\mathbf{r}(t)\,\mathrm{d}t</math> | ||
| + | ahol '''r'''<sub>1</sub> = '''r'''(''t''<sub>1</sub>), '''r'''<sub>2</sub> = '''r'''(''t''<sub>2</sub>). | ||
| + | |||
| + | Olyan kiszámítási mód is van, melyben nem lesz szükségünk a paraméterezésre: | ||
| + | |||
| + | :<math>\int\limits_{G}\mathbf{v}\;\mathrm{d}\mathbf{r}=\int\limits_{G}\mathbf{v}_e\,|\mathrm{d}\mathbf{r}|</math> | ||
| + | ahol '''v'''<sub>e</sub> a vektormezőnek a görbe érintője irányú komponense, az integrál pedig a vektormező ívhossz szerinti integrálja, az az integrandusban az ívhossz kiszámító képletekben egy skalárszorzót, a '''v'''<sub>e</sub>-t is szerepeltetünk. | ||
| + | |||
| + | :<math>\int\limits_{G}\mathbf{v}\;\mathrm{d}\mathbf{r}=\int\limits_{G}|\mathbf{v}|\,|\mathrm{d}\mathbf{r}_e|</math> | ||
| + | Itt a vektor mező irányú elmozdulásokat vesszük csak figyelembe. | ||
| + | |||
| + | '''1. Feladat.''' Számítsuk ki az alábbi vektormezőnek az A=(1,-2,3), B=(2,1,4) végpontú egyenes szakaszra vonatkozó integrálját! | ||
| + | |||
| + | :<math>\mathbf{v}(x,y,z)=(y+z)\mathbf{i}+(x+z)\mathbf{j}+(x+y)\mathbf{k}\,</math> | ||
| + | |||
| + | '''2. Feladat.''' Ugyannennek a vektormezőnek az | ||
| + | :<math>\mathbf{r}(t)=\sin^2 t \,\mathbf{i}+\sin(2t)\,\mathbf{j}+\cos^2 t\mathbf{k},\;t\in[0,\pi]</math> | ||
| + | görbére vett integrálját! | ||
| + | |||
| + | ''Mo.'' | ||
| + | :<math>\dot\mathbf{r}(t)=\begin{bmatrix}2\sin t\cos t\\2\cos(2t)\\-2\cos t\sin t\end{bmatrix}</math> | ||
| + | :<math>\int\limits_{G}\mathbf{v}\,\mathrm{d}\mathbf{r}=</math> | ||
| + | :<math>=\int_0^\pi\sin^2(2t)+\cos^2t\sin(2t)+2\cos(2t)-\sin^2t\sin(2t)-\sin^2(2t)\,\mathrm{d}t=</math> | ||
| + | :<math>=\int_0^\pi\frac{1}{2}\cos(4t)+2\cos(2t)\,\mathrm{d}t=0</math> | ||
| + | |||
| + | '''3. Feladat.''' Számítsuk ki a '''v''' = '''k''' × '''r''' függvénynek az R sugarú, [x,y] síkbeli origó középpontú körre vonatkozó integrálját! | ||
| + | |||
| + | '''4. Feladat.''' Számítsuk ki a '''v''' = '''k''' × '''r''' / |'''r'''| függvénynek az R sugarú, [x,y] síkbeli origó közép vetületű, M menetemelkedésű integrálját! | ||
A lap 2009. szeptember 24., 22:02-kori változata
Görbementi integrál
A v = v(r) vektormező integrálja az r = r(t), t=t1...t2 görbe mentén a következő szám, ha létezik:
ahol az ri pontokat a görbén "libasorban" vettük föl.
A vonalintegrál kiszámítását a következőképpen tehetjük:
ahol r1 = r(t1), r2 = r(t2).
Olyan kiszámítási mód is van, melyben nem lesz szükségünk a paraméterezésre:
ahol ve a vektormezőnek a görbe érintője irányú komponense, az integrál pedig a vektormező ívhossz szerinti integrálja, az az integrandusban az ívhossz kiszámító képletekben egy skalárszorzót, a ve-t is szerepeltetünk.
Itt a vektor mező irányú elmozdulásokat vesszük csak figyelembe.
1. Feladat. Számítsuk ki az alábbi vektormezőnek az A=(1,-2,3), B=(2,1,4) végpontú egyenes szakaszra vonatkozó integrálját!
2. Feladat. Ugyannennek a vektormezőnek az
görbére vett integrálját!
Mo.
3. Feladat. Számítsuk ki a v = k × r függvénynek az R sugarú, [x,y] síkbeli origó középpontú körre vonatkozó integrálját!
4. Feladat. Számítsuk ki a v = k × r / |r| függvénynek az R sugarú, [x,y] síkbeli origó közép vetületű, M menetemelkedésű integrálját!
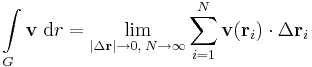
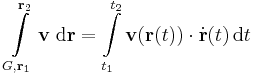
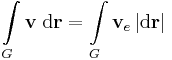
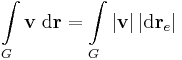
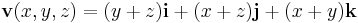
![\mathbf{r}(t)=\sin^2 t \,\mathbf{i}+\sin(2t)\,\mathbf{j}+\cos^2 t\mathbf{k},\;t\in[0,\pi]](/upload/math/5/8/8/5885f72c31f827e8807a68dd00fd46ea.png)