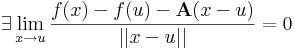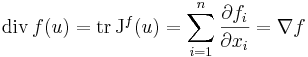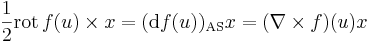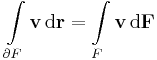Matematika A3a 2009/4. gyakorlat
A differenciáloperátor vektor és skalárinvariánsai
Az, hogy az f: Rn ⊃ Rn leképezés differenciálható az értelmezési tartományának egy u pontjában, definíció szerint azt jelenti, hogy
Rn leképezés differenciálható az értelmezési tartományának egy u pontjában, definíció szerint azt jelenti, hogy
Itt az A : Rn  Rn lineáris leképezés nem más, mint a differenciál operátor, azaz df(u). Természetesen A koordintátafüggetlen, bár egy B bázis választásával A-t mátrixként tudjuk reprezentálni. Értelmes ekkor a det(A)-t és a tr(A)-t (azaz a trace A-t) tekinteni, amik invariáns, azaz koordinátafüggetlen, csak az A-tól függő skalármenyiségek. Ezek a Szernderd bázisban a J Jacobi-mártix determinánsa és főátlójának összege. Konkrétan:
Rn lineáris leképezés nem más, mint a differenciál operátor, azaz df(u). Természetesen A koordintátafüggetlen, bár egy B bázis választásával A-t mátrixként tudjuk reprezentálni. Értelmes ekkor a det(A)-t és a tr(A)-t (azaz a trace A-t) tekinteni, amik invariáns, azaz koordinátafüggetlen, csak az A-tól függő skalármenyiségek. Ezek a Szernderd bázisban a J Jacobi-mártix determinánsa és főátlójának összege. Konkrétan:
Ha B ortonormált és csak ortonormált báziskora szorítkozunk, akkor értelmes az A transzponáltjáról, szimmetrikus és antiszimmetrikus részéről beszélni. ezen felül, ha f :R3 ⊃ R3 függvény, akkor az antiszimmertikus rész vektoriális szorzat formájában is előáll, azaz
R3 függvény, akkor az antiszimmertikus rész vektoriális szorzat formájában is előáll, azaz
ahol az első tényező a vektorinvariáns, ennek kétszerese a rotáció.
Integráltranszformációs (-redukciós) tételek
Alapséma: a Newton--Leibniz-formula. Adott az M sokaság és a sokaság ∂M pereme. Az v: M  M differenciálható függvény
M differenciálható függvény
- integrálja a határon = a derivált integrálja a peremen
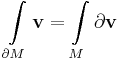
A kérdés, hogy mi a derivált.
- (1. gradiens tétel) ha M görbe, akkor ∂M két pont és ∂f = grad f,
- (Stokes-tétel) ha M felület, akkor ∂M görbe és ∂v = rot v,
- (Gauss--Osztrogradszkíj-tétel) ha M térrész, akkor ∂M felület és ∂v = div v
Stokes-tétel
1.