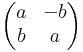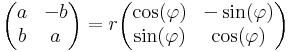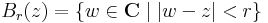Matematika A3a 2009/5. gyakorlat
Mozo (vitalap | szerkesztései) |
Mozo (vitalap | szerkesztései) (→Komplex számkör unicitása és reprezentációi) |
||
| 23. sor: | 23. sor: | ||
\sin(\varphi) & \cos(\varphi) | \sin(\varphi) & \cos(\varphi) | ||
\end{pmatrix}</math> | \end{pmatrix}</math> | ||
| + | |||
| + | ==Topológia '''C'''-ben== | ||
| + | |||
| + | '''C'''-ben, mint az '''R'''<sup>2</sup> sík elemein tehát értelmezhetjük a gömbi környezeteket, mint az '''R'''<sup>2</sup> sík pontjai körüli gömböket. Ezzel meg is kaptuk a '''C'''-beli nyílt halmazokat, azaz '''C''' topológiáját. A gömbök tehát a ''Gauss-számsík'' körlapjai: | ||
| + | :<math>B_r(z)=\{w\in \mathbf{C}\mid |w-z|< r\}</math> | ||
| + | ahol ''z'' ∈ '''C''', ''r'' > 0 valós szám. | ||
| + | |||
| + | Világos, hogy akármilyen '''R'''<sup>2</sup>-beli norma szerinti gömböket is választhattunk volna a '''C''' gömbjeinek, mert '''R'''<sup>2</sup>-ben ''minden norma ugyanazt a topológiát származtatja''. Mi a ||.||<sub>2</sub>-t, azaz az euklideszi normát emeltük ki. | ||
A lap 2009. október 15., 10:10-kori változata
Komplex számkör unicitása és reprezentációi
C, azaz a komplex számok teste kétdimenziós valós vektortér. C elemei reprezentálhatók az R2 síkon, a következő megfeleltetésekkel:
a vektortérműveletek pedig:
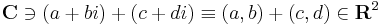vektorösszeadás (a, b, c, d ∈ R)
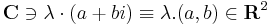valós számmal való szorzás (λ, a, b ∈ R)
A komplex számok körét a komplex szorzás tulajdonságai egyértelműsítik. C nem csak kétdimenziós valós vektortér, de a szorzással algebra is, sőt C az egyetlen kétdimenziós kommutatív, nullosztómentes valós algebra -- izomorfizmus erejéig. Sok megjelenési formája lehet a komplex számoknak, de bármely két reprezentáció olyan, hogy található olyan kölcsönösen egyértelmű leképezés köztük, mely lineáris és megtartja a szorzást is (azaz algebra izomorfizmus).
A nullosztómentesség és a kommutativitás jellemzően a mátrixalgebrákban nemtriviális tulajdonság. A komplex számok olyan lineáris leképezéseknek felelnek meg, melyek mátrixa
A komplex számok szorzása itt a mátrixszorzás.
Ezek tényleg az R2 forgatva nyújtásai, csak át kell térnünk trigonometrikus alakra:
Topológia C-ben
C-ben, mint az R2 sík elemein tehát értelmezhetjük a gömbi környezeteket, mint az R2 sík pontjai körüli gömböket. Ezzel meg is kaptuk a C-beli nyílt halmazokat, azaz C topológiáját. A gömbök tehát a Gauss-számsík körlapjai:
ahol z ∈ C, r > 0 valós szám.
Világos, hogy akármilyen R2-beli norma szerinti gömböket is választhattunk volna a C gömbjeinek, mert R2-ben minden norma ugyanazt a topológiát származtatja. Mi a ||.||2-t, azaz az euklideszi normát emeltük ki.
