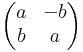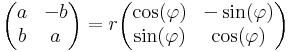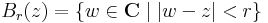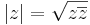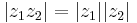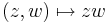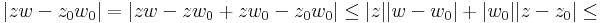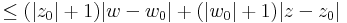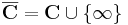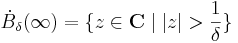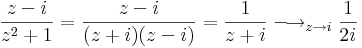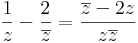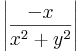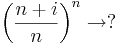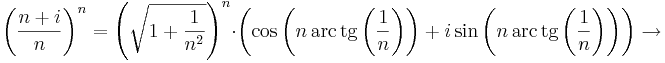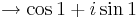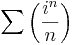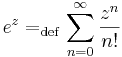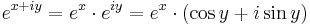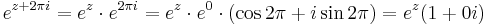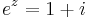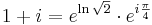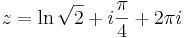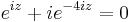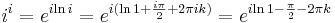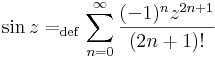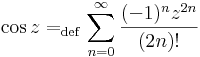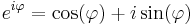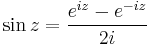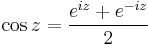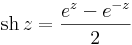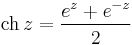Matematika A3a 2009/5. gyakorlat
Mozo (vitalap | szerkesztései) (→Topológia '''C'''-ben) |
Mozo (vitalap | szerkesztései) (→Kompaktifikáció) |
||
| (egy szerkesztő 12 közbeeső változata nincs mutatva) | |||
| 45. sor: | 45. sor: | ||
:<math>\leq(|z_0|+1)|w-w_0|+(|w_0|+1)|z-z_0|</math> | :<math>\leq(|z_0|+1)|w-w_0|+(|w_0|+1)|z-z_0|</math> | ||
ami kisebb ε, ha max{|z-<math>z_0</math>|,|w-<math>w_0</math>|}<δ=min{ε/(|<math>z_0</math>|+1),ε/(|<math>w_0</math>|+1),1} | ami kisebb ε, ha max{|z-<math>z_0</math>|,|w-<math>w_0</math>|}<δ=min{ε/(|<math>z_0</math>|+1),ε/(|<math>w_0</math>|+1),1} | ||
| + | |||
| + | ===Kompaktifikáció=== | ||
| + | :<math>\overline{\mathbf{C}}=\mathbf{C}\cup\{\infty\}\,</math> | ||
| + | Kompaktá válik, a következő topológiával. A nyílt halmazok az '''R'''<sup>2</sup>-beli gömbök (körlapok) által meghatározott halmazok, hozzávéve a végtelen gömbi környezetei által meghatározott nyílt halmazokat. Az <math>\infty\in \overline{\mathbf{C}}</math> elem kipontozott gömbi környezetei: | ||
| + | :<math> | ||
| + | \dot{B}_{\delta}(\infty)=\{z\in \mathbf{C}\mid |z|>\frac{1}{\delta}\}</math> | ||
| + | |||
| + | Ekkor <math>\infty\in \overline{\mathbf{C}}</math> kompakt lesz. Legyen ugyanis Ω olyan nyílt halmazokból álló halmazrendszer, mely lefedi a lezártatt. Ekkor bármilyen δ-ra B<sub>δ</sub>(0) lezártja kompakt és így véges sokkal az Ω-ból lefedhető. Most vegyünk egy olyan U ∈ Ω-t, mely lefedi ∞-t. Van egy olyan B<sub>δ</sub>(∞) ⊆ környezet, mely feledi &infint;, a komplementert pedig már véges sok is lefedi. | ||
| + | |||
| + | ===Határérték=== | ||
| + | '''1.''' | ||
| + | :<math>\lim\limits_{z\to i}\frac{z-i}{z^2+1}</math> | ||
| + | |||
| + | :<math>\frac{z-i}{z^2+1}=\frac{z-i}{(z+i)(z-i)}=\frac{1}{z+i}\longrightarrow_{z\to i}\frac{1}{2i}</math> | ||
| + | '''2.''' | ||
| + | :<math>\lim\limits_{z\to 0}\frac{1}{z}-\frac{2}{\overline{z}}=?</math>, | ||
| + | |||
| + | :<math>\frac{1}{z}-\frac{2}{\overline{z}}=\frac{\overline{z}-2z}{z\overline{z}}</math> | ||
| + | csak a valós részt nézve: | ||
| + | :<math>\left|\frac{-x}{x^2+y^2}\right|</math> | ||
| + | az (x,y)=(x,0) esetben a (0,0)-hoz tartva: végtelen, de (x,y)=(0,y), akkor 0. tehát nincs. | ||
| + | |||
| + | ==Sorozatok, sorok== | ||
| + | |||
| + | '''1. ''' | ||
| + | :<math>\left(\frac{n+i}{n}\right)^n\to ?</math> | ||
| + | |||
| + | :<math>\left(\frac{n+i}{n}\right)^n=\left(\sqrt{1+\frac{1}{n^2}}\right)^n\cdot\left(\cos\left(n\,\mathrm{arc\,tg}\left(\frac{1}{n}\right)\right)+i\sin\left(n\,\mathrm{arc\,tg}\left(\frac{1}{n}\right)\right)\right)\to </math> | ||
| + | :: <math>\to \cos1+i\sin 1\,</math> | ||
| + | Mert a szögfüggvények argumentumában lévő sorozat az 1-hez tart (pl L'Hospital-szabállyal majd átviteli elvvel ellenőrizhető), a első szorzó pedig az 1-ehez tart (rendőrelvvel). | ||
| + | |||
| + | '''2.''' | ||
| + | Konvergens-e illetve abszolút konvergens-e? | ||
| + | :<math>\sum\left(\frac{i^n}{n}\right)</math> | ||
| + | |||
| + | ==Elemi függvények== | ||
| + | ===Exponenciális függvény=== | ||
| + | :<math> | ||
| + | e^z=_{\mathrm{def}}\sum\limits_{n=0}^{\infty}\frac{z^n}{n!}\,</math> | ||
| + | Ebbőkkiderül az exponenciális függvény sok tulajdonsága. Például, ha z = x + iy, akkor | ||
| + | :<math>e^{x+iy}=e^x\cdot e^{iy}=e^x\cdot (\cos y + i\sin y)\,</math> | ||
| + | Ebből rögtön következik, hogy komplex exponenciális függvény periodikus, periódusa a p = 2πi: | ||
| + | :<math>e^{z+2\pi i}=e^z\cdot e^{2\pi i}=e^z\cdot e^0\cdot (\cos 2\pi + i\sin 2\pi)=e^z(1+0i)\,</math> | ||
| + | '''Feladat.''' Oldjuk meg az | ||
| + | :<math>e^z=1+i\;</math> | ||
| + | egyenletet! | ||
| + | |||
| + | Írjuk át 1+i-t exponenciális alakba: | ||
| + | :<math>1+i=e^{\ln \sqrt{2}}\cdot e^{i\frac{\pi}{4}}\, | ||
| + | </math> | ||
| + | így | ||
| + | :<math>z=\ln\sqrt{2} +i\frac{\pi}{4}+2\pi i\,</math> | ||
| + | |||
| + | '''Feladat.''' Oldjuk meg az | ||
| + | :<math>e^{iz}+ie^{-4iz}=0\,</math> | ||
| + | egyenletet! | ||
| + | |||
| + | ===Hatvány=== | ||
| + | |||
| + | :<math>i^{i}=e^{i\mathrm{ln}\,i}=e^{i(\mathrm{ln}\,1+\frac{i\pi}{2}+2\pi ik)}=e^{i\mathrm{ln}\,1-\frac{\pi}{2}-2\pi k}</math> | ||
| + | |||
| + | ===Trigonometikus függvények=== | ||
| + | |||
| + | :<math>\sin z=_{\mathrm{def}}\sum\limits_{n=0}^{\infty}\frac{(-1)^nz^{2n+1}}{(2n+1)!}\,</math> | ||
| + | :<math>\cos z=_{\mathrm{def}}\sum\limits_{n=0}^{\infty}\frac{(-1)^nz^{2n}}{(2n)!}\,</math> | ||
| + | |||
| + | Világos, hogy valós φ-re: | ||
| + | :<math>e^{i\varphi}=\cos(\varphi)+i\sin(\varphi)\,</math> | ||
| + | |||
| + | A hiperbolikus függvényekhez hasonlóan a trigonometrikus függvények is előállnak de a komplex exponenciális segítségével: | ||
| + | |||
| + | :<math>\sin z=\frac{e^{iz}-e^{-iz}}{2i}</math> | ||
| + | :<math>\cos z=\frac{e^{iz}+e^{-iz}}{2} </math> | ||
| + | |||
| + | '''Feladat.''' Oldjuk meg az | ||
| + | :<math>\sin 4z=0\,</math> ill | ||
| + | :<math>\sin z=2\,</math> | ||
| + | egyenletet! | ||
| + | |||
| + | ===Hiperbolikus függvények=== | ||
| + | |||
| + | :<math>\mathrm{sh}\, z=\frac{e^{z}-e^{-z}}{2}</math> | ||
| + | :<math>\mathrm{ch}\, z=\frac{e^{z}+e^{-z}}{2} </math> | ||
| + | |||
| + | '''Feladat.''' Határozzuk meg az w = sh(iz) függvény valós és képzetes részét! | ||
| + | |||
| + | '''Feladat.''' Igazoljuk a definiáló sorokkal, hogy sin(iz) = i sh(z) | ||
A lap jelenlegi, 2009. október 19., 22:32-kori változata
Tartalomjegyzék |
Komplex számkör unicitása és reprezentációi
C, azaz a komplex számok teste kétdimenziós valós vektortér. C elemei reprezentálhatók az R2 síkon, a következő megfeleltetésekkel:
a vektortérműveletek pedig:
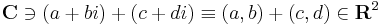 vektorösszeadás (a, b, c, d ∈ R)
vektorösszeadás (a, b, c, d ∈ R)
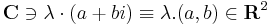 valós számmal való szorzás (λ, a, b ∈ R)
valós számmal való szorzás (λ, a, b ∈ R)
A komplex számok körét a komplex szorzás tulajdonságai egyértelműsítik. C nem csak kétdimenziós valós vektortér, de a szorzással algebra is, sőt C az egyetlen kétdimenziós kommutatív, nullosztómentes valós algebra -- izomorfizmus erejéig. Sok megjelenési formája lehet a komplex számoknak, de bármely két reprezentáció olyan, hogy található olyan kölcsönösen egyértelmű leképezés köztük, mely lineáris és megtartja a szorzást is (azaz algebra izomorfizmus).
A nullosztómentesség és a kommutativitás jellemzően a mátrixalgebrákban nemtriviális tulajdonság. A komplex számok olyan lineáris leképezéseknek felelnek meg, melyek mátrixa
A komplex számok szorzása itt a mátrixszorzás.
Ezek tényleg az R2 forgatva nyújtásai, csak át kell térnünk trigonometrikus alakra:
Topológia C-ben
C-ben, mint az R2 sík elemein tehát értelmezhetjük a gömbi környezeteket, mint az R2 sík pontjai körüli gömböket. Ezzel meg is kaptuk a C-beli nyílt halmazokat, azaz C topológiáját. A gömbök tehát a Gauss-számsík körlapjai:
ahol z ∈ C, r > 0 valós szám.
Világos, hogy akármilyen R2-beli norma szerinti gömböket is választhattunk volna a C gömbjeinek, mert R2-ben minden norma ugyanazt a topológiát származtatja. Mi a ||.||2-t, azaz az euklideszi normát emeltük ki a következő két hasznos tulajdonsága miatt:
az utóbbi azt is jelenti, hogy |.| nem csak normált algebrává teszi C-t, de ez egy abszolútérték is.
Folytonosság
A 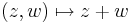 véges dimenziós valós lineáris leképezés így folytonos.
véges dimenziós valós lineáris leképezés így folytonos.
A szorzás
már nem lineáris, de még mindig folytonos:
ami kisebb ε, ha max{|z-z0|,|w-w0|}<δ=min{ε/(|z0|+1),ε/(|w0|+1),1}
Kompaktifikáció
Kompaktá válik, a következő topológiával. A nyílt halmazok az R2-beli gömbök (körlapok) által meghatározott halmazok, hozzávéve a végtelen gömbi környezetei által meghatározott nyílt halmazokat. Az 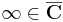 elem kipontozott gömbi környezetei:
elem kipontozott gömbi környezetei:
Ekkor 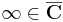 kompakt lesz. Legyen ugyanis Ω olyan nyílt halmazokból álló halmazrendszer, mely lefedi a lezártatt. Ekkor bármilyen δ-ra Bδ(0) lezártja kompakt és így véges sokkal az Ω-ból lefedhető. Most vegyünk egy olyan U ∈ Ω-t, mely lefedi ∞-t. Van egy olyan Bδ(∞) ⊆ környezet, mely feledi &infint;, a komplementert pedig már véges sok is lefedi.
kompakt lesz. Legyen ugyanis Ω olyan nyílt halmazokból álló halmazrendszer, mely lefedi a lezártatt. Ekkor bármilyen δ-ra Bδ(0) lezártja kompakt és így véges sokkal az Ω-ból lefedhető. Most vegyünk egy olyan U ∈ Ω-t, mely lefedi ∞-t. Van egy olyan Bδ(∞) ⊆ környezet, mely feledi &infint;, a komplementert pedig már véges sok is lefedi.
Határérték
1.
2.
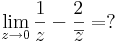 ,
,
csak a valós részt nézve:
az (x,y)=(x,0) esetben a (0,0)-hoz tartva: végtelen, de (x,y)=(0,y), akkor 0. tehát nincs.
Sorozatok, sorok
1.
Mert a szögfüggvények argumentumában lévő sorozat az 1-hez tart (pl L'Hospital-szabállyal majd átviteli elvvel ellenőrizhető), a első szorzó pedig az 1-ehez tart (rendőrelvvel).
2. Konvergens-e illetve abszolút konvergens-e?
Elemi függvények
Exponenciális függvény
Ebbőkkiderül az exponenciális függvény sok tulajdonsága. Például, ha z = x + iy, akkor
Ebből rögtön következik, hogy komplex exponenciális függvény periodikus, periódusa a p = 2πi:
Feladat. Oldjuk meg az
egyenletet!
Írjuk át 1+i-t exponenciális alakba:
így
Feladat. Oldjuk meg az
egyenletet!
Hatvány
Trigonometikus függvények
Világos, hogy valós φ-re:
A hiperbolikus függvényekhez hasonlóan a trigonometrikus függvények is előállnak de a komplex exponenciális segítségével:
Feladat. Oldjuk meg az
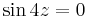 ill
ill
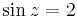
egyenletet!
Hiperbolikus függvények
Feladat. Határozzuk meg az w = sh(iz) függvény valós és képzetes részét!
Feladat. Igazoljuk a definiáló sorokkal, hogy sin(iz) = i sh(z)