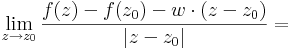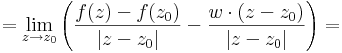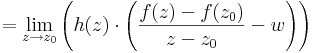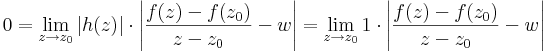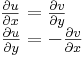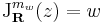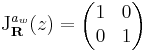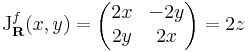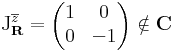Matematika A3a 2009/6. gyakorlat

A MathWikiből
(Változatok közti eltérés)
(→Példák)
(→Példák)
51. sor: 51. sor:
 
2y & 2x
 
2y & 2x
 
\end{pmatrix}=2z</math>
 
\end{pmatrix}=2z</math>
−
'''4.. ''' Számítsuk ki az  <math>\scriptstyle{f(z)=\overline{z}}</math> '''R'''-differenciálját!
+
'''4. ''' Számítsuk ki az  <math>\scriptstyle{f(z)=\overline{z}}</math> '''R'''-differenciálját!
  
 
Ha ''z'' = ''x'' + i ''y'', akkor <math>\scriptstyle{\overline{z}=x-\mathrm{i}y}</math>, így:
 
Ha ''z'' = ''x'' + i ''y'', akkor <math>\scriptstyle{\overline{z}=x-\mathrm{i}y}</math>, így:
59. sor: 59. sor:
 
\end{pmatrix}\notin\mathbf{C} </math>
 
\end{pmatrix}\notin\mathbf{C} </math>
 
tehát a konjugálás sehol sem komplex differenciálható, bár mindenhol '''R'''-differenciálható.
 
tehát a konjugálás sehol sem komplex differenciálható, bár mindenhol '''R'''-differenciálható.
 +
 +
==Elégséges feltétel==
 +
 +
Ahhoz, hogy egy ''f'' = ''u'' + i''v'' függvény komplex differenciálható legyen egy pontban, elegendő, ha
 +
# az ''u'' és a ''v'' parciálisan differenciálható a pont egy környezetében,
 +
# abban a pontban folytonosan differenciálhatók és
 +
# a Cauchy--Riemann-feltételek teljesülnek.
 +
 +
'''5.''' Hol folytonos, hol komplex differenciálható az alábbi függvény?
 +
# <math>f(z)=\overline{z}z
 +
</math>
 +
# <math>f(z)=\frac{z^3}{\overline{z}}
 +
</math>
 +
# <math>f(z)=f(x+iz)=\frac{xy}{x^2+y^2}+i\frac{xy}{x^2+y^2}
 +
</math>, ha z&ne;0 és f(0)=0

A lap 2009. október 29., 22:30-kori változata

C-differenciálhatóság

Legyen az

f(z) = f(x + iy) =u(x + iy) +iv(x + iy)

függvény

  1. valósan parciálisan deriválható z0-ban, azaz az u és v függvények legyenek parciálisan deriválhatóak az (x0,y0) pontban és
  2. tegyük fel, hogy a Jacobi-mátrixa egy w ∈ C szám mátrixreprezentációja: Jf ∈ C

(1) Ekkor egyfelől, tekintsük a totális differenciálhatóságának deifiníciójában szereplő kifejezést:

\lim\limits_{z\to z_0}\frac{f(z)-f(z_0)-w\cdot (z-z_0)}{|z-z_0|}=
=\lim\limits_{z\to z_0}\left(\frac{f(z)-f(z_0)}{|z-z_0|}-\frac{w\cdot (z-z_0)}{|z-z_0|}\right)=

Ah(z)=(z-z0)/|z-z0| függvényt kiemelve:

=\lim\limits_{z\to z_0}\left(h(z)\cdot \left(\frac{f(z)-f(z_0)}{z-z_0}-w\right)\right)

h(z) a komplex "egységgömbön" "futó" függvény, ezért hossza 1. Ha most feltesszük a komplex deriválhatóságot, azonnal kijön belőle, a korlátos x nullához tartó miatt ez a határététék 0, azaz a függvény totálisan diffható.

(2) Ha azonban a totális diffhaságot tesszük fel, akkor a |h(z)|=1 miatt:

0=\lim\limits_{z\to z_0}|h(z)|\cdot \left|\frac{f(z)-f(z_0)}{z-z_0}-w\right|=\lim\limits_{z\to z_0}1\cdot \left|\frac{f(z)-f(z_0)}{z-z_0}-w\right|

a különbdségi hányadosfüggvény abszolút értékének határértéke is nulla, de ez pont azt jelenti, hogy komplex derivált is nulla.

Tehát:

Tétel Az f = u + vi, C ⊃\to C függvénynek az z∈ Dom(f) belső pontja, akkor a következő két kijelentés ekvivalens egymással:

  1. f komplex differenciálható z-ben
  2. f totálisan R-differenciálható z-ban és
    \begin{matrix}\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}\\\;\;\;\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}\end{matrix}

ami utóbbi egyenlőség azt fejezi ki, hogy Jf ∈ C és Cauchy--Riemann-egyenleteknek nevezik őket.

Példák

1. A hozzáadás, mint affin függvény R-differenciálható, és R-differenciálja az identitás:

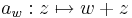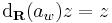
a_w:z\mapsto w+ z\, akkor \mathrm{d}_\mathbf{R}(a_w)z=z

2. A komplex számmal szorzás R-differenciálját közvetlenül a Jacobi-mátrixból számíthatjuk ki:

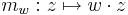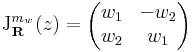
m_w:z\mapsto w\cdot z\, akkor \mathrm{J}_\mathbf{R}^{m_w}(z)=\begin{pmatrix} w_1 & -w_2\\ w_2 & w_1 \end{pmatrix}

Rendkívül érdekes észrevétel tanúi lehetünk ekkor. z \mapsto w\cdotz R-deriváltja maga w komplex számnak megfelelő mátrix, azaz

\mathrm{J}_\mathbf{R}^{m_w}(z)=w

ha mátrixreprezentációt veszünk. Sőt, visszanézve ez az összeadásra is igaz:

\mathrm{J}_\mathbf{R}^{a_w}(z)=\begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix}

3. Számítsuk ki az f(z) = z2 R-differenciálját!

Legyen z = x + i y. Ekkor z2 = x2 - y2 +i(2xy)

\mathrm{J}_\mathbf{R}^f(x,y)=\begin{pmatrix} 2x & -2y\\ 2y & 2x \end{pmatrix}=2z

4. Számítsuk ki az 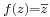\scriptstyle{f(z)=\overline{z}} R-differenciálját!

Ha z = x + i y, akkor 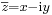\scriptstyle{\overline{z}=x-\mathrm{i}y}, így:

\mathrm{J}_\mathbf{R}^\overline{z}=\begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}\notin\mathbf{C}

tehát a konjugálás sehol sem komplex differenciálható, bár mindenhol R-differenciálható.

Elégséges feltétel

Ahhoz, hogy egy f = u + iv függvény komplex differenciálható legyen egy pontban, elegendő, ha

  1. az u és a v parciálisan differenciálható a pont egy környezetében,
  2. abban a pontban folytonosan differenciálhatók és
  3. a Cauchy--Riemann-feltételek teljesülnek.

5. Hol folytonos, hol komplex differenciálható az alábbi függvény?

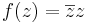
  1. f(z)=\overline{z}z
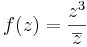
  2. f(z)=\frac{z^3}{\overline{z}}
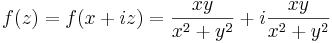  3. f(z)=f(x+iz)=\frac{xy}{x^2+y^2}+i\frac{xy}{x^2+y^2} , ha z≠0 és f(0)=0
A lap eredeti címe: „http://wiki.math.bme.hu/index.php?title=Matematika_A3a_2009/6._gyakorlat&oldid=5701”
Személyes eszközök