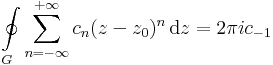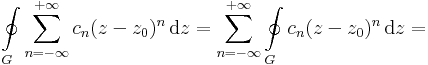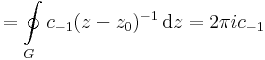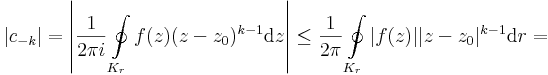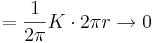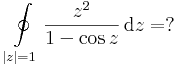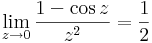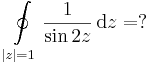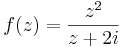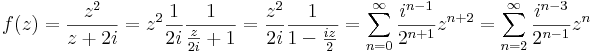Matematika A3a 2009/8. gyakorlat
Mozo (vitalap | szerkesztései) (→Egész kitevőjű hatványsor) |
Mozo (vitalap | szerkesztései) (→Egész kitevőjű hatványsor) |
||
| 43. sor: | 43. sor: | ||
:<math>1=2c_{-1} \,</math>, <math>c_{-1}=\frac{1}{2}</math> | :<math>1=2c_{-1} \,</math>, <math>c_{-1}=\frac{1}{2}</math> | ||
:<math>\oint\limits_{|z|=1}\frac{1}{\sin 2z}\,\mathrm{d}z=\pi i</math> | :<math>\oint\limits_{|z|=1}\frac{1}{\sin 2z}\,\mathrm{d}z=\pi i</math> | ||
| + | |||
| + | '''Példa.''' Adjuk meg az | ||
| + | :<math>f(z)=\frac{z^2}{z+2i}\,</math> | ||
| + | függvény azon 0 körüli Laurent-sorát, mely előállítja az 1-et! Azt is adjuk meg, mely a -3-t állítja elő! | ||
| + | |||
| + | ''Megoldás.'' -2i szinguláris hely. Ha a=0, akkor a z=1-et a 0 körüli Taylor-sor állítja elő, mert |0-1| < |0 - (-2i)|. Persze ezt is a m.s-ral adjuk meg: | ||
| + | :<math>f(z)=\frac{z^2}{z+2i}=z^2\frac{1}{2i}\frac{1}{\frac{z}{2i}+1}=\frac{z^2}{2i}\frac{1}{1-\frac{iz}{2}}=\sum\limits_{n=0}^{\infty}\frac{i^{n-1}}{2^{n+1}}z^{n+2}=\sum\limits_{n=2}^{\infty}\frac{i^{n-3}}{2^{n-1}}z^n</math> | ||
A lap 2009. november 11., 20:15-kori változata
Egész kitevőjű hatványsor
1. Feladat Igazoljuk, hogy ha ∑-∞∞cn(z − z0)n hatványsornak a z0-ban izolált szingularitása van, máshol reguláris, akkor
Mo. Ugyanis,
mert a primitív függvénnyel rendelkező tagok integráljai nullák.
2. Feladat. (Riemann-tétel) Igazoljuk, hogy ha f korlátos, z0-ban szingularis és máshol reguláris, akkor a körintegrálja eltűnik.
Mo. Belátjuk, az f Laurent-sorának főrésze eltűnik. Az Laurent-sor együtthatóformuláiból, k < 0 egészre és Kr egy 0 < r < 1 sugarú körre:
ahol K az f korlátja. Itt felhasználtuk, hogy xk − 1 < 1, ha 0 < x < 1. Ha pedig r-rel tartunk a 0-hoz, az együttható eltűnik.
f-tehát kiterjeszthető U-n reguláris függvénnyé, így a Cauchy-tétel miatt minden körintegrálja eltűnik. Vagy egyszerűbben: f reziduuma a megszüntethető szingularitási helyen 0.
3. Feladat
Mo. Megnézzük az értelmezési tartományt!
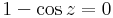 ,
, 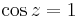 ,
,
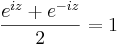
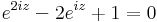
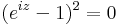
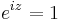
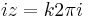 ,
, 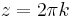
Tehát a kör lapon értelmes kivéve a 0-t, ahol viszont korlátos egy környezetben:
A maradék kompakton folytonos, így korlátos, tehát az előző tétel értelmében a körintegrálja eltűnik.
4. Feladat.
Mo. Tudjuk,
emiatt zf(z) már reguláris, ezért a Laurent-sorában a főrészben egyedül a c-1-hez tartozó tag van.
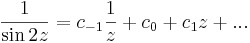
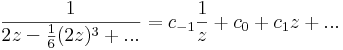
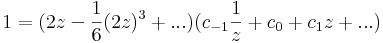
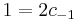 ,
, 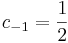
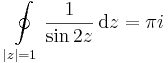
Példa. Adjuk meg az
függvény azon 0 körüli Laurent-sorát, mely előállítja az 1-et! Azt is adjuk meg, mely a -3-t állítja elő!
Megoldás. -2i szinguláris hely. Ha a=0, akkor a z=1-et a 0 körüli Taylor-sor állítja elő, mert |0-1| < |0 - (-2i)|. Persze ezt is a m.s-ral adjuk meg: