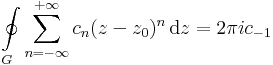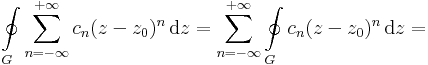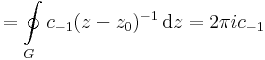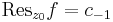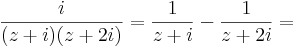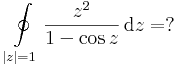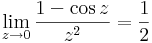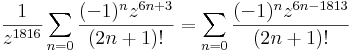Matematika A3a 2009/8. gyakorlat
Tartalomjegyzék |
Laurent-sor
1. Feladat Igazoljuk, hogy ha ∑-∞∞cn(z − z0)n hatványsornak a z0-ban izolált szingularitása van, máshol reguláris, akkor
Mo. Ugyanis,
mert a primitív függvénnyel rendelkező tagok integráljai nullák.
2. Feladat. Állítsuk elő a 3/2 i számot
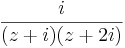 -t a 0 körül
-t a 0 körül
Mo.
Izolált szingularitások osztályozása
Ha az f a 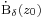 -n reguláris, de a z0-ban nem, akkor itt izolált szingularitása van. Ilyen az 1/z a 0-ban és nem ilyen a 1/sin(1/z) a 0- körül.
-n reguláris, de a z0-ban nem, akkor itt izolált szingularitása van. Ilyen az 1/z a 0-ban és nem ilyen a 1/sin(1/z) a 0- körül.
Az izolált szingularitások osztályozatók a Laurent-sora tagjai szerint.
Megszüntethető szingularitás
Ha a Laurent sor főrésze eltünik, akkor a függvény regulárissá tehető.
3. Feladat Milyen szingularitása van a 0-ban, mennyi ott a reziduuma, mennyi a körintegrálja a 0 körüli egségkörön?
Mo. Megnézzük az értelmezési tartományt!
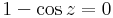 ,
, 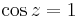 ,
,
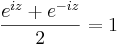
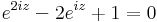
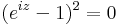
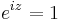
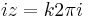 ,
, 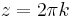
Tehát a kör lapon értelmes kivéve a 0-t, ahol viszont korlátos egy környezetben:
A maradék kompakton folytonos, így korlátos, tehát az előző tétel értelmébena körintegrálja eltűnik, a reziduuma 0, a szakadása megszüntethető.
Pólusszingularitás
Ha a Laurent-sorban az első nemnulla tag az 1/zn-hez tartozó, akkor ott a függvénynek n-edrendű pólusa van.
Persze ekkor f(z)zn már reguláris.
4. Feladat Milyen a szingularitása, mennyi a reziduuma, mennyi a körintegrálja az egysékörön a 0-ban?
- a)
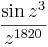
- b)
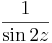
Mo.
- a)
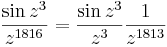
A sorból:
b) Tudjuk,
emiatt zf(z) már reguláris, ezért a Laurent-sorában a főrészben egyedül a c-1-hez tartozó tag van.
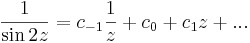
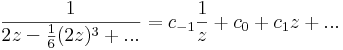
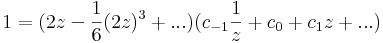
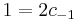 ,
, 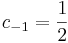
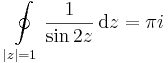
Szeparábilis differenciálegyenlet
5. Feladat
6. Feladat. Ellenőrizzük, hogy fennáll-e a Pickard-Lindelöf, a Cauchy-Peano tételek feltételei ill. hány megoldása van a y(0)=0,
egyenletnek.
7. Feladat. Ellenőrizzük, hogy fennáll-e a Pickard-Lindelöf, a Cauchy-Peano tételek feltételei ill. hány megoldása van az y(0)=0,
egyenletnek.
Házi feladatok
- Írja fel az
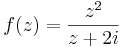
függvény azon 0 körüli Laurent-sorát, mely előállítja az 1-et! Azt is adjuk meg, mely a -3-t állítja elő!
- Írja fel az
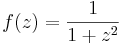 függvény 1 körüli összes Laurent-sorát!
függvény 1 körüli összes Laurent-sorát!
- Számítsa ki az
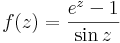 függvény 0 középponttú egységsugarú körre vett integrálját és a szakadás jellegét határozza meg.
függvény 0 középponttú egységsugarú körre vett integrálját és a szakadás jellegét határozza meg.
- Milyen szakadása van az
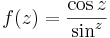 függvénynek a 0-ban és mennyi az integrálja a 0 középpontú egységkörre?
függvénynek a 0-ban és mennyi az integrálja a 0 középpontú egységkörre?
-
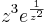 szakadásának jellege, reziduuma és inggrálja?
szakadásának jellege, reziduuma és inggrálja?